Please note that the recommended version of Scilab is 2026.0.1. This page might be outdated.
See the recommended documentation of this function
ode
ordinary differential equation solver
Calling Sequence
y = ode(y0, t0, t, f) [y, w, iw] = ode([type,] y0, t0, t [,rtol [,atol]], f [,jac] [,w, iw]) [y, rd, w, iw] = ode("root", y0, t0, t [,rtol [,atol]], f [,jac],ng, g [,w,iw]) y = ode("discrete", y0, k0, kvect, f)
Arguments
- y0
a real vector or matrix, the initial conditions.
- t0
a real scalar, the initial time.
- t
a real vector, the times at which the solution is computed.
- f
a function, external, string or list, the right hand side of the differential equation.
- type
a string, the solver to use. The available solvers are
"adams","stiff","rk","rkf","fix","discrete","roots".- rtol
a real constant or real vector of the same size as
y, the relative tolerance.- atol
a real constant or real vectors of the same size as
y, the absolute tolerance.- jac
a function, external, string or list, the Jacobian of the function
f.- w, iw
real vectors. (INPUT/OUTPUT)
- ng
an integer.
- g
an external (function or character string or list).
- k0
an integer (initial time).
- kvect
an integer vector.
- y
a real vector or matrix. (OUTPUT)
- rd
a real vector. (OUTPUT)
Description
ode solves explicit Ordinary Different Equations defined by:
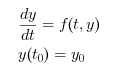
It is an interface to various solvers, in particular to ODEPACK.
In this help, we only describe the use of ode for
standard explicit ODE systems.
The simplest call of ode is:
y = ode(y0,t0,t,f) where y0 is the
vector of initial conditions, t0 is the initial
time, t is the vector of times at which the
solution y is computed and y is
matrix of solution vectors
y=[y(t(1)),y(t(2)),...].
The input argument f defines the right hand side of the
first order differential equation. This argument is a function with a specific header.
If
fis a Scilab function, its calling sequence must beydot = f(t,y)
where
tis a real scalar (the time) andyis a real vector (the state) andydotis a real vector (the first order derivative dy/dt).If
fis a string, it is the name of a Fortran subroutine or a C compiled function. For example, if we callode(y0,t0,t,"fex"), then the subroutinefexis called.The Fortran routine must have the header:
fex(n,t,y,ydot)
where
nis an integer,tis a double precision scalar,yandydotare double precision vectors.The C function must have the header:
fex(int *n,double *t,double *y,double *ydot)
where
tis the time,ythe state andydotis the state derivative (dy/dt).This external can be build in a OS independent way using ilib_for_link and dynamically linked to Scilab by the link function.
It may happen that the simulator
fneeds extra arguments. In this case, we can use the following feature. Thefargument can also be a listlst=list(simuf,u1,u2,...un)wheresimufis a Scilab function with syntax:ydot = f(t,y,u1,u2,...,un)andu1,u2, ...,unare extra arguments which are automatically passed to the simulatorsimuf.
The function f can return a p-by-q matrix instead of a vector.
With this matrix notation, we
solve the n=p+q ODE's system
dY/dt=F(t,Y) where Y is a
p x q matrix. Then initial conditions,
Y0, must also be a p x q matrix
and the result of ode is the p-by-q(T+1) matrix
[Y(t_0),Y(t_1),...,Y(t_T)].
The tolerances rtol and atol are
thresholds for relative and absolute estimated errors. The estimated
error on y(i) is:
rtol(i)*abs(y(i))+atol(i)
and integration is carried out as far as this error is small for
all components of the state. If rtol and/or
atol is a constant rtol(i)
and/or atol(i) are set to this constant value.
Default values for rtol and atol
are respectively rtol=1.d-5 and
atol=1.d-7 for most solvers and
rtol=1.d-3 and atol=1.d-4 for
"rfk" and "fix".
For stiff problems, it is better to give the Jacobian of the RHS
function as the optional argument jac.
The Jacobian is an external i.e. a function with specified syntax, or the name of a
Fortran subroutine or a C function (character string) with specified
calling sequence or a list.
If
jacis a function the syntax should beJ=jac(t,y)wheretis a real scalar (time) andya real vector (state). The result matrixJmust evaluate to df/dx i.e.J(k,i) = dfk/dxiwherefkis thek-th component off.If
jacis a character string it refers to the name of a Fortran subroutine or a C function.The Fortran routine must have the header:
subroutine fex(n,t,y,ml,mu,J,nrpd) integer n,ml,mu,nrpd double precision t,y(*),J(*)
The C function must have the header:
void fex(int *n,double *t,double *y,int *ml,int *mu,double *J,int *nrpd,)
In most cases you have not to refer
ml,muandnrpd.If
jacis a list the same conventions as forfapply.
Optional arguments w and
iw are vectors for storing information returned by
the integration routine (see ode_optional_output for details).
When these vectors are provided in RHS of ode the
integration re-starts with the same parameters as in its previous
stop.
More options can be given to ODEPACK solvers by using
%ODEOPTIONS variable. See odeoptions.
The solvers
The type of problem solved and
the method used depend on the value of the first optional argument
type which can be one of the following strings:
- <not given>:
lsodasolver of package ODEPACK is called by default. It automatically selects between nonstiff predictor-corrector Adams method and stiff Backward Differentiation Formula (BDF) method. It uses nonstiff method initially and dynamically monitors data in order to decide which method to use.- "adams":
This is for nonstiff problems.
lsodesolver of package ODEPACK is called and it uses the Adams method.- "stiff":
This is for stiff problems.
lsodesolver of package ODEPACK is called and it uses the BDF method.- "rk":
Adaptive Runge-Kutta of order 4 (RK4) method.
- "rkf":
The Shampine and Watts program based on Fehlberg's Runge-Kutta pair of order 4 and 5 (RKF45) method is used. This is for non-stiff and mildly stiff problems when derivative evaluations are inexpensive. This method should generally not be used when the user is demanding high accuracy.
- "fix":
Same solver as
"rkf", but the user interface is very simple, i.e. onlyrtolandatolparameters can be passed to the solver. This is the simplest method to try.- "root":
ODE solver with rootfinding capabilities. The
lsodarsolver of package ODEPACK is used. It is a variant of thelsodasolver where it finds the roots of a given vector function. See help on ode_root for more details.- "discrete":
Discrete time simulation. See help on ode_discrete for more details.
Examples
In the following example, we solve the Ordinary Differential Equation
dy/dt=y^2-y*sin(t)+cos(t) with the initial
condition y(0)=0.
We use the default solver.
function ydot=f(t, y) ydot=y^2-y*sin(t)+cos(t) endfunction y0=0; t0=0; t=0:0.1:%pi; y = ode(y0,t0,t,f); plot(t,y)
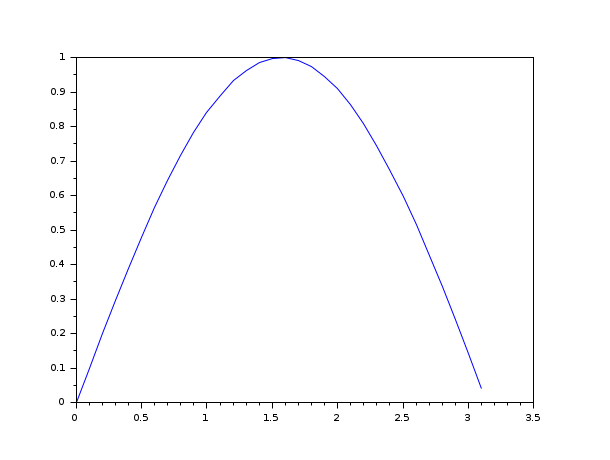
In the following example, we solve the equation dy/dt=A*y.
The exact solution is y(t)=expm(A*t)*y(0), where
expm is the matrix exponential.
The unknown is the 2-by-1 matrix y(t).
function ydot=f(t, y) ydot=A*y endfunction function J=Jacobian(t, y) J=A endfunction A=[10,0;0,-1]; y0=[0;1]; t0=0; t=1; ode("stiff",y0,t0,t,f,Jacobian) // Compare with exact solution: expm(A*t)*y0
In the following example, we solve the ODE dx/dt = A x(t) + B u(t)
with u(t)=sin(omega*t).
Notice the extra arguments of f:
A, u, B,
omega are passed to function f in a list.
function xdot=linear(t, x, A, u, B, omega) xdot=A*x+B*u(t,omega) endfunction function ut=u(t, omega) ut=sin(omega*t) endfunction A=[1 1;0 2]; B=[1;1]; omega=5; y0=[1;0]; t0=0; t=[0.1,0.2,0.5,1]; ode(y0,t0,t,list(linear,A,u,B,omega))
In the following example, we solve the Riccati differential equation
dX/dt=A'*X + X*A - X'*B*X + C where initial
condition X(0) is the 2-by-2 identity matrix.
function Xdot=ric(t, X, A, B, C) Xdot=A'*X+X*A-X'*B*X+C endfunction A=[1,1;0,2]; B=[1,0;0,1]; C=[1,0;0,1]; y0=eye(A); t0=0; t=0:0.1:%pi; X = ode(y0,t0,t,list(ric,A,B,C))
In the following example, we solve the differential equation
dY/dt=A*Y where the unknown Y(t)
is a 2-by-2 matrix.
The exact solution is Y(t)=expm(A*t), where
expm is the matrix exponential.
With a compiler
The following example requires a C compiler.
// ---------- Simple one dimension ODE (C coded external) ccode=['#include <math.h>' 'void myode(int *n,double *t,double *y,double *ydot)' '{' ' ydot[0]=y[0]*y[0]-y[0]*sin(*t)+cos(*t);' '}'] mputl(ccode,TMPDIR+'/myode.c') //create the C file // Compile ilib_for_link('myode','myode.c',[],'c',[],TMPDIR+'/loader.sce'); exec(TMPDIR+'/loader.sce') //incremental linking y0=0; t0=0; t=0:0.1:%pi; y = ode(y0,t0,t,'myode');
See Also
- ode_discrete — ordinary differential equation solver, discrete time simulation
- ode_root — ordinary differential equation solver with root finding
- dassl — differential algebraic equation
- impl — differential algebraic equation
- odedc — discrete/continuous ode solver
- odeoptions — set options for ode solvers
- csim — simulation (time response) of linear system
- ltitr — discrete time response (state space)
- rtitr — discrete time response (transfer matrix)
- intg — definite integral
Bibliography
Alan C. Hindmarsh, "lsode and lsodi, two new initial value ordinary differential equation solvers", ACM-Signum newsletter, vol. 15, no. 4 (1980), pp. 10-11.
Used Functions
The associated routines can be found in SCI/modules/differential_equations/src/fortran directory: lsode.f lsoda.f lsodar.f
| Report an issue | ||
| << numdiff | Differential calculus, Integration | ode_discrete >> |