Please note that the recommended version of Scilab is 2026.0.1. This page might be outdated.
See the recommended documentation of this function
ode
常微分方程式ソルバ
呼び出し手順
y = ode(y0, t0, t, f) [y, w, iw] = ode([type,] y0, t0, t [,rtol [,atol]], f [,jac] [,w, iw]) [y, rd, w, iw] = ode("root", y0, t0, t [,rtol [,atol]], f [,jac],ng, g [,w,iw]) y = ode("discrete", y0, k0, kvect, f)
引数
- y0
実数ベクトルまたは行列 (初期条件).
- t0
実数スカラー (初期時間).
- t
実数ベクトル (解を計算する時間).
- f
関数, 外部 ,文字列またはリスト, 微分方程式の右辺.
- type
文字列,使用するソルバ. 利用可能なソルバ:
"adams","stiff","rk","rkf","fix","discrete","roots".- rtol
実数定数または
yと同じ大きさの実数ベクトル.- atol
実数定数または
yと同じ大きさの実数ベクトル.- jac
関数, 外部 文字列またはリスト, 関数
fの ヤコビアン.- w, iw
実数ベクトル. (入力/出力)
- ng
整数.
- g
外部 (関数または文字列またはリスト).
- k0
整数 (初期時間).
- kvect
整数ベクトル.
- y
実数のベクトルまたは行列. (出力)
- rd
実数ベクトル. (出力)
説明
odeは,以下の陽の
常微分方程式を解きます:
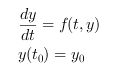
この関数は種々のソルバ, 特にODEPACKへのインターフェイスです.
このヘルプでは,
標準の陽のODEシステム用にodeの使用方法のみを
説明します.
odeの最も簡単なコールは以下のようになります:
y = ode(y0,t0,t,f)
ただし,y0 は初期条件ベクトル,
t0 は初期時間,
t は解 yを計算する時間ベクトル,
そして,yは解ベクトルの行列
y=[y(t(1)),y(t(2)),...]です.
入力ベクトルfは1次微分方程式の右辺を
定義します.
この引数は特定のヘッダを有する関数です.
fが Scilab 関数の場合, その呼び出し手順は以下のようにしますydot = f(t,y)
ただし,
tは実数スカラー(時間),yは実数ベクトル (状態量),ydotは実数ベクトル (1次微分dy/dt)です.fが文字列の場合, FortranサブルーチンまたはC関数の名前が参照されます. 例えば,ode(y0,t0,t,"fex")をコールすると, サブルーチンfexがコールされます.Fortranルーチンは以下のようなヘッダを有する必要があります:
fex(n,t,y,ydot)
ただし,
nは整数,tは 倍精度スカラー,yおよびydotは倍精度ベクトルです.C関数は以下のようなヘッダを有する必要があります:
fex(int *n,double *t,double *y,double *ydot)
ただし,
tは時間,yは 状態量,ydotは状態量の微分 (dy/dt)です.この外部ルーチンは, ilib_for_linkにより OSと独立した方法で構築でき, link 関数によりScilabに動的にリンクできます.
シミュレータ
fが他の引数を 必要とする場合も起こりえます. この場合, 以下の機能を使用可能です.fの引数を リストlst=list(simuf,u1,u2,...un)とすることも できます. ただし,simufは以下の構造を有するScilab関数です:ydot = f(t,y,u1,u2,...,un)ただし,u1,u2, ...,unは, シミュレータsimufに自動的に指定される 外部引数です.
関数fは,ベクトルではなく
p行q列の行列を返すことができます.
この行列表記により,
n=p+q次のODEシステムdY/dt=F(t,Y)
を解きます.
ただし, Yは p x qの行列です.
初期条件 Y0もp x qの行列
である必要があり, odeの結果は
p行q(T+1)列
の行列 [Y(t_0),Y(t_1),...,Y(t_T)]
となります.
許容誤差rtol および atol は
相対および絶対推定誤差の閾値です.
y(i)の指定誤差は次のようになります:
rtol(i)*abs(y(i))+atol(i)
そして,状態量の全ての要素に関してこの誤差が小さい場合,
積分が行われます.
rtolまたはatolが定数の場合,
rtol(i)またはatol(i)
はこの定数値に設定されます.
rtol および atolのデフォルト値は
多くのソルバではそれぞれrtol=1.d-5 および
atol=1.d-7,
"rfk" および "fix"では
rtol=1.d-3 および atol=1.d-4です.
スティッフな問題の場合, RHS関数のヤコビアンを
オプションの引数 jacとして
指定する方が良いでしょう.
ヤコビアンは,外部,すなわち,指定された構文を有する関数,
または指定した呼び出し手順を有するFortranサブルーチンまたは
C関数の名前(文字列),またはリストです.
jacが関数の場合, 構文はJ=jac(t,y)とする必要があります. ただし,tは実数スカラー (時間),yは実数ベクトル (状態量)です. 結果の行列Jは df/dx を評価する必要があります. ただし,J(k,i) =dfk/dxiでfkはfのk番目の要素です.jacが文字列の場合, FortranサブルーチンまたはC関数の名前を指します.このFortranルーチンは以下のようなヘッダを有する必要があります:
subroutine fex(n,t,y,ml,mu,J,nrpd) integer n,ml,mu,nrpd double precision t,y(*),J(*)
このC関数は以下のようなヘッダを有する必要があります:
void fex(int *n,double *t,double *y,int *ml,int *mu,double *J,int *nrpd,)
多くの場合,
ml,muおよびnrpdを参照する必要はありません.jacがリストの場合,fと同様の表記となります.
オプション引数wおよび
iwは,
積分ルーチンにより返される情報を
保存するベクトルです(詳細はode_optional_output 参照).
これらのベクトルが odeのRHSで提供される場合,
積分は前回の停止時と同じパラメータで再開されます.
より多くのオプションを%ODEOPTIONS変数
によりODEPACKソルバに指定することができます.
odeoptionsを参照ください.
ソルバ
解く問題の型と使用する手法は最初のオプション引数
typeの値に依存します.
この値には以下の文字列の一つを指定できます:
- <not given>:
ODEPACKパッケージの
lsodaソルバが デフォルトでコールされます. このソルバは非スティッフな問題用の予測子/修正子 Adams 法と スティッフな問題用の後退差分法(BDF)を自動的に選択します. まず非スティッフな手法が使用され,使用する手法を 決定するためにデータを動的にモニタします.- "adams":
これは非スティッフな問題用です. ODEPACKパッケージの
lsodeソルバがコールされ, この関数は Adams法を使用します.- "stiff":
これはスティッフな問題用です. ODEPACKパッケージの
lsodeソルバがコールされ, BDF法が使用されます.- "rk":
4次の適応型 Runge-Kutta (RK4) 法.
- "rkf":
Fehlbergの4次と5次の Runge-Kutta法に基づくShampine および Wattsのプログラム (RKF45) が使用されます. この方法は非スティッフおよびややスティッフな問題用で, 微係数の評価コストが低い場合に適しています. この手法は一般にユーザが高い精度を望む場合には使用するべきではありません.
- "fix":
"rkf"と同じソルバですがユーザインターフェイスが 非常にシンプルで,rtolおよびatolパラメータのみを ソルバに指定することが可能です. この手法は使用できる中で最も簡単な手法です.- "root":
解を得る機能を有するODE ソルバ. ODEPACKパッケージの
lsodarソルバが使用されます. 使用されているのはlsodaソルバを改変したもので, 指定したベクトル関数の根を見つけることができます. 詳細は ode_root のヘルプを参照してください.- "discrete":
離散時間シミュレーション. 詳細は ode_discrete のヘルプを参照してください.
例
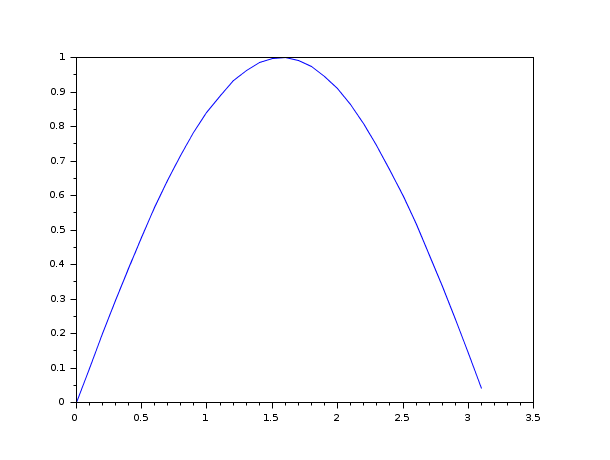
以下の例では,初期条件y(0)=0で,常微分方程式
dy/dt=y^2-y*sin(t)+cos(t)を解きます.
デフォルトのソルバを使用します.
function ydot=f(t, y) ydot=y^2-y*sin(t)+cos(t) endfunction y0=0; t0=0; t=0:0.1:%pi; y = ode(y0,t0,t,f); plot(t,y)
以下の例では,方程式dy/dt=A*yを解きます.
正確な解はy(t)=expm(A*t)*y(0)です,
ただし
expm は行列指数関数です.
未知量は2行1列の行列 y(t) です.
function ydot=f(t, y) ydot=A*y endfunction function J=Jacobian(t, y) J=A endfunction A=[10,0;0,-1]; y0=[0;1]; t0=0; t=1; ode("stiff",y0,t0,t,f,Jacobian) // Compare with exact solution: expm(A*t)*y0
以下の例では,u(t)=sin(omega*t)として,
ODE dx/dt = A x(t) + B u(t)を解きます.
外部引数 fに関する注記:
A, u, B,
omegaが関数fにリストとして
指定されます.
function xdot=linear(t, x, A, u, B, omega) xdot=A*x+B*u(t,omega) endfunction function ut=u(t, omega) ut=sin(omega*t) endfunction A=[1 1;0 2]; B=[1;1]; omega=5; y0=[1;0]; t0=0; t=[0.1,0.2,0.5,1]; ode(y0,t0,t,list(linear,A,u,B,omega))
以下の例では,リカッチ微分方程式
dX/dt=A'*X + X*A - X'*B*X + Cを解きます.
ただし,初期条件X(0)は2行2列の単位行列です.
function Xdot=ric(t, X, A, B, C) Xdot=A'*X+X*A-X'*B*X+C endfunction A=[1,1;0,2]; B=[1,0;0,1]; C=[1,0;0,1]; y0=eye(A); t0=0; t=0:0.1:%pi; X = ode(y0,t0,t,list(ric,A,B,C))
以下の例では,微分方程式
dY/dt=A*Yを解きます.
ただし,未知量Y(t)は2行2列の行列です.
厳密解は Y(t)=expm(A*t)です.
ただし,
expmは行列指数関数です.
コンパイラを使用
以下の例はCコンパイラを必要とします.
// ---------- Simple one dimension ODE (C coded external) ccode=['#include <math.h>' 'void myode(int *n,double *t,double *y,double *ydot)' '{' ' ydot[0]=y[0]*y[0]-y[0]*sin(*t)+cos(*t);' '}'] mputl(ccode,TMPDIR+'/myode.c') //create the C file // Compile ilib_for_link('myode','myode.c',[],'c',[],TMPDIR+'/loader.sce'); exec(TMPDIR+'/loader.sce') //incremental linking y0=0; t0=0; t=0:0.1:%pi; y = ode(y0,t0,t,'myode');
参照
- ode_discrete — 常微分方程式ソルバ, 離散時間シミュレーション
- ode_root — 求解付きの常微分方程式ソルバ
- dassl — 微分代数方程式
- impl — 微分代数方程式
- odedc — 離散/連続 ODE ソルバ
- odeoptions — ODEソルバのオプションを設定する
- csim — 線形システムのシミュレーション (時間応答)
- ltitr — 離散時間応答 (状態空間)
- rtitr — 離散時間応答 (伝達行列)
- intg — 定積分
参考文献
Alan C. Hindmarsh, "lsode and lsodi, two new initial value ordinary differential equation solvers", ACM-Signum newsletter, vol. 15, no. 4 (1980), pp. 10-11.
使用される関数
関連する関数は SCI/modules/differential_equations/src/fortran ディレクトリにあります: lsode.f lsoda.f lsodar.f
| Report an issue | ||
| << numdiff | Differential Equations, Integration | ode_discrete >> |