- Scilab help
- Signal Processing
- How to
- Signal
- analpf
- bilt
- buttmag
- casc
- cepstrum
- cheb1mag
- cheb2mag
- chepol
- convol
- corr
- cspect
- czt
- detrend
- dft
- ell1mag
- eqfir
- eqiir
- faurre
- ffilt
- fft
- fft2
- fftshift
- filt_sinc
- filter
- find_freq
- findm
- frfit
- frmag
- fsfirlin
- group
- hank
- hilb
- hilbert
- iir
- iirgroup
- iirlp
- intdec
- jmat
- kalm
- lattn
- lattp
- lev
- levin
- lindquist
- mese
- mfft
- mrfit
- %asn
- %k
- %sn
- phc
- pspect
- remez
- remezb
- rpem
- sincd
- srfaur
- srkf
- sskf
- syredi
- system
- trans
- wfir
- wiener
- wigner
- window
- yulewalk
- zpbutt
- zpch1
- zpch2
- zpell
Please note that the recommended version of Scilab is 2026.0.1. This page might be outdated.
See the recommended documentation of this function
fft
fast Fourier transform.
ifft
fast Fourier transform.
Calling Sequence
x=fft(a ,-1) or x=fft(a) x=fft(a,1) or x=ifft(a) x=fft(a,-1,dim,incr) x=fft(a,1,dim,incr)
Arguments
- x
real or complex vector or real or complex matrix (2-dim fft)
- a
real or complex vector or real or complex matrix (2-dim fft).
- dim
positive integer
- incr
positive integer
Description
- Short syntax
- direct
x=fft(a,-1)orx=fft(a)gives a direct transform.- single variate
If
ais a vector a single variate direct FFT is computed that is: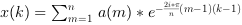
(the
-1argument refers to the sign of the exponent..., NOT to "inverse"),- multivariate
If
ais a matrix or or a multidimensionnal array a multivariate direct FFT is performed.
- inverse
a=fft(x,1)ora=ifft(x)performs the inverse transform normalized by1/n.- single variate
If
ais a vector a single variate inverse FFT is computed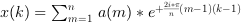
- multivariate
If
ais a matrix or or a multidimensionnal array a multivariate inverse FFT is performed.
- Long syntax for multidimensional FFT
x=fft(a,-1,dim,incr)allows to perform an multidimensional fft.If a is a real or complex vector implicitly indexed by
j1,j2,..,jpi.e.a(j1,j2,..,jp)wherej1lies in1:dim(1),j2in1:dim(2),...one gets a p-variate FFT by calling p timesfftas followsincrk=1; x=a; for k=1:p x=fft(x ,-1,dim(k),incrk) incrk=incrk*dim(k) end
where
dimkis the dimension of the current variable w.r.t which one is integrating andincrkis the increment which separates two successivejkelements ina.In particular,if
ais an mxn matrix,x=fft(a,-1)is equivalent to the two instructions:a1=fft(a,-1,m,1); x=fft(a1,-1,n,m);
Algorithms
If the fftw module has been loaded into
Scilab this function uses that library (http://www.fftw.org/). On the
other case the fft function is based on the Fortran routines fft842.f
(Cooley-Tukey algorithm for vectors of size n=2^m) and dfftbi.f (for
other sizes) .
Examples
//Frequency components of a signal //---------------------------------- // build a noides signal sampled at 1000hz containing to pure frequencies // at 50 and 70 Hz sample_rate=1000; t = 0:1/sample_rate:0.6; N=size(t,'*'); //number of samples s=sin(2*%pi*50*t)+sin(2*%pi*70*t+%pi/4)+grand(1,N,'nor',0,1); y=fft(s); //the fft response is symmetric we retain only the first N/2 points f=sample_rate*(0:(N/2))/N; //associated frequency vector n=size(f,'*') clf() plot(f,abs(y(1:n)))
//Using explicit formula for discrete Fourier transform //------------------------------------------------ function xf=DFT(x, flag); n=size(x,'*'); //Compute the n by n Fourier matrix if flag==1 then,//backward transformation am=exp(2*%pi*%i*(0:n-1)'*(0:n-1)/n); else //forward transformation am=exp(-2*%pi*%i*(0:n-1)'*(0:n-1)/n); end xf=am*matrix(x,n,1);//dft xf=matrix(xf,size(x));//reshape if flag==1 then,xf=xf/n;end endfunction //Comparison with the fast Fourier algorithm a=rand(1,1000); norm(DFT(a,1) - fft(a,1)) norm(DFT(a,-1) - fft(a,-1)) timer();DFT(a,-1);timer() timer();fft(a,-1);timer()
| << ffilt | Signal Processing | fft2 >> |