Please note that the recommended version of Scilab is 2026.0.1. This page might be outdated.
See the recommended documentation of this function
leastsq
Solves non-linear least squares problems
Calling Sequence
[fopt,[xopt,[grdopt]]]=leastsq(fun, x0) [fopt,[xopt,[grdopt]]]=leastsq(fun, dfun, x0) [fopt,[xopt,[grdopt]]]=leastsq(fun, cstr, x0) [fopt,[xopt,[grdopt]]]=leastsq(fun, dfun, cstr, x0) [fopt,[xopt,[grdopt]]]=leastsq(fun, dfun, cstr, x0, algo) [fopt,[xopt,[grdopt]]]=leastsq([imp], fun [,dfun] [,cstr],x0 [,algo],[df0,[mem]],[stop])
Arguments
- fopt
value of the function f(x)=||fun(x)||^2 at
xopt- xopt
best value of
xfound to minimize ||fun(x)||^2- grdopt
gradient of f at
xopt- fun
a scilab function or a list defining a function from R^n to R^m (see more details in DESCRIPTION).
- x0
real vector (initial guess of the variable to be minimized).
- dfun
a scilab function or a string defining the Jacobian matrix of
fun(see more details in DESCRIPTION).- cstr
bound constraints on
x. They must be introduced by the string keyword'b'followed by the lower boundbinfthen by the upper boundbsup(socstrappears as'b',binf,bsupin the calling sequence). Those bounds are real vectors with same dimension thanx0(-%inf and +%inf may be used for dimension which are unrestricted).- algo
a string with possible values:
'qn'or'gc'or'nd'. These strings stand for quasi-Newton (default), conjugate gradient or non-differentiable respectively. Note that'nd'does not accept bounds onx.- imp
scalar argument used to set the trace mode.
imp=0nothing (except errors) is reported,imp=1initial and final reports,imp=2adds a report per iteration,imp>2add reports on linear search. Warning, most of these reports are written on the Scilab standard output.- df0
real scalar. Guessed decreasing of ||fun||^2 at first iteration. (
df0=1is the default value).- mem
integer, number of variables used to approximate the Hessean (second derivatives) of f when
algo='qn'. Default value is around 6.- stop
sequence of optional parameters controlling the convergence of the algorithm. They are introduced by the keyword
'ar', the sequence being of the form'ar',nap, [iter [,epsg [,epsf [,epsx]]]]- nap
maximum number of calls to
funallowed.- iter
maximum number of iterations allowed.
- epsg
threshold on gradient norm.
- epsf
threshold controlling decreasing of
f- epsx
threshold controlling variation of
x. This vector (possibly matrix) of same size asx0can be used to scalex.
Description
fun being a function from R^n to R^m this routine tries to minimize w.r.t. x, the function:
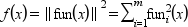
which is the sum of the squares of the components of
fun. Bound constraints may be imposed on
x.
How to provide fun and dfun
fun can be either a usual scilab function (case
1) or a fortran or a C routine linked to scilab (case 2). For most
problems the definition of fun will need
supplementary parameters and this can be done in both cases.
- case 1:
when
funis a Scilab function, its calling sequence must be:y=fun(x [,opt_par1,opt_par2,...]). Whenfunneeds optional parameters it must appear aslist(fun,opt_par1,opt_par2,...)in the calling sequence ofleastsq.- case 2:
when
funis defined by a Fortran or C routine it must appear aslist(fun_name,m [,opt_par1,opt_par2,...])in the calling sequence ofleastsq,fun_name(a string) being the name of the routine which must be linked to Scilab (see link). The generic calling sequences for this routine are:In Fortran: subroutine fun(m, n, x, params, y) integer m,n double precision x(n), params(*), y(m) In C: void fun(int *m, int *n, double *x, double *params, double *y)
where
nis the dimension of vectorx,mthe dimension of vectory(which must store the evaluation of fun at x) andparamsis a vector which contains the optional parameters opt_par1, opt_par2, ... (each parameter may be a vector, for instance if opt_par1 has 3 components, the description of opt_par2 begin fromparams(4)(fortran case), and fromparams[3](C case), etc... Note that even iffundoes not need supplementary parameters you must anyway write the fortran code with aparamsargument (which is then unused in the subroutine core).
In many cases it is adviced to provide the Jacobian matrix
dfun (dfun(i,j)=dfi/dxj) to the
optimizer (which uses a finite difference approximation otherwise) and as
for fun it may be given as a usual scilab function or
as a fortran or a C routine linked to scilab.
- case 1:
when
dfunis a scilab function, its calling sequence must be:y=dfun(x [, optional parameters])(notes that even ifdfunneeds optional parameters it must appear simply asdfunin the calling sequence ofleastsq).- case 2:
when
dfunis defined by a Fortran or C routine it must appear asdfun_name(a string) in the calling sequence ofleastsq(dfun_namebeing the name of the routine which must be linked to Scilab). The calling sequences for this routine are nearly the same than forfun:In Fortran: subroutine dfun(m, n, x, params, y) integer m,n double precision x(n), params(*), y(m,n) In C: void fun(int *m, int *n, double *x, double *params, double *y)
in the C case dfun(i,j)=dfi/dxj must be stored in
y[m*(j-1)+i-1].
Remarks
Like datafit,
leastsq is a front end onto the optim function. If you want to try the
Levenberg-Marquard method instead, use lsqrsolve.
A least squares problem may be solved directly with the optim function ; in this case the function NDcost may be useful to compute the derivatives (see the NDcost help page which provides a simple example for parameters identification of a differential equation).
Examples
// We will show different calling possibilities of leastsq on one (trivial) example // which is non linear but does not really need to be solved with leastsq (applying // log linearizes the model and the problem may be solved with linear algebra). // In this example we look for the 2 parameters x(1) and x(2) of a simple // exponential decay model (x(1) being the unknow initial value and x(2) the // decay constant): function y=yth(t, x) y = x(1)*exp(-x(2)*t) endfunction // we have the m measures (ti, yi): m = 10; tm = [0.25, 0.5, 0.75, 1.0, 1.25, 1.5, 1.75, 2.0, 2.25, 2.5]'; ym = [0.79, 0.59, 0.47, 0.36, 0.29, 0.23, 0.17, 0.15, 0.12, 0.08]'; wm = ones(m,1); // measure weights (here all equal to 1...) // and we want to find the parameters x such that the model fits the given // datas in the least square sense: // // minimize f(x) = sum_i wm(i)^2 ( yth(tm(i),x) - ym(i) )^2 // initial parameters guess x0 = [1.5 ; 0.8]; // in the first examples, we define the function fun and dfun // in scilab language function e=myfun(x, tm, ym, wm) e = wm.*( yth(tm, x) - ym ) endfunction function g=mydfun(x, tm, ym, wm) v = wm.*exp(-x(2)*tm) g = [v , -x(1)*tm.*v] endfunction // now we could call leastsq: // 1- the simplest call [f,xopt, gropt] = leastsq(list(myfun,tm,ym,wm),x0) // 2- we provide the Jacobian [f,xopt, gropt] = leastsq(list(myfun,tm,ym,wm),mydfun,x0) // a small graphic (before showing other calling features) tt = linspace(0,1.1*max(tm),100)'; yy = yth(tt, xopt); clf() plot2d(tm, ym, style=-2) plot2d(tt, yy, style = 2) legend(["measure points", "fitted curve"]); xtitle("a simple fit with leastsq") // 3- how to get some information (we use imp=1) [f,xopt, gropt] = leastsq(1,list(myfun,tm,ym,wm),mydfun,x0) // 4- using the conjugate gradient (instead of quasi Newton) [f,xopt, gropt] = leastsq(1,list(myfun,tm,ym,wm),mydfun,x0,"gc") // 5- how to provide bound constraints (not useful here !) xinf = [-%inf,-%inf]; xsup = [%inf, %inf]; [f,xopt, gropt] = leastsq(list(myfun,tm,ym,wm),"b",xinf,xsup,x0) // without Jacobian [f,xopt, gropt] = leastsq(list(myfun,tm,ym,wm),mydfun,"b",xinf,xsup,x0) // with Jacobian // 6- playing with some stopping parameters of the algorithm // (allows only 40 function calls, 8 iterations and set epsg=0.01, epsf=0.1) [f,xopt, gropt] = leastsq(1,list(myfun,tm,ym,wm),mydfun,x0,"ar",40,8,0.01,0.1) // 7 and 8: now we want to define fun and dfun in fortran then in C // Note that the "compile and link to scilab" method used here // is believed to be OS independant (but there are some requirements, // in particular you need a C and a fortran compiler, and they must // be compatible with the ones used to build your scilab binary). // 7- fun and dfun in fortran // 7-1/ Let 's Scilab write the fortran code (in the TMPDIR directory): f_code = [" subroutine myfun(m,n,x,param,f)" "* param(i) = tm(i), param(m+i) = ym(i), param(2m+i) = wm(i)" " implicit none" " integer n,m" " double precision x(n), param(*), f(m)" " integer i" " do i = 1,m" " f(i) = param(2*m+i)*( x(1)*exp(-x(2)*param(i)) - param(m+i) )" " enddo" " end ! subroutine fun" "" " subroutine mydfun(m,n,x,param,df)" "* param(i) = tm(i), param(m+i) = ym(i), param(2m+i) = wm(i)" " implicit none" " integer n,m" " double precision x(n), param(*), df(m,n)" " integer i" " do i = 1,m" " df(i,1) = param(2*m+i)*exp(-x(2)*param(i))" " df(i,2) = -x(1)*param(i)*df(i,1)" " enddo" " end ! subroutine dfun"]; cd TMPDIR; mputl(f_code,TMPDIR+'/myfun.f') // 7-2/ compiles it. You need a fortran compiler ! names = ["myfun" "mydfun"] flibname = ilib_for_link(names,"myfun.f",[],"f"); // 7-3/ link it to scilab (see link help page) link(flibname,names,"f") // 7-4/ ready for the leastsq call: be carreful do not forget to // give the dimension m after the routine name ! [f,xopt, gropt] = leastsq(list("myfun",m,tm,ym,wm),x0) // without Jacobian [f,xopt, gropt] = leastsq(list("myfun",m,tm,ym,wm),"mydfun",x0) // with Jacobian // 8- last example: fun and dfun in C // 8-1/ Let 's Scilab write the C code (in the TMPDIR directory): c_code = ["#include <math.h>" "void myfunc(int *m,int *n, double *x, double *param, double *f)" "{" " /* param[i] = tm[i], param[m+i] = ym[i], param[2m+i] = wm[i] */" " int i;" " for ( i = 0 ; i < *m ; i++ )" " f[i] = param[2*(*m)+i]*( x[0]*exp(-x[1]*param[i]) - param[(*m)+i] );" " return;" "}" "" "void mydfunc(int *m,int *n, double *x, double *param, double *df)" "{" " /* param[i] = tm[i], param[m+i] = ym[i], param[2m+i] = wm[i] */" " int i;" " for ( i = 0 ; i < *m ; i++ )" " {" " df[i] = param[2*(*m)+i]*exp(-x[1]*param[i]);" " df[i+(*m)] = -x[0]*param[i]*df[i];" " }" " return;" "}"]; mputl(c_code,TMPDIR+'/myfunc.c') // 8-2/ compiles it. You need a C compiler ! names = ["myfunc" "mydfunc"] clibname = ilib_for_link(names,"myfunc.c",[],"c"); // 8-3/ link it to scilab (see link help page) link(clibname,names,"c") // 8-4/ ready for the leastsq call [f,xopt, gropt] = leastsq(list("myfunc",m,tm,ym,wm),"mydfunc",x0)
| << karmarkar | Optimization and Simulation | lsqrsolve >> |