Аргументы

zu

вектор-столбец длиной M. Решение ОДУ, вычисленное по сетке, заданной точками. Она содержит z(u(x)) для каждой искомой точки;

xpoints

массив, который содержит точки для которых нужно найти решение;

N

скаляр с целочисленным значением, количество дифференциальных уравнений (N <= 20).

m

вектор размером N с целочисленными элементами. Это вектор порядка каждого из дифференциальных уравнений: m(i) указывает порядок i-го дифференциального уравнения. Далее, M будет представлять сумму элементов m.

x_low

скаляр: левый конец интервала

x_up

скаляр: правый конец интервала

zeta

вектор размером M; zeta(j) указывает j-тую точку граничного условия (граничную точку). Необходимо, чтобы выполнялось условие x_low<=zeta(j)<=zeta(j+1)<=x_up.

Все точки граничных условий должны составлять сетку точек во всех используемых сетках, см. ниже описание ipar(11) и fixpnt.

ipar

массив с 11-ю целочисленными элементами:

[nonlin, collpnt, subint, ntol, ndimf, ndimi, iprint, iread, iguess, rstart,nfxpnt]

nonlin: ipar(1)

0, если задача линейна; 1, если задача нелинейна.

collpnt: ipar(2)

Задаёт количество рядом расположенных точек на подынтервале, где max(m(j)) <= collpnt <= 7.

Если ipar(2)=0, то collpnt установлен равным max( max(m(j))+1, 5-max(m(j))).

subint: ipar(3)

Задаёт количество подынтервалов в исходной сетке. Если ipar(3) = 0, то bvode произвольным образом устанавливается subint = 5.

ntol: ipar(4)

Задаёт количество решений и допустимые отклонения производных. Требуется, чтобы 0 < ntol <= M. ipar(4) должно быть установлено равным размеру аргумента tol или равным 0. В последнем случае фактическое значение будет автоматически установлено равным size(tol,'*').

ndimf: ipar(5)

Задаёт размер fspace (вещественнозначный рабочий массив). Его значение указывает ограничение по максимальному количеству подынтервалов nmax.

Значение ipar(5) должно соответствовать ограничению ipar(5)>=nmax*nsizef, где nsizef=4 + 3*M + (5+collpnt*N)*(collpnt*N+M) + (2*M- nrec)*2*M (nrec - количество граничных условий с правой стороны).

ndimi: ipar(6)

Задаёт размер ispace (целочисленный рабочий массив). Это значение указывает ограничение по nmax, максимальному количеству подынтервалов.

Значение ipar(6) должно соответствовать ограничению ipar(6)>=nmax*nsizei, где nsizei= 3 + collpnt*N + M.

iprint: ipar(7)

контроль на выходе, может принимать следующие значения:

-1

для полной диагностической распечатки

0

для избранной распечатки

1

для отказа от распечатки

iread: ipar(8)

= 0

заставляет bvode генерировать равномерную исходную сетку.

= xx

другие значения в Scilab'е пока не реализованы

= 1

если исходная сетка указана пользователем, то она будет определена в fspace следующим образом: сетка будет занимать fspace(1), ..., fspace(n+1). Пользователю нужно предоставить только внутренние точки сетки fspace(j) = x(j), j = 2, ..., n.

= 2

если исходная сетка представлена пользователем как в случае ipar(8)=1, и, к тому же, никакого выбора адаптивной сетки не делается.

iguess: ipar(9)

= 0

если никакого первоначального предположения для решения не предоставлено.

= 1

если первоначальное предположение предоставлено пользователем с помощью аргумента guess.

= 2

если исходная сетка и коэффициенты приближённого решения предоставлены пользователем в fspace (прежняя и новая сетки одни и те же).

= 3

если прежняя сетка и коэффициенты приближённого решения предоставлены пользователем в fspace, а новая сетка взята в два раза реже, то есть каждая вторая точка из прежней сетки.

= 4

если в дополнение к прежней исходной сетке и коэффициента приближённого решения также предоставлена новая сетка в fspace (см. описание выходных данных для более подробной информации по iguess = 2, 3 и 4).

ireg: ipar(10)

= 0

если задача является регулярной

= 1

если первый коэффициент релаксации равен ireg, и нелинейная итерация не зависит от прошлой сходимости (использовать только для сверхчувствительных нелинейных задач) only).

= 2

если вы хотите возврата немедленно при (а) двух, следующих друг за другом, несходимостях, либо (б) после получения ошибочной оценки в первый раз.

nfxpnt: ipar(11)

указывает количество фиксированных точек в сетке, отличных от x_low и x_up (размерность fixpnt). ipar(11) должна быть установлена равной размерности аргумента fixpnt или равной 0. В последнем случае фактическое значение будет автоматически установлено равным size(fixpnt,'*').

ltol

массив размерности ntol=ipar(4). ltol(j) = l определяет, что j-тый допуск в массиве tol управляет ошибкой в l-том элементе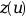 . Также требуется, чтобы:

1 <= ltol(1) < ltol(2) < ... < ltol(ntol) <= M

tol

массив размерности ntol=ipar(4).

tol(j) допуск ошибки в ltol(j)-том элементе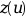 . Таким образом код пытается удовлетворить 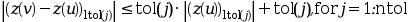в каждом подынтервале, где

- вектор приближённого решения, а 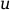- точное решение (неизвестное).

fixpnt

массив размером nfxpnt=ipar(11). Он содержит точки отличные от x_low и x_up, которые нужно включить во все сетки. Код требует, чтобы все точки дополнительных условий, отличные от x_low и x_up (см. описание zeta ) были включены в качестве фиксированных точек в fixpnt.

fsub

Внешняя функция, используемая для вычисления вектор-столбца f=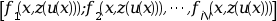 , для всех x таких, что x_low <= x <= x_up и для любых z=z(u(x)) (см. описание ниже).

Внешняя функция должна иметь заголовки:

• В Fortran последовательность вызова должна быть:

  subroutine fsub(x,zu,f)
  double precision zu(*), f(*),x
  

• В C прототип функции должен быть:

  void fsub(double *x, double *zu, double *f)
  

• А в Scilab'е:

  function f = fsub(x,zu,parameters)
  

dfsub

Внешняя функция, используемая для вычисления якобиана от f(x,z(u)) в точке x, где z(u(x)) определена как для fsub, и массив df размером N на M должен быть заполнен частными производными от f: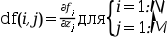

Внешняя функция должна иметь заголовки:

• В Fortran вызывающая последовательность должна быть:

  subroutine dfsub(x,zu,df)
  double precision zu(*), df(*),x
  

• В C прототип функции должен быть:

  void dfsub(double *x, double *zu, double *df)
  

• И в Scilab'е:

  function df = dfsub(x,zu,parameters)
  

gsub

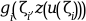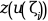
Внешняя функция, используемая для вычисления задавая z= z = zeta(i) для 1<=i<=M.

Внешняя функция должна иметь заголовки:

• В Fortran вызывающая последовательность должна быть:

  subroutine gsub(i,zu,g)
  double precision zu(*), g(*)
  integer i
  

• В C прототип функции должен быть:

  void gsub(int *i, double *zu, double *g)
  

• А в Scilab'е:

  function g = gsub(i,zu,parameters)
  

  Заметьте, что в отличие от f в fsub, здесь только одно значение за вызов возвращается в g.

dgsub

Внешняя функция, используемая для вычисления i-той строки якобиана от g(x,u(x)), где z(u) такая, как для fsub, i как для gsub а M-вектор dg должен быть заполнен частными производными от g, то есть, для отдельного вызова вычисляется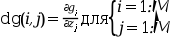

Внешняя функция должна иметь заголовки:

• В Fortran вызывающая последовательность должна быть:

  subroutine dgsub(i,zu,dg)
  double precision zu(*), dg(*)
  

• В C прототип функции должен быть:

  void dgsub(int *i, double *zu, double *dg)
  

• А в Scilab'е:

  function dg = dgsub(i,zu,parameters)
  

guess

Внешняя функция, используемая для вычисления исходной аппроксимации для z(u(x)) и dmval(u(x)), вектора mj-тых производных от u(x). Заметьте, что эта процедура используется только если ipar(9) = 1, и тогда все M элементы zu и N элементы dmval должны быть вычислены для любого x такого, что x_low <= x <= x_up.

Внешняя функция должна иметь заголовки:

• В Fortran вызывающая последовательность должна быть:

  subroutine guess(x,zu,dmval)
  double precision x,z(*), dmval(*)
  

• В C прототип функции должне быть:

  void fsub(double *x, double *zu, double *dmval)
  

• А в Scilab'е:

  function [dmval,zu] = fsub(x,parameters)
  

<optional_args>

Необязательные аргументы, должны быть либо:

• любой левой частью упорядоченной последовательности значений: guess, dfsub, dgsub, fixpnt, ndimf, ndimi, ltol, tol, ntol,nonlin, collpnt, subint, iprint, ireg, ifail

• либо любой последовательностью arg_name=argvalue с arg_name из: guess, dfsub, dgsub, fixpnt, ndimf, ndimi, ltol, tol, ntol, nonlin, collpnt, subint, iprint, ireg, ifail.

Все эти аргументы за исключением ifail описаны выше. ifail может использоваться для отображения вызова bvode в соответствии с выбранными необязательными аргументами. Если guess задано, то iguess равно 1.

Описание

Эти функции решают задачу многоточечных граничных значений для системы ОДУ смешанного порядка, заданной как:

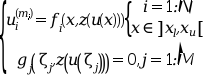
где:

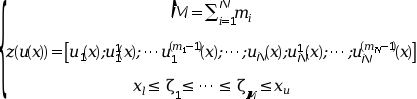
Аргумент zu, используемый внешними функциями и возвращаемый bvode, является вектор-столбцом, сформированным элементами z(u(x)) для заданных x.

Метод, используемый для аппроксимации решения, u является коллокацией в гауссовских точках, требующих m(i)-1 непрерывных производных в i-том элементе, i = 1:N. Здесь, k - количество точек коллокации (этапов) на подынтервале, и оно выбирается так, чтобы k ≥ max(m(i)). Используется представление решения одночленного решения Рунге-Кутты.

Примеры

Первые две задачи взяты из [1] раздела Литература.

• Задача 1 описывает однородно нагруженную балку переменной жёсткости просто поддерживаемую на обоих концах.

  Она может быть определена следующим образом.

  Решим дифференциальное уравнение четвёртого порядка:

  

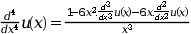
  Налагаемые граничные условия:

  

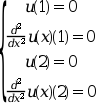
  Известно точное решение этой задачи:

  

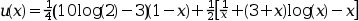
  N = 1; // только одно дифференциальное уравнение
  m = 4; // дифференциальное уравнение четвёртого порядка
  M = sum(m);
  
  x_low = 1;
  x_up = 2; // пределы x
  zeta = [x_low,x_low,x_up,x_up]; // два ограничения (на значение u и его вторую производную) на каждой границе.
  
  // Внешние функции
  // Эти функции вызываются программой решения с zu=[u(x);u'(x);u''(x);u'''(x)]
  
  // - Функция, которая вычисляет правую сторону дифференциального уравнения
  function f=fsub(x, zu)
      f = (1 - 6*x^2*zu(4) - 6*x*zu(3)) / x^3
  endfunction
  
  // - Функция, которая вычисляет производную fsub по zu
  function df=dfsub(x, zu)
      df = [0,0,-6/x^2,-6/x]
  endfunction
  
  // - Функция, которая вычисляет i-тое ограничение для заданной i
  function g=gsub(i, zu),
    select i
    case 1 then  // x = zeta(1) = 1
      g = zu(1)  // u(1)=0
    case 2 then  // x = zeta(2) = 1
      g = zu(3)  // u''(1) = 0
    case 3 then  // x = zeta(3) = 2
      g = zu(1)  // u(2) = 0
    case 4 then  // x = zeta(4) = 2
      g = zu(3)  // u''(2) = 0
    end
  endfunction
  
  // - Функция, которая вычисляет производную gsub по z
  function dg=dgsub(i, z)
    select i
    case 1 then   // x = zeta(1) = 1
      dg = [1,0,0,0]
    case 2 then   // x = zeta(2) = 1
      dg = [0,0,1,0]
    case 3 then   // x = zeta(3) = 2
      dg = [1,0,0,0]
    case 4 then   // x = zeta(4) = 2
      dg = [0,0,1,0]
    end
  endfunction
  
  // - Функция, которая вычисляет начальное предположение, здесь не используемое
  function [zu, mpar]=guess(x)
      zu = 0;
      mpar = 0;
  endfunction
  
   // определим функцию, которая вычисляет точное значение u для заданного x (в целях проверки)
  function zu=trusol(x)
    zu = 0*ones(4,1)
    zu(1) =  0.25*(10*log(2)-3)*(1-x) + 0.5 *( 1/x   + (3+x)*log(x) - x)
    zu(2) = -0.25*(10*log(2)-3)       + 0.5 *(-1/x^2 + (3+x)/x      + log(x) - 1)
    zu(3) = 0.5*( 2/x^3 + 1/x   - 3/x^2)
    zu(4) = 0.5*(-6/x^4 - 1/x/x + 6/x^3)
  endfunction
  
  fixpnt = []; // Все граничные условия находятся в x_low и x_up
  
  //    nonlin  collpnt n ntol ndimf  ndimi iprint iread iguess rstart nfxpnt
  ipar = [0       0     1  2   2000    200    1      0     0      0      0   ]
  
  ltol = [1,3]; // установка контроля допуска на zu(1) и zu(3)
  tol = [1.e-11,1.e-11]; // установка значений допуска для контроля допуска
  xpoints = x_low:0.01:x_up;
  
  zu = bvode(xpoints, N, m, x_low,x_up, zeta, ipar, ltol,tol, fixpnt,...
            fsub, dfsub, gsub, dgsub, guess)
  //проверка ограничений
  zu([1,3],[1 $]) // должно быть нулевым
  plot(xpoints, zu(1,:)) // процесс решения u
  zu1 = [];
  for x = xpoints
      zu1 = [zu1,trusol(x)];
  end
  norm(zu-zu1)

• Та же задача с использованием bvodeS и начальным предположением.

  function [z, lhS]=zstart(x)
    z = zeros(5,1); z(5) = 1;
    lhS = [0;1];
  endfunction
  zu = bvode(xpoints, N, m, x_low, x_up, zeta, ltol=ltol, tol=tol, guess=zstart)

• Задача 2 описывает малую конечную деформацию тонкой мелкой сферической чаши постоянной толщины, подверженной квадратично меняющемуся асимметричному распределению внешнего давления. Здесь φ описывает изменение угла по меридиану деформированной стенки, а ψ является функцией напряжений. Для ε = μ = 10^-3 можно найти два различных решения в зависимости от точки начала.

  

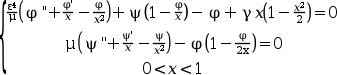
  Граничные условия:

  

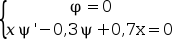
  для x=0 и x=1

  N = 2; // два дифференциальных уравнения
  m = [2 2]; // каждое дифференциальное уравнение второго порядка
  M = sum(m);
  
  x_low = 0; x_up = 1; // пределы по x
  zeta = [x_low,x_low, x_up x_up]; // два ограничения на каждой границе
  
  // Внешние функции
  // Эти функции вызываются программой решения с zu = [u1(x) ; u1'(x) ; u2(x) ; u2'(x)]
  
  // - Функция, которая вычисляет правую сторону дифференциального уравнения
  function f=fsub2(x, zu, eps, dmu, eps4mu, gam, xt),
     f = [zu(1)/x^2-zu(2)/x+(zu(1)-zu(3)*(1-zu(1)/x)-gam*x*(1-x^2/2))/eps4mu //phi''
          zu(3)/x^2-zu(4)/x+zu(1)*(1-zu(1)/(2*x))/dmu];//psi''
  endfunction
  
  // - Функция, которая вычисляет производную от fsub по zu
  function df=dfsub2(x, zu, eps, dmu, eps4mu, gam, xt),
    df = [1/x^2+(1+zu(3)/x)/eps4mu, -1/x, -(1-zu(1)/x)/eps4mu, 0
         (1-zu(1)/x)/dmu             0    1/x^2              -1/x];
  endfunction
  
  // - Функция, которая вычисляет i-тое ограничение для заданного i
  function g=gsub2(i, zu),
    select i
    case 1 then  // x = zeta(1) = 0
      g = zu(1)  // u(0) = 0
    case 2 then  // x = zeta(2) = 0
      g = -0.3*zu(3) // x*psi'-0.3*psi+0.7x = 0
    case 3 then  // x = zeta(3) = 1
      g = zu(1)  // u(1) = 0
    case 4 then  //x=zeta(4)=1
      g = 1*zu(4) - 0.3*zu(3) + 0.7*1 // x*psi'-0.3*psi+0.7x = 0
    end
  endfunction
  
  // - Функция, которая вычисляет производную от gsub по z
  function dg=dgsub2(i, z)
    select i
    case 1 then   // x = zeta(1) = 1
      dg = [1,0,0,0]
    case 2 then   // x = zeta(2) = 1
      dg = [0,0,-0.3,0]
    case 3 then   // x = zeta(3) = 2
       dg = [1,0,0,0]
    case 4 then   // x = zeta(4) = 2
      dg = [0,0,-0.3,1]
    end
  endfunction
  
  gam = 1.1
  eps = 1d-3
  dmu = eps
  eps4mu = eps^4/dmu
  xt = sqrt(2*(gam-1)/gam)
  
  fixpnt = []; // все граничные условия размещены в x_low и x_up
  collpnt = 4;
  nsizef = 4 + 3*M + (5+collpnt*N)*(collpnt*N+M)+(2*M-2)*2*M ;
  nsizei = 3 + collpnt*N+M;
  nmax = 200;
  //    nonlin  collpnt n  ntol ndimf        ndimi        iprint iread iguess rstart nfxpnt
  ipar = [1     collpnt 10  4   nmax*nsizef  nmax*nsizei   -1      0     0      0      0   ];
  
  ltol = 1:4; // установка контроля допусков на zu(1), zu(2), zu(3) и zu(4)
  tol = [1.e-5,1.e-5,1.e-5,1.e-5]; // установка значений допусков для этих четырёх значений контроля
  xpoints = x_low:0.01:x_up;
  
  // - Функция, которая вычисляет начальное предположение, здесь не используемое
  function [zu, dmval]=guess2(x, gam),
     cons = gam*x*(1-x^2/2)
     dcons = gam*(1-3*x^2/2)
     d2cons = -3*gam*x
     dmval = zeros(2,1)
     if x>xt then
       zu = [0 0 -cons -dcons]
       dmval(2) = -d2cons
     else
       zu = [2*x;2;-2*x+cons;-2*dcons]
       dmval(2) = d2cons
     end
  endfunction
  
  zu = bvode(xpoints, N, m, x_low, x_up, zeta, ipar, ltol, tol, fixpnt,...
             fsub2, dfsub2, gsub2, dgsub2, guess2);
  scf(1); clf(); plot(xpoints, zu([1 3],:)) // процесс решения phi и psi
  
  //использование начального предположения
  ipar(9) = 1; // iguess
  
  zu2 = bvode(xpoints, N, m, x_low, x_up, zeta, ipar, ltol, tol, fixpnt,...
              fsub2, dfsub2, gsub2, dgsub2, guess2);
  scf(2); clf(); plot(xpoints, zu2([1 3],:)) // процесс решения phi и psi

• Задача нахождения собственных значений

  // y''(x) = -la*y(x)
  // BV: y(0)=y'(0); y(1)=0
  // Собственные функции и собственные значения y(x,n)=sin(s(n)*(1-x)), la(n)=s(n)^2,
  // где s(n) - нули f(s,n)=s+atan(s)-(n+1)*pi, n=0,1,2,...
  // Чтобы получить третье граничное условие, мы выбираем y(0)=1
  // (с y(x) также c*y(x) является решением для каждой константы c.)
  // Решим следующую систему ОДУ:
  // y'' = -la*y
  // la' = 0
  // BV: y(0)=y'(0), y(0)=1; y(1)=0
  // z = [y(x) ; y'(x) ; la]
  
  function rhs=fsub(x, z)
    rhs = [-z(3)*z(1) ; 0]
  endfunction
  
  function g=gsub(i, z)
    g = [z(1)-z(2), z(1)-1, z(1)]
    g = g(i)
  endfunction
  
  // Следующая начальная функция годится для первых 8 собственных функций.
  function [z, lhs]=ystart(x, z, la0)
    z = [1 ; 0 ; la0]
    lhs = [0 ; 0]
  endfunction
  
  a = 0; b = 1;
  m = [2;1];
  n = 2;
  zeta = [a a b];
  N = 101;
  x = linspace(a,b,N)';
  
  // Имеем s(n)-(n+1/2)*pi -> 0 для n, стремящемся к бесконечности.
  la0 = evstr(x_dialog('n-ное собственное значение: n= ?','10'));
  la0 = (%pi/2+la0*%pi)^2;
  
  z = bvodeS(x, m, n, a, b, fsub, gsub, zeta, ystart=list(ystart,la0));
  // Тот же вызов без вывода на экран
  z = bvodeS(x, m, n, a, b, fsub, gsub, zeta, ystart=list(ystart,la0), iprint=1);
  // Тот же вызов с подробным выводом на экран
  z = bvodeS(x, m, n, a, b, fsub, gsub, zeta, ystart=list(ystart,la0), iprint=-1);
  
  clf()
  plot(x, [z(1,:)' z(2,:)'])
  xtitle(['Начальное значение =  '+string(la0);'Собственное значение = '+string(z(3,1))],'x',' ')
  legend(['y(x)';'y''(x)']);

  

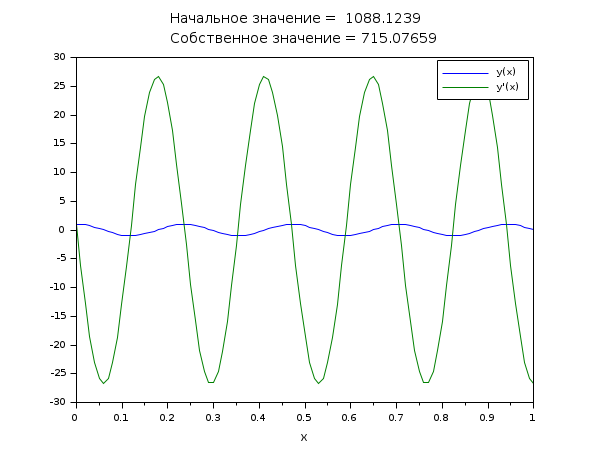
• Краевая задача, у которой решений больше одного

  // DE: y''(x)=-exp(y(x))
  // BV: y(0)=0; y(1)=0
  // Эта краевая задача имеет более одного решения.
  // Показано как найти два из них с помощью некоторой
  // предварительной информации о решениях y(x) для построения функции ystart.
  // z=[y(x);y'(x)]
  
  [a, b, m, n] = (0, 1, 2, 1);
  zeta = [a b];
  N = 101;
  tol = 1e-8*[1 1];
  x = linspace(a,b,N);
  
  function rhs=fsub(x, z), rhs=-exp(z(1)); endfunction
  
  function g=gsub(i, z)
    g = [z(1) z(1)]
    g = g(i)
  endfunction
  
  function [z, lhs]=ystart(x, z, M)
    //z = [4*x*(1-x)*M ; 4*(1-2*x)*M]
    z = [M;0]
    //lhs = [-exp(4*x*(1-x)*M)]
    lhs = 0
  endfunction
  
  for M = [1 4]
     if M==1
        z = bvodeS(x, m, n, a, b, fsub, gsub, zeta, ystart=list(ystart,M), tol=tol);
     else
        z1 = bvodeS(x, m, n, a, b, fsub, gsub, zeta, ystart=list(ystart,M), tol=tol);
     end
  end
  
  // Интегрирование ОДУ даёт, например, два решения yex и yex1.
  
  function y=f(c)
      y = c.*(1-tanh(sqrt(c)/4).^2) - 2;
  endfunction
  c = fsolve(2,f);
  
  function y=yex(x, c)
    y = log(c/2*(1-tanh(sqrt(c)*(1/4-x/2)).^2))
  endfunction
  
  function y=f1(c1)
      y = 2*c1^2+tanh(1/4/c1)^2 - 1;
  endfunction
  c1 = fsolve(0.1, f1);
  
  function y=yex1(x, c1)
    y = log((1-tanh((2*x-1)/4/c1).^2)/2/c1/c1)
  endfunction
  
  disp('norm(yex(x)-z(1,:))= ', norm(z(1,:)-yex(x)))
  disp('norm(yex1(x)-z1(1,:))= ', norm(z1(1,:)-yex1(x)))
  clf
  subplot(2,1,1)
  plot2d(x, z(1,:), style=5)
  xtitle('Два различных решения','x',' ')
  subplot(2,1,2)
  plot2d(x, z1(1,:), style=5)
  xtitle(' ','x',' ')

  

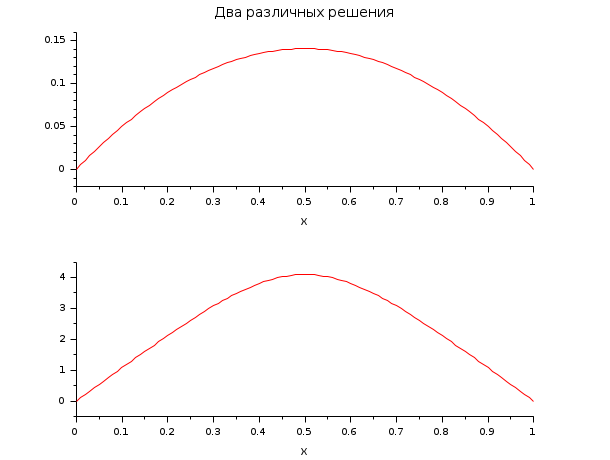
• Многоточечная краевая задача

  // DE y'''(x)=1
  // z=[y(x);y'(x);y''(x)]
  // BV: y(-1)=2 y(1)=2
  // Дополнительное условие: y(0)=1
  
  [a, b, c] = (-1, 1, 0);
  // Точка дополнительного условия c должна быть включена в массив fixpnt.
  [m, n] = (3, 1);
  
  function rhs=fsub(x, z)
    rhs = 1
  endfunction
  
  function g=gsub(i, z)
    g = [z(1)-2 z(1)-1 z(1)-2]
    g = g(i)
  endfunction
  
  N = 10;
  zeta = [a c b];
  x = linspace(a,b,N);
  
  z = bvodeS(x, m, n, a, b, fsub, gsub, zeta, fixpnt=c);
  
  function y=yex(x)
      y = x.^3/6 + x.^2 - x./6 + 1
  endfunction
  
  disp(norm(yex(x)-z(1,:)),'norm(yex(x)-z(1,:))= ')

• Квантовое уравнение Неймана с 2 "собственными значениями" (c_1 и c2). Используется продолжение.

  // Квантовое уравнение Неймана с 2 "собственными значениями" c_1 и c_2
  // (c_1=v-c_2-c_3, где v - параметр, используемый в продолжении)
  //
  // diff(f,x,2) + (1/2)*(1/x + 1/(x-1) + 1/(x-y))*diff(f,x)
  //      - (c_1/x + c_2/(x-1) + c_3/(x-y))* f(x) = 0
  // diff(c_2,x)=0,  diff(c_3,x) = 0
  //
  // и 4 "граничных" условия: diff(f,x)(a_k)=2*c_k*f(a_k) для
  // k=1,2,3, a_k=(0, 1 , y)  и нормировка f(1) = 1
  //
  // Вектор z - это z_1=f, z_2=diff(f,x), z_3=c_2 и z_4=c_3
  // Предположение выбирается так, чтобы иметь один узел в интервале
  // [0,1],  f(x)=2*x-1 такая, что f(1)=1, c_2 и c_3 выбираются так,
  // чтобы исключить полюсы в дифференциальном уравнении в 1.0 и
  // y, z_3=1, z_4=1/(2*y-1)
  // См.: http://arxiv.org/pdf/hep-th/0407005
  
  y = 1.9d0;
  eigens = zeros(3,40); // Для хранения результатов
  
  // Общая настройка bvode
  
  // Количество дифференциальных уравнений
  ncomp = 3;
  
  // Порядки уравнений
  m = [2, 1, 1];
  
  // Нелинейная задача
  ipar(1) = 1;
  
  // Количество точек коллокации
  ipar(2) = 3;
  
  // Исходная сетка из 4 подынтервалов
  ipar(3) = 4;
  ipar(8) = 0;
  
  // Размер fspace, ispace, см. colnew.f для изменения размера
  ipar(5) = 30000;
  ipar(6) = 2000;
  
  // Средний вывод данных
  ipar(7) = 0;
  
  // Есть исходное приближение
  ipar(9) = 1;
  
  // fixpnt - это массив, содержащий все фиксированные точки в сетке, в
  // частности, "граничные" точки, за исключением aleft и aright, ipar[11]
  // её размер, здесь только одна внутренняя "граничная точка"
  ipar(11) = 1;
  fixpnt = [1.0d0];
  
  // Допустимые отклонения для всех элементов z_1, z_2, z_3, z_4
  ipar(4) = 4;
  
  // Проверка допустимого отклонения для f и diff(f,x) и для c_2 и c_3
  ltol = [1, 2, 3, 4];
  tol = [1d-5, 1d-5, 1d-5, 1d-5];
  
  // Определение дифференциальных уравнений
  
  function f=fsub(x, z)
      f = [ -.5*(1/x+1/(x-1)+1/(x-y))*z(2) +...
           z(1) * ((v-z(3)-z(4))/x + z(3)/(x-1) + z(4)/(x-y)), 0, 0];
  endfunction
  function df=dfsub(x, z)
      df = [(v-z(3)-z(4))/x + z(3)/(x-1) + z(4)/(x-y),...
      -.5*(1/x+1/(x-1)+1/(x-y)),z(1)/(x*(x-1)),z(1)*y/(x*(x-y));...
      0,0,0,0;0,0,0,0];
  endfunction
  
  // Граничные условия
  
  function g=gsub(i, z)
      select i
      case 1, g = z(2) - 2*z(1)*(v-z(3)-z(4))
      case 2, g = z(2) - 2*z(1)*z(3)
      case 3, g = z(1)-1.
      case 4, g = z(2) - 2*z(1)*z(4)
      end
  endfunction
  function dg=dgsub(i, z)
          select i
          case 1, dg = [-2*(v-z(3)-z(4)),1.,2*z(1),2*z(1)]
          case 2, dg = [-2*z(3),1.,-2*z(1),0]
          case 3, dg = [1,0,0,0]
          case 4, dg = [-2*z(4),1.,0,-2*z(1)]
          end
  endfunction
  
  // Начало вычисления
  
  // Положения краевых условий, отсортированные
  zeta = [0.0d0, 1.0d0, 1.0d0, y];
  // Края интервала
  aleft = 0.0d0;
  aright = y;
  
  // Массив из 40 значений v, исследуемых продолжением, и массив из 202
  // точек, в которых следует вычислить функцию f.
  valv = [linspace(0,.9,10) logspace(0,2,30)];
  res = [linspace(0,.99,100) linspace(1,y,101)];
  
  // Собственные состояния характеризуются количеством узлов на интервале
  // [0,1] и на [1,y], здесь предполжение выбирает один узел (ноль) на
  // интервале [0,1] с линейной функцией f(x)=2*x-1 и константами c_2, c_3,
  // так что dmval=0. Заметьте, что вектор z имеет mstar = 4 элементов,
  // в то время как dmval имеет ncomp = 3 элемента.
  
  function [z, dmval]=guess(x)
       z = [2*x-1, 2., 1., 1/(2*y-1)]
       dmval = [0,0,0]
  endfunction
  
  // Первое выполнение имеет ipar(9)=1 и использует предположение
  // Последующие выполнения имеют ipar(9)=3 и используют продолжение.
  // Это выполняется в плотно закрытом цикле, чтобы не нарушить стек
  
  for i = 1:40
      v = valv(i);
      sol = bvode(res, ncomp, m, aleft, aright, zeta, ipar, ltol, tol, fixpnt,...
                  fsub, dfsub, gsub, dgsub, guess);
      eigens(:,i) = [v;sol(3,101);sol(4,101)];  // c_2 и c_3 являются константами!
      ipar(9) = 3;
  end
  
  // Чтобы увидеть изменение собственных значений с v, disp(eigens)
  // Обратите внимание на то, что они изменяются гладко.
  // Чтобы увидеть решение f для v=40, disp(sol(1,:)).
  // Обратите внимание на то, что оно исчезает точно один раз в
  // [0,1] в x близком  0.98, и становится очень малым, когда
  // x -> 0 и очень большим, когда x -> y.
  // Это явно отличается от случая при малом v.
  // Процедура продолжения позволяет исследовать эти экспоненциальные
  // поведения без перехода в другие собственные состояния.

Используемые функции

Эта функция основана на процедуре Fortran colnew, разработанной

U. Ascher, Department of Computer Science, University of British Columbia, Vancouver, B.C. V6T 1W5, Canada

G. Bader, institut f. Angewandte mathematik university of Heidelberg; im Neuenheimer feld 294d-6900 Heidelberg 1

Литература

1. U. Ascher, J. Christiansen and R.D. Russell, collocation software for boundary-value ODEs, acm trans. math software 7 (1981), 209-222. this paper contains EXAMPLES where use of the code is demonstrated.

2. G. Bader and U. Ascher, a new basis implementation for a mixed order boundary value ode solver, siam j. scient. stat. comput. (1987).

3. U. Ascher, J. Christiansen and R.D. Russell, a collocation solver for mixed order systems of boundary value problems, math. comp. 33 (1979), 659-679.

4. U. Ascher, J. Christiansen and R.D. russell, colsys - a collocation code for boundary value problems, lecture notes comp.sc. 76, springer verlag, b. children et. al. (eds.) (1979), 164-185.

5. C. Deboor and R. Weiss, solveblok: a package for solving almost block diagonal linear systems, acm trans. math. software 6 (1980), 80-87.

Смотрите также

• link — dynamic linker
• external — объект Scilab'а, внешняя функция или подпрограмма
• ode — программа решения обыкновенных дифференциальных уравнений
• dae — Differential algebraic equations solver