bezier
compute the points for the bezier curve
Syntax
z = bezier(p, t [,w])
Arguments
- p
a 2 or 3 columns matrix containing the control points (P0, P1, ..., Pn).
- t
a scalar or row vector.
If
tis scalar,tcontains the number of points of Bezier curves. In this case, thebezierfunction createlinspace(0, 1, t)vector. Iftis vector, this values must be in [0; 1]- w
a column vector. It contains the weight to apply on each point. This vector must have the same number of rows as p
- z
a 2 or 3 columns matrix
Description
This function computes a matrix of points on the Bezier curve
defined by the n+1 control points P.
P must be defined as: [xp0 yp0; xp1 yp1; ...; xpn ypn] to create the 2-D Bezier curve or
[xp0 yp0 zp0; xp1 yp1 zp1; ...; xpn ypn zpn]. for 3-D Bezier curve.
From [P0, P1, ..., Pn] control points, the bezier curve is the set of points defined by the parametric representation
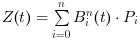 for
for ![t \in [0;1]](/docs/2024.1.0/ru_RU/_LaTeX_bezier.xml_2.png) and
and
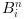 are the Bernstein polynoms.
are the Bernstein polynoms.
Examples
2d Bezier curve
P = [0 0; 1 2; 2 0; -1 0]; t = linspace(0, 1, 100); z = bezier(P, t); plot(z(:,1), z(:, 2), "b", "thickness", 3); plot(P(:,1), P(:,2), "r.", "thickness", 3); gca().data_bounds = [-2 -1; 3 3];
P = [0 0; 0 1; 1 1; 1 0]; nb = 50; z = bezier(P, nb); plot(z(:,1), z(:, 2), "b", "thickness", 3); plot(P(:,1), P(:,2), "r.", "thickness", 3); gca().data_bounds = [-0.2 -0.2; 1.2 1.2]; xgrid();
P = [0 0; 1 1; 3 0; 5 -1; 1 -1]; t = linspace(0, 1, 100); z = bezier(P, t); plot(z(:,1), z(:, 2), "b", "thickness", 3); plot(P(:,1), P(:,2), "r.", "thickness", 3); gca().data_bounds = [-2 -1; 4 2];
3d Bezier curve
P = [0 0 0; 1 2 1; 2 0 2; -1 0 1]; t = linspace(0, 1, 100); z = bezier(P, t); drawlater(); param3d(P(:,1), P(:,2), P(:, 3)); a = gca(); a.data_bounds = [-1.3 -0.3 -0.3;2.3 2.3 2.3]; e = gce(); e.mark_mode = "on"; e.mark_style = 10; e.line_mode = "off"; e.mark_foreground = color("red"); param3d(z(:,1), z(:,2), z(:,3)); e = gce(); e.foreground = color("blue"); e.thickness = 3; drawnow(); a.rotation_angles = [74.5 21.25];
See also
- bernstein — compute the n-order Bernstein matrix
History
| Версия | Описание |
| 2024.1.0 | Introduction in Scilab. |
| Report an issue | ||
| << Interpolation | Interpolation | bsplin3val >> |