grand

Paramètres

m, n, o

entiers : dimensions de la matrice de nombres aléatoires à obtenir Y

X

un vecteur, une matrice ou une hypermatrice dont seules les dimensions (m x n x ...) sont utilisées

PDFname

Nom de la fonction de densité de probabilité choisie : "def", "unf", "uin", "bet", "gam","exp", "nor", "geo", "poi", "bin", "chi", "nbn", "nch", "f", "nf", "lgi".

Y

Vecteur, matrice ou hypermatrice des nombres aléatoires générés, de taille m x n x ... (encodage décimal)

S

résultat de l'action (une chaîne ou un vecteur colonne)

Description

Cette fonction produit des nombres aléatoires selon différentes distributions de probabilité.

Les séquences d'appel

Y = grand(m, n, "bet", A, B)
Y = grand(m, n, "bin", N, p)
Y = grand(m, n, "nbn", N, p)
Y = grand(m, n, "chi", Df)
Y = grand(m, n, "nch", Df, Xnon)
Y = grand(m, n, "exp", Av)
Y = grand(m, n, "f", Dfn, Dfd)
Y = grand(m, n, "nf", Dfn, Dfd, Xnon)
Y = grand(m, n, "gam", shape, rate)
Y = grand(m, n, "nor", Av, Sd)
Y = grand(m, n, "geom", p)
Y = grand(m, n, "poi", mu)
Y = grand(m, n, "def")
Y = grand(m, n, "unf", Low, High)
Y = grand(m, n, "uin", Low, High)
Y = grand(m, n, "lgi")

La syntaxe

Y = grand(m, n, o, …, PDFname, …)

Y = grand(X, PDFname, …)

Les séquences d'appel

Y = grand(n, "mn", Mean, Cov)
Y = grand(n, "markov", P, x0)
Y = grand(n, "mul", nb, P)
Y = grand(n, "prm", array)

Les séquences d'appel

S = grand("getgen")
grand("setgen", gen)

S = grand("getsd")
grand("setsd", S)

grand("setcgn", G)
S = grand("getcgn")

grand("initgn", I)

grand("setall", s1, s2, s3, s4)

grand("advnst", K)

Générer des nombres aléatoires selon une loi donnée

beta

Y = grand(m, n, "bet", A, B) génère des nombres aléatoires suivant la loi beta de paramètres A and B. La densité de cette loi est (0 < x < 1) :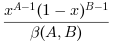

A et B devant être des réels > 10^-37. Fonction(s) associée(s) : cdfbet.

binomiale

Y = grand(m, n, "bin", N, p) génère des nombres aléatoires suivant la loi binomiale de paramètres N (entier > 0) et p (réel dans [0,1]) : nombre de succès au cours de N épreuves de Bernouilli de probabilité de succès p. Fonctions associées : binomial, cdfbin.

binomiale négative

Y = grand(m, n, "nbn", N, p) génère des nombres aléatoires suivant la loi binomiale négative de paramètres N (entier > 0) et p (réel dans ]0,1[) : nombre d'échecs avant d'obtenir N succès dans des épreuves de Bernouilli de probabilité de succès p. Fonction associée : cdfnbn.

chi 2

Y = grand(m, n, "chi", Df) génère des nombres aléatoires suivant la loi du chi 2 à Df (réel > 0.0) degrés de liberté. Fonction associée : cdfchi.

chi 2 non centrée

Y = grand(m, n, "nch", Df, Xnon) génère des nombres aléatoires suivant la loi du chi 2 non centrée à Df degrés de liberté (réel >= 1.0) le paramètre de décentrage étant Xnonc (réel >= 0.0). Fonction associée : cdfchn.

exponentielle

Y = grand(m, n, "exp", Av) génère des nombres aléatoires suivant la loi exponentielle de moyenne Av (réel >= 0.0).

F variance ratio

Y = grand(m, n, "f", Dfn, Dfd) génère des nombres aléatoires suivant la loi F (variance ratio) à Dfn (réel > 0.0) degrés de liberté au numérateur et Dfd (réel > 0.0) degrés de liberté au dénominateur. Fonction associée : cdff.

non central F variance ratio

Y = grand(m, n, "nf", Dfn, Dfd, Xnon) génère des nombres aléatoires suivant la loi F (variance ratio) non centrée à Dfn (réel >= 1) degrés de liberté au numérateur, et Dfd (réel > 0) degrés de liberté au dénominateur, Xnonc (réel >= 0) étant le paramètre de décentrage. Fonction associée : cdffnc.

gamma

Y = grand(m, n, "gam", shape, rate) génère des nombres aléatoires suivant la loi gamma de paramètres shape (réel > 0) et scale (réel > 0). La densité est :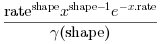

Fonctions associées : gamma, cdfgam.

Gauss Laplace (normale)

Y = grand(m, n, "nor", Av, Sd) génère des nombres aléatoires suivant la loi normale, de moyenne Av (réel) et d'écart type Sd (réel >= 0). Fonctions associées : cdfnor, erf.

multi normale

Y = grand(n, "mn", Mean, Cov) génère n réalisations indépendantes de la loi multi-normale ; Mean doit être un vecteur colonne m x 1, et Cov une matrice carrée m x m symétrique et définie positive. Y est alors une matrice m x n.

geometrique

Y = grand(m, n, "geom", p) génère des nombres aléatoires suivant la loi geométrique de paramètre p : nombre d'épreuves de Bernouilli (de probabilité de succès p) jusqu'à obtenir un succès (avec p dans [1.3e-307, 1]).

Y contient des nombres réels positifs à valeur entière qui sont "le nombre de tentatives nécessaire pour obtenir un succès" pour chaque tirage.

markov

Y = grand(n, "markov", P, x0) génère n états successifs d'une chaîne Markov décrite par la matrice de transition P. L'état initial est donné par x0. Si x0 est une matrice de taille m = size(x0, "*") alors Y est une matrice de taille m x n. Y(i,:) est le chemin à partir de l'état initial x0(i).

multinomiale

Y = grand(n, "mul", nb, P) génère n réalisations indépendantes de la loi multinomiale : classer nb éventualités dans m catégories (mettre nb "boules" dans m "boites"). P(i) est la probabilité qu'une éventualité soit de categorie i. P le vecteur des probabilités est de taille m-1 (la probabilté de la catégorie m étant 1-sum(P)). Y est alors de dimensions m x n, chaque colonne Y(:,j) étant une réalisation de cette loi : Y(i,j) est le nombre d'éventualités classées en catégorie i pour la j ème réalisation (sum(Y(:,j)) = nb).

Poisson

Y = grand(m, n, "poi", mu) génère des nombres aléatoires suivant la loi de Poisson de moyenne mu (réel >= 0.0). Fonction associée : cdfpoi.

permutations aléatoires

Y = grand(n, "prm", array) produit n permutations aléatoires des éléments de array. array peut être un vecteur, une matrice ou une hypermatrice de nombres réels ou complexes, d'entiers, booléens, polynômes ou textes ; dense ou creuse.

• Si array est un vecteur ligne 1 x m, Y est une matrice n x m.
• Si array est un vecteur colonne m x 1, Y est une matrice m x n.
• Si array est une matrice m x p, Y est une hypermatrice m x p x n.
• If array une hypermatrice m x p x q…, Y est une hypermatrice m x p x q… x n.

La fonction randperm(n) d'Octave est équivalente à grand(1,'prm', 1:n), et randperm(n, k) est réalisé par Scilab avec grand(1,'prm', 1:n)(1:k).

uniforme (def)

Y = grand(m, n, "def") génère des nombres aléatoires suivant la loi uniforme sur [0,1[ (1 n'est jamais produit).

uniforme (unf)

Y = grand(m, n, "unf", Low, High) génère des nombres aléatoires suivant la loi uniforme sur [Low, High[ (High n'est jamais atteint).

uniforme (uin)

Y = grand(m, n, "uin", Low, High) génère des entiers aléatoires suivant la loi uniforme sur [Low, High]. High et Low doivent être des entiers tels que (High-Low+1) < 2147483561 .

uniforme (lgi)

Y = grand(m, n, "lgi") retourne la sortie du générateur de base courant : des entiers aléatoires suivant une loi uniforme sur :

• [0, 2^32 - 1] for mt and kiss;

• [0, 2147483561] for clcg2;

• [0, 2^31 - 2] for clcg4;

• [0, 2^31 - 1] for urand.

Actions sur le(s) générateur(s) de base

Depuis Scilab-2.7 vous avez la possibilité de choisir parmi plusieurs générateurs de base (donnant des entiers aléatoires suivant la loi "lgi") :

mt

Le Mersenne-Twister de M. Matsumoto and T. Nishimura, période d'environ 2^19937, état interne donné par 624 entiers (plus un index); c'est le générateur par défaut.

kiss

Le Keep It Simple Stupid de G. Marsaglia, période d'environ 2^123, état interne donné par 4 entiers.

clcg2

Une combinaison de 2 générateurs linéaires congruentiels de P. L'Ecuyer, période d'environ 2^61, état interne donné par 2 entiers ; c'était le seul générateur de base utilisé auparavent par grand (cette version est cependant légèrement différente de l'ancienne).

clcg4

Une combinaison de 4 générateurs linéaires congruentiels de P. L'Ecuyer, période d'environ 2^121, état interne donné par 4 entiers ; ce générateur peut être partagé en 101 générateur virtuels (en fait la suite de longueur 2^121 peut être découpée en 101 sous-suites) ce qui peut être utile dans certains cas (voir 'Actions specifiques à clcg4' et 'Exemple d'utilisation de clcg4').

urand

Le générateur de base utilisé par la fonction rand, état interne constitué d'un entier, période de 2^31. Ce generateur est fondé sur "Urand, A Universal Random Number Generator" By, Michael A. Malcolm, Cleve B. Moler, Stan-Cs-73-334, January 1973, Computer Science Department, School Of Humanities And Sciences, Stanford University. C'est le plus rapide de cette liste, mais ses qualités statistiques sont inférieures aux autres générateurs.

Actions

action = "getgen"

S = grand("getgen") retourne le nom du générateur de base actuel (S est l'une des chaînes de caractères "mt", "kiss", "clcg2", "clcg4", "urand").

action = "setgen"

grand("setgen", gen) permet de changer le générateur de base : gen doit être l'une des chaînes de caractères "mt", "kiss", "clcg2", "clcg4", "urand". En cas de succès la fonction retourne cette même chaîne.

action = "getsd"

S = grand("getsd") retourne l'état interne actuel (les 'germes' dans l'ancienne appelation quoique ce terme désigne plutôt l'état initial) du générateur de base courant ; S est un vecteur colonne (d'entiers) de dimension 625 pour mt (la première composante étant un 'index' sur l'état, c-a-d un entier de l'intervalle [1,624]), 4 pour kiss, 2 pour clcg2 , 4 pour clcg4 (pour ce dernier vous obtenez l'état interne du générateur virtuel courant), et 1 pour urand.

action = "setsd"

grand("setsd", S), grand("setsd", s1[, s2, s3, s4]) impose l'état interne du générateur de base courant :

pour mt

S est un vecteur d'entiers de dimension 625 (la première composante étant un index sur [1,624]), les 624 dernières composantes doivent être dans [0,2^32[) (mais ne doivent pas être toutes nulles) ; une initialisation plus simple est possible (et recommandée) en donnant un seul entier s1 (s1 appartenant à [0,2^32[) ;

pour kiss

4 entiers s1, s2, s3, s4 dans [0,2^32[ doivent être fournis ;

pour clcg2

2 entiers s1 dans [1, 2147483562] et s2 dans [1, 2147483398] doivent être fournis ;

pour clcg4

4 entiers s1 dans [1, 2147483646], s2 dans [1, 2147483542], s3 dans [1, 2147483422], s4 dans [1, 2147483322] sont requis ; ATTENTION : avec clcg4 vous positionnez l'état interne du générateur virtuel courant mais vous perdez alors la synchronisation avec les autres générateurs virtuels. (=> si vous utilisez clcg4 avec différents générateurs virtuels, il faut utiliser l'option "setall" qui permet de changer l'état interne (du générateur numéro 0) tout en recalculant l'état initial des 100 autres générateurs virtuels).

pour urand

1 entier s1 appartenant à [0, 2^31[ est requis.

action = "phr2sd"

Sd = grand("phr2sd", phrase) étant donnée une chaîne de caractères phrase cet appel retourne un vecteur 1 x 2 qui peut être utilisé comme état interne pour un générateur de base (initialement adapté pour clcg2).

Options specifiques à clcg4

Le générateur clcg4 peut être utilisé comme les autres mais il offre l'avantage de pouvoir être découpé en (101) générateurs virtuels différents, c-a-d avec des séquences sans intersection (quand vous utilisez un générateur classique vous pouvez changer l'état initial de façon à obtenir une autre séquence mais vous n'êtes pas complètement sûr d'obtenir une séquence complètement différente). Chaque générateur virtuel correspond à une séquence de longueur 2^72 qui est de plus découpée en V = 2^31 segments de longueur W = 2^41. Pour un générateur virtuel donné vous pouvez retourner au début de la séquence ou au début du segment ou bien au début du segment suivant. Vous pouvez aussi changer l'état initial du générateur 0 avec l'option "setall" qui recalcule l'état initial des autres générateurs virtuels de sorte à obtenir la synchronisation entre les générateurs (c-a-d qu'en fonction du nouvel état initial du générateur 0 l'état initial des générateurs 1..100 sont recalculés de façon à obtenir 101 séquences qui ne s'intersectent pas).

action = "setcgn"

grand("setcgn", G) sélectionne le générateur virtuel numéro G : lorsque le générateur de base courant est clcg4, c'est le générateur virtuel G qui sera alors utilisé ; les 101 générateurs virtuels sont numérotés 0,1,...,100 (ainsi G doit être un entier de l'intervalle [0, 100]) ; par défaut le générateur virtuel courant est celui de numéro 0.

action = "getcgn"

S = grand("getcgn") retourne le numéro du générateur virtuel courant.

action = "initgn"

grand("initgn", I) réinitialise l'état du générateur virtuel courant :

I = -1

remet l'état à sa valeur initiale

I = 0

remet l'état au début du segment courant

I = 1

positionne l'état au début du segment suivant et met à jour les valeurs définissant le segment courant (vous ne pouvez pas revenir au début du segment précédent).

action = "setall"

grand("setall", s1, s2, s3, s4) impose l'état interne du générateur virtuel de numéro 0 à s1, s2, s3, s4. L'état initial des autres générateurs est alors reconstruit (de façon à obtenir 101 séquences qui ne s'intersectent pas). Voir l'action "setsd" pour les contraintes sur s1, s2, s3, s4.

action = "advnst"

grand("advnst", K) avance l'état du générateur virtuel courant de 2^K valeurs et réinitialise l'état initial (du générateur virtuel courant) à ce nouvel état.

Exemples

Dans l'exemple suivant, nous produisons des nombres aléatoires associés à différentes lois de distribution et dessinons les histogrammes associés.

// Renvoie une matrice de taille 400 x 800 de doubles aléatoires,
// avec une distribution normale de moyenne 0 et d'écart-type 1.
R = grand(400, 800, "nor", 0, 1);
scf();
histplot(10, R);
xtitle("Nombres aléatoires (loi normale) par grand", "X", "Fréquence");

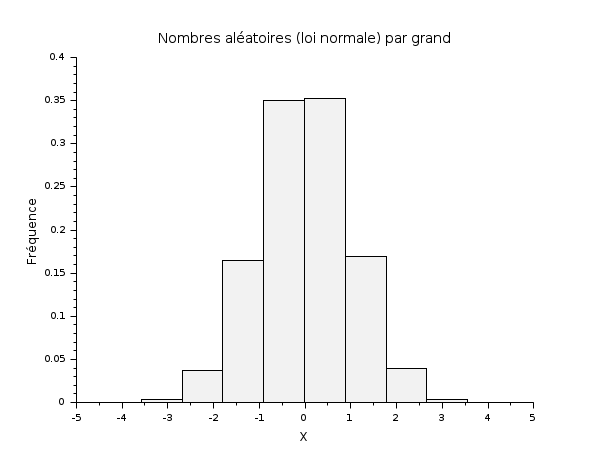
// Renvoie une matrice de taille 400 x 800 de doubles aléatoires,
// uniformes dans [0, 1).
R = grand(400, 800, "def");
scf();
histplot(10, R);
xtitle("Nombres aléatoires uniformes par grand", "X", "Fréquence");

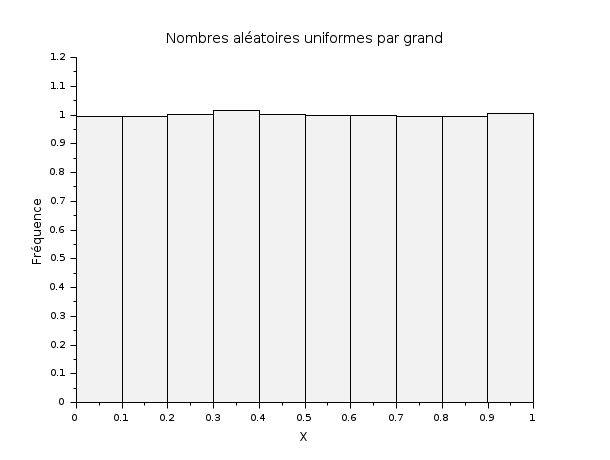
// Renvoie une matrice de taille 400 x 800 de doubles aléatoires,
// avec une distribution de Poisson de moyenne 5.
R = grand(400, 800, "poi", 5);
scf();
histplot(10, R);
xtitle("Nombres aléatoires (loi de Poisson) par grand", "X", "Fréquence");

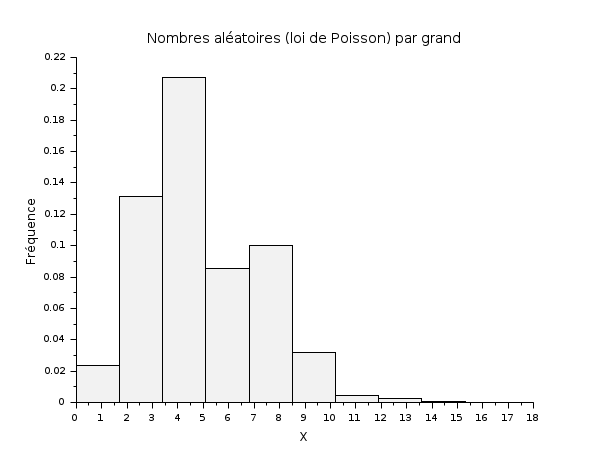
Dans l'exemple suivant, nous produisons des nombres aléatoires suivant la loi exponentielle et comparons ensuite la distribution empirique et la fonction de distribution théorique.

lambda = 1.6;
N = 100000;
X = grand(1, N, "exp", lambda);
scf();
classes = linspace(0, 12, 25);
histplot(classes, X);
x = linspace(0, 12, 25);
y = (1/lambda)*exp(-(1/lambda)*x);
plot(x, y, "ro-");
legend(["Empirique" "Theorique"]);
xtitle("Loi exponentielle par grand", "X", "Fréquence");

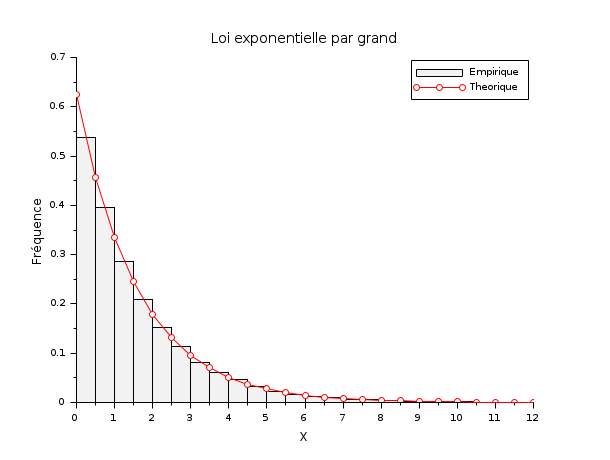
Dans l'exemple suivant, nous générons des nombres aléatoires selon la distribution gamma et comparons la distribution empirique et la loi de distribution théorique.

N = 10000;
A = 10;
B = 4;
R = grand(1, N, "gam", A, B);
XS = gsort(R, "g", "i")';
PS = (1:N)'/N;
P = cdfgam("PQ", XS, A*ones(XS), B*ones(XS));
scf();
plot(XS, PS, "b-"); // Empirical distribution
plot(XS, P, "r-"); // Theoretical distribution
legend(["Empirique" "Théorique"]);
xtitle("Fonction de distribution cumulée de nombres aléatoires selon la loi Gamma", "X", "F");

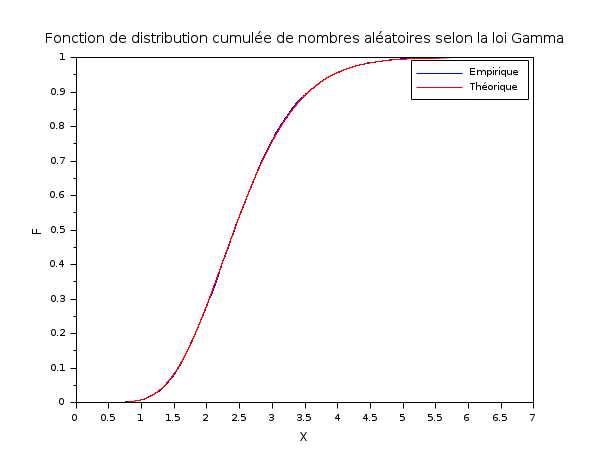
Dans l'exemple suivant, nous générons 10 entiers aléatoires dans l'intervalle [1, 365].

grand(10, 1, "uin", 1, 365)

Dans l'exemple suivant, nous générons 12 permutations de l'ensemble [1,2,...,7]. Les 12 permutations sont stockées colonne par colonne.

grand(12, "prm", (1:7)')

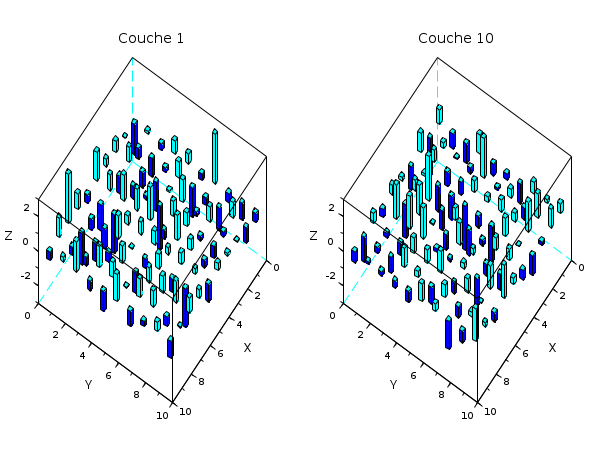
L'exemple suivant génère une hypermatrice 10-par-10-par-10 de nombre aléatoires provenant de la distribution "normale" et affiche les histogrammes associés. Le graphes montrent les première et dernière couches de la matrice.

// Retourne une hypermatrice 400 x 800 x 10 de nombre aléatoires,
// avec la distribution normale, une moyenne de 0 et un écart-type de 1.
// Affichage de la première et dernière couches.
R = grand(10,10,10,"nor",0,1);
subplot(1,2,1)
bar3d(R(:,:,1));
xtitle("Couche 1");
subplot(1,2,2)
bar3d(R(:,:,10));
xtitle("Couche 10");

Produire des nombres prévisibles ou moins prévisibles

Les générateurs pseudo aléatoires sont fondés sur des séquences déterministes. Pour produire des simulations reproductibles, la graine du générateur est constante, de telle sorte que la séquence est la même d'une session à l'autre. En conséquence, par défaut, les premiers nombres produis par grand sont toujours les mêmes.

Dans certaines situations, nous peut vouloir initialiser la graine du générateur dans le but de produire des nombres moins prédictibles. Dans ce cas, on peut initialiser la graine avec la sortie de la fonction getdate :

n = getdate("s");
grand("setsd", n)

Exemple d'utilisation de clcg4

On cherche à comparer deux techniques statistiques sur des données de tailles différentes. La première, utilisant le 'bootstrapping' est supposée a priori aussi précise que la deuxième technique (utilisant uniquement la force brute) tout en utilisant moins de données. Pour la première méthode, un ensemble de données de taille n1, uniformément distribuée entre 25 et 50 devra être généré puis analysé par la méthode. Pour la seconde méthode, on procède de même avec une taille n2 à choisir entre 100 et 200. Ce processus est répété 1000 fois. Pour la réduction de la variance, on veut que les nombres aléatoires utilisés dans les deux méthodes soient les mêmes pour chacune des 1000 comparaisons. Comme la deuxième méthode utilise plus de nombres aléatoires, la synchronisation peut être difficile si l'on utilise un générateur classique. Avec un générateur comme clcg4 c'est par contre très simple : utilisez le générateur 0 pour obtenir la taille n1 du jeux de données et le générateur 1 pour obtenir les données. Avec le générateur 0 tirer la taille n2 puis resélectionner le générateur 1 et revenez au début du segment courant pour obtenir les n2 données pour la deuxième méthode : ainsi les données initiales (les n1 premieres) sont les mêmes pour les deux méthodes. Pour la comparaison suivante, il suffit d'avancer le générateur 1 au segment suivant, etc...

Voir aussi

• rand — Générateur de nombres pseudo-aléatoires
• sprand — matrice creuse aléatoire
• ssrand — random system generator
• randpencil — random pencil
• genmarkov — generates random markov matrix with recurrent and transient classes