beta
função beta
Seqüência de Chamamento
z = beta(x,y)
Parâmetros
- x, y
dois reais positivos ou duas matrizes (ou vetores) de reais positivos de mesmo tamanho
- z
um real ou uma matriz de reais com mesmo tamanho que
xcomz(i,j) = beta(x(i,j),y(i,j)).
Descrição
Computa a função beta completa :
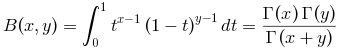
Para x e y pequenos, o
algoritmo usa a expressão em função da função gama, de outro modo, ele
aplica a função exponencial no resutado da função
betaln function fornecido no DCDFLIB: Biblioteca de
Rotinas FORTRAN para Funções, Inversas e Outros Parâmetros de Distribuição
Cumulativa (ver cdfbet para maiores
informações sobre DCDFLIB).
Exemplos
// exemplo 1 : beta(5,2) - beta(2,5) // simetria (deve ser exatamente 0) beta(0.5,0.5) // o valor exato é pi // exemplo 2 : um estudo de erros baseado na relação B(1,x) = 1/x // (a computação de 1/x deve levar apenas a um erro relativo de eps_m, então // pode ser usada como referência para avaliar o erro em B(1,x)) x = logspace(-8,8,20000)'; e = beta(ones(x),x) - (1)./x; er = abs(e) .* x; ind = find(er ~= 0); eps = ones(x(ind))*number_properties("eps"); clf() plot2d(x(ind),[er(ind) eps 2*eps],style=[1 2 3],logflag="ll",leg="er@eps_m@2 eps_m") xtitle("erro relativo aproximado na computação de beta(1,x)") show_window() // exemplo 3 : plotando a função beta t = linspace(0.2,10,60); X = t'*ones(t); Y = ones(t')*t; Z = beta(X,Y); clf() plot3d(t, t, Z, flag=[2 4 4], leg="x@y@z", alpha=75, theta=30) xtitle("A função beta em [0.2,10]x[0.2,10]") show_window()
Ver Também
| Report an issue | ||
| << besseli | Funções Especiais | calerf >> |