beta
ベータ関数 (第1種オイラー積分)
呼び出し手順
z = beta(x,y)
パラメータ
- x, y
正の実数または同じ大きさの正の実数の行列(ベクトル).
- z
実数または
z(i,j) = beta(x(i,j),y(i,j))となるxと同じ大きさの行列.
説明
完全ベータ関数を計算します :
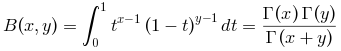
x およびyが小さい場合,
このアルゴリズムは,関数内でガンマ関数の式を使用します.
そうでない場合はDCDFLIBにより提供される
betaln関数の結果に指数関数を適用します:
DCDFLIBは累積密度関数,逆,およびその他のパラメータに関する
Fortranルーチンのライブラリです
(DCDFLIBに関する詳細については cdfbet を参照
).
例
// 例 1 : beta(5,2) - beta(2,5) // 対称性 (0になります) beta(0.5,0.5) // 値はpiになります
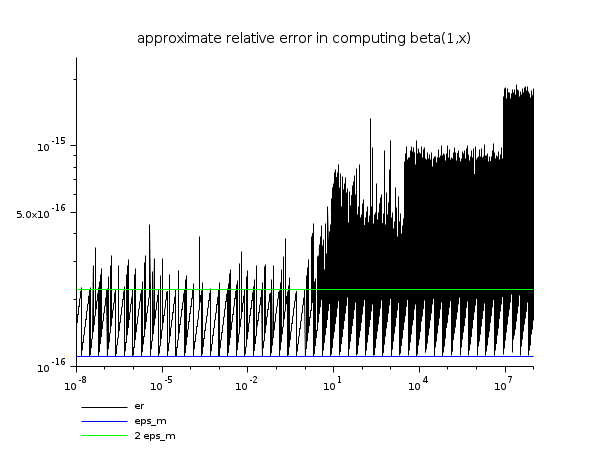
// 例 2 : 関係 B(1,x) = 1/xに基づく誤差解析 // (1/x の計算は eps_mの相対誤差のみを発生するため, // B(1,x)の誤差を評価する際の基準として使用できます) x = logspace(-8,8,20000)'; e = beta(ones(x),x) - (1)./x; er = abs(e) .* x; ind = find(er ~= 0); eps = ones(x(ind))*number_properties("eps"); clf() plot2d(x(ind),[er(ind) eps 2*eps],style=[1 2 3],logflag="ll",leg="er@eps_m@2 eps_m") xtitle("approximate relative error in computing beta(1,x)") show_window()
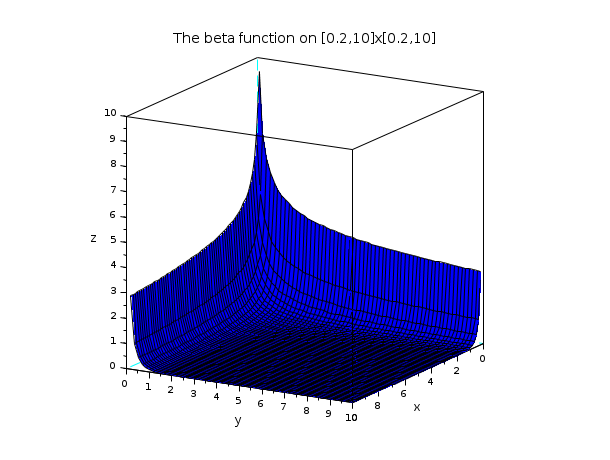
// 例 3 : ベータ関数をプロット t = linspace(0.2,10,60); X = t'*ones(t); Y = ones(t')*t; Z = beta(X,Y); clf() plot3d(t, t, Z, flag=[2 4 4], leg="x@y@z", alpha=75, theta=30) xtitle("The beta function on [0.2,10]x[0.2,10]") show_window()
| Report an issue | ||
| << besseli | Special Functions | calerf >> |