besseli
funções modificadas de Bessel do primeiro tipo (Iα).
besselj
funções de Bessel do primeiro tipo (Jα).
besselk
funções modificadas de Bessel do segundo tipo (Kα).
bessely
funções de Bessel do segundo tipo (Yα).
besselh
funções de Bessel do terceiro tipo (também conhecidas como funções de Hankel)
Seqüência de Chamamento
y = besseli(alpha, x [,ice]) y = besselj(alpha, x [,ice]) y = besselk(alpha, x [,ice]) y = bessely(alpha, x [,ice]) y = besselh(alpha, x) y = besselh(alpha, K, x [,ice])
Parâmetros
- x
vetor de reais ou complexos
- alpha
vetor de reais
- ice
flag (sinalizador) inteiro, com valor padrão 0
- K
inteiro, com valores possíveis 1 ou 2, a função do tipo de Hankel.
Descrição
besseli(alpha,x)computa as funções de Bessel modificadas do primeiro tipo (Iα), para ordem realalphae argumentox.besseli(alpha,x,1)computabesseli(alpha,x).*exp(-abs(real(x))).besselj(alpha,x)computa as funções de Bessel do primeiro tipo (Jα), para ordem realalphae argumentox.besselj(alpha,x,1)computabesselj(alpha,x).*exp(-abs(imag(x))).besselk(alpha,x)computa as funções de Bessel modificadas do segundo tipo (Kα), para ordem realalphae argumentox.besselk(alpha,x,1)computabesselk(alpha,x).*exp(x).bessely(alpha,x)computa as funções de Bessel do segundo tipo (Yα), para ordem realalphae argumentox.bessely(alpha,x,1)computabessely(alpha,x).*exp(-abs(imag(x))).besselh(alpha [,K] ,x)computa as funções de Bessel do terceiro tipo (função de Hankel H1 ou H2, dependendo doK), para ordem realalphae argumentotx. Se omitido,Ké suposto como sendo 1.besselh(alpha,1,x,1)computabesselh(alpha,1,x).*exp(-%i*x)ebesselh(alpha,2,x,1)computabesselh(alpha,2,x).*exp(%i*x)
Observações
Se alpha e x são arrays de
mesmo tamanho, o resultado y também terá este tamanho.
Se uma entrada é um escalar, ela é expandida para o tamanho da outra
entrada. Se uma entrada é um vetor linha e a outra é um vetor coluna, o
resultado y é um table 2-dimensional ("tabela") de
valores de funções.
As funções de Bessel Yα e Jα são duas soluções independentes da equação diferencial de Bessel:
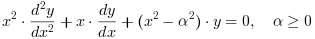
As funções modificadas de Bessel Kα e Iα são duas soluções independentes para a equação diferencial de Bessel :
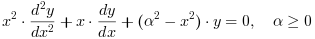
As funções de Hankel de primeiro e segundo tipos H2α e H2α, são combinações lineares das funções de Bessel de primeiro e segundo tipos:
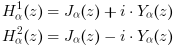
Exemplos
// Funções I de Bessel // ================== x = linspace(0.01,10,5000)'; clf() subplot(2,1,1) plot2d(x,besseli(0:4,x), style=2:6) legend('I'+string(0:4),2); xtitle("Algumas funções modificadas de Bessel do primeiro tipo") subplot(2,1,2) plot2d(x,besseli(0:4,x,1), style=2:6) legend('I'+string(0:4),1); xtitle("Algumas funções modificadas de Bessel do primeiro tipo escaladas")
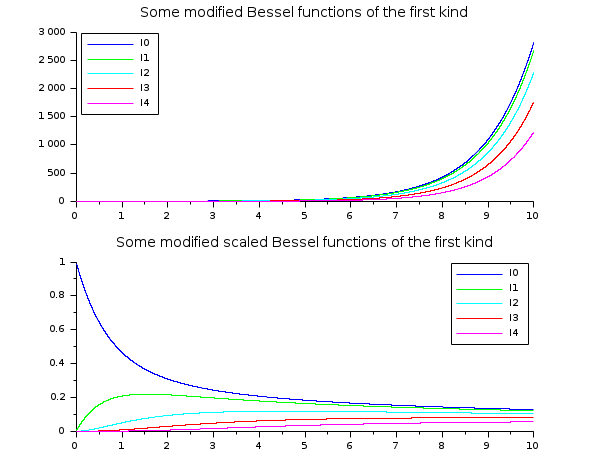
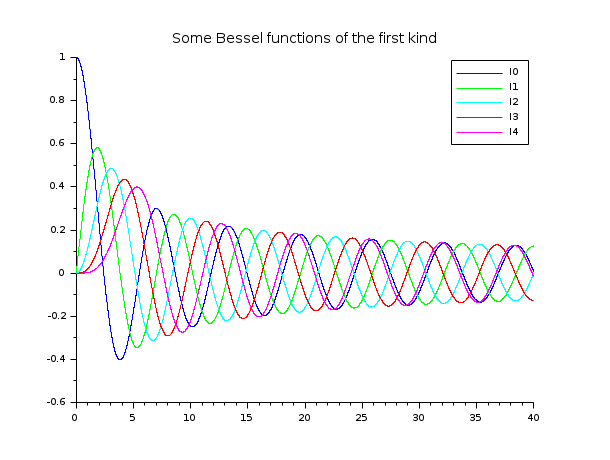
// Funções J de Bessel // ================= x = linspace(0,40,5000)'; clf() plot2d(x,besselj(0:4,x), style=2:6, leg="J0@J1@J2@J3@J4") legend('I'+string(0:4),1); xtitle("Algumas funções de Bessel do primeiro tipo")
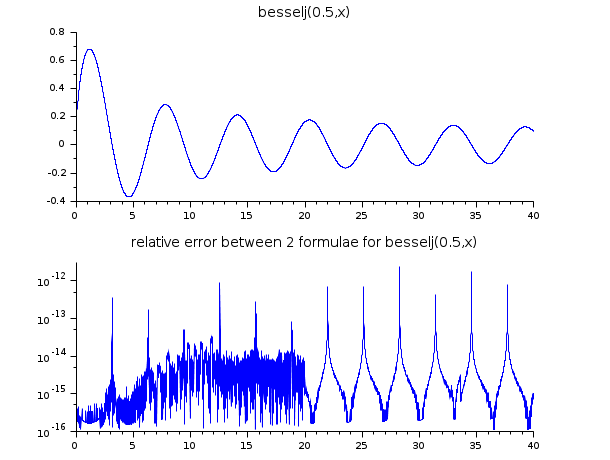
// Usando o fato de que J_(1/2)(x) = sqrt(2/(x pi)) sin(x) // Para comparar o algoritmo de besselj(0.5,x) com uma fórmula mais direta x = linspace(0.1,40,5000)'; y1 = besselj(0.5, x); y2 = sqrt(2 ./(%pi*x)).*sin(x); er = abs((y1-y2)./y2); ind = find(er > 0 & y2 ~= 0); clf() subplot(2,1,1) plot2d(x,y1,style=2) xtitle("besselj(0.5,x)") subplot(2,1,2) plot2d(x(ind), er(ind), style=2, logflag="nl") xtitle("Erro relativo entre as duas fórmulas para besselj(0.5,x)")
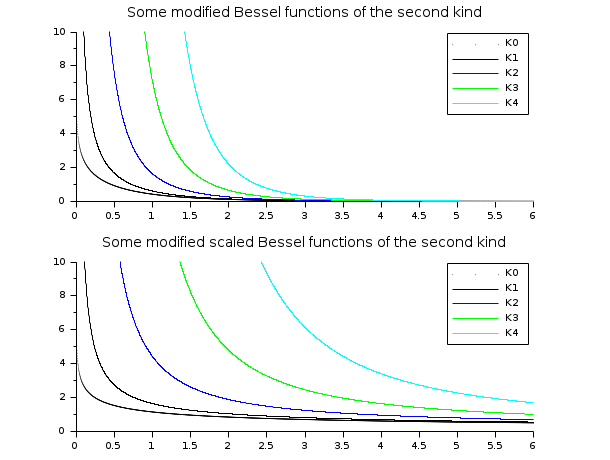
// Funções K de Bessel // ================= x = linspace(0.01,10,5000)'; clf() subplot(2,1,1) plot2d(x,besselk(0:4,x), style=0:4, rect=[0,0,6,10]) legend('K'+string(0:4),1); xtitle("Algumas funções modificadas de Bessel do segundo tipo") subplot(2,1,2) plot2d(x,besselk(0:4,x,1), style=0:4, rect=[0,0,6,10]) legend('K'+string(0:4),1); xtitle("Algumas funções modificadas de Bessel do segundo tipo escaladas")
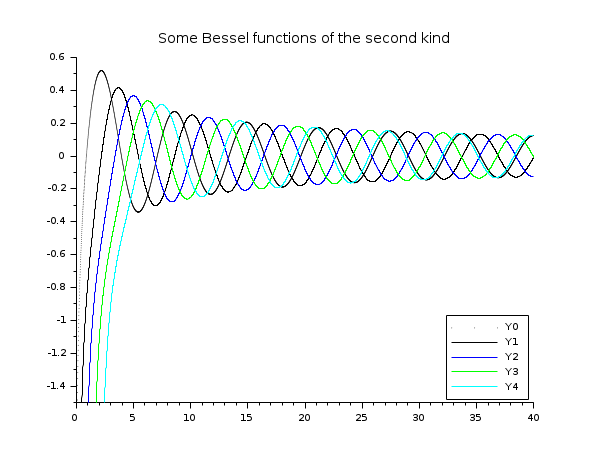
// Funções Y de Bessel // ================= x = linspace(0.1,40,5000)'; // funções Y de Bessel não possuem limite para x -> 0+ clf() plot2d(x,bessely(0:4,x), style=0:4, rect=[0,-1.5,40,0.6]) legend('Y'+string(0:4),4); xtitle("Algumas funções de Bessel do segundo tipo")
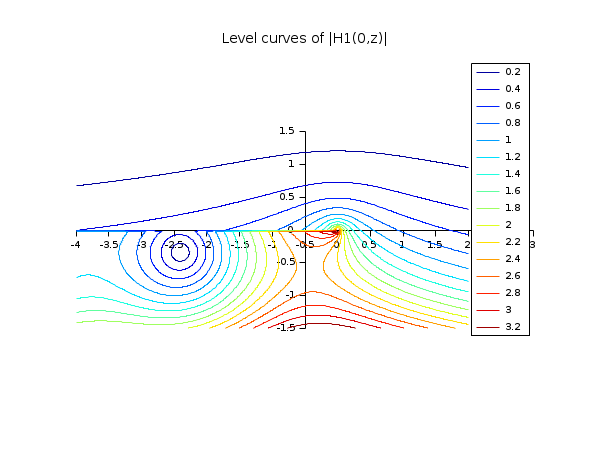
// Funções H de Bessel // ================= x=-4:0.025:2; y=-1.5:0.025:1.5; [X,Y] = ndgrid(x,y); H = besselh(0,1,X+%i*Y); clf();f=gcf(); f.color_map=jetcolormap(16); contour2d(x,y,abs(H),0.2:0.2:3.2,strf="034",rect=[-4,-1.5,3,1.5],fpf=" ") legends(string(0.2:0.2:3.2),1:16,"ur") xtitle("Curvas de nível de |H1(0,z)|")
Autores
- Amos, D. E., (SNLA)
- Daniel, S. L., (SNLA)
- Weston, M. K., (SNLA)
Função Usada
Os códigos-fontes podem ser achados em SCI/modules/special_functions/src/fortran/slatec e SCI/modules/special_functions/src/fortran
Slatec : dbesi.f, zbesi.f, dbesj.f, zbesj.f, dbesk.f, zbesk.f, dbesy.f, zbesy.f, zbesh.f
Drivers para estender a área de definição (Serge Steer INRIA): dbesig.f, zbesig.f, dbesjg.f, zbesjg.f, dbeskg.f, zbeskg.f, dbesyg.f, zbesyg.f, zbeshg.f
| Report an issue | ||
| << amell | Funções Especiais | beta >> |