householder
Matrice de Householder. Symétrique par rapport à un plan
Séquence d'appel
householder // demo u = householder(v [,w]) [u, H] = householder(v [,w])
Paramètres
- v
vecteur colonne réel ou complexe
- w
vecteur colonne réel ou complexe de même taille que
vLa valeur par défaut esteye(v)(axe (Ox)).- u
vecteur unitaire résidant dans le plan
(v,w)et orthogonal à la bissectrice de(v,w). Colonne de nombres réels ou complexes, de taille size(v).- H
Matrice orthogonale de réflexion de Householder :
H= eye() - 2*u*u'.Hest telle queinv(H)==H,H'==H, etdet(H)==-1.Si
vetwsont des vecteurs réels,H*vest colinéaire àw.
Description
householder(..) calcule le vecteur unitaire u
résidant dans le plan (v,w) et orthogonal à la bissectrice de
(v,w).
Si v et w sont proportionels :
- S'ils sont opposés,
u= v/|v|est retourné. - S'ils sont à coordonnées réelles et sont dans la même direction,
uest choisi dans le plan (xOy) avec a prioriu(1)>0, et orthogonal àv(u'*v==0). Cependant,- S'ils sont selon (Ox),
u = (Oy+)est retourné. - S'ils sont scalaires (et de mêmes signes),
le sous-espace orthogonal est réduit à
{0}qui n'est pas normalisable :uetHsont mis à%nan.
- S'ils sont selon (Ox),
 | Si la matrice de réflexion H correspondante est calculée,
pour tout point A de coordonnées a en colonne, H*a
sont les coordonnées du symétrique de A par rapport au plan (v,w)
(exemple ci-dessous). |
 | Si v ou/et w sont des vecteurs ligne,
ils sont préalablement transposés en colonnes. |
 | Si v ou/et w sont [],
u et H valent alors []. |
Exemples
a = [ rand(1,1) 0 0 ]'; [ra hm] = householder(a); [a ra hm*a ] norm(ra) b = rand(3,1); [rb, hm] = householder(b); [b rb eye(b) clean(hm*b) ] norm(rb) [rb2b, hm] = householder(b, 2*b); [b rb2b clean(hm*b ./ b) ] // la dernière colonne doit être uniforme norm(rb2b) // doit valoir 1 c = rand(3,1); [rbc, hm] = householder(b,c); norm(rbc) // doit valoir 1 hm*b ./c // doit être uniforme d = b + %i*c; e = rand(3,1) + %i*rand(3,1); [rde, hm] = householder(d,e); norm(rbc) // doit valoir 1 clean(inv(hm) - hm) // doit valoir zeros(3,3) clean(hm' - hm) // doit valoir zeros(3,3) clean(det(hm)) // doit valoir -1
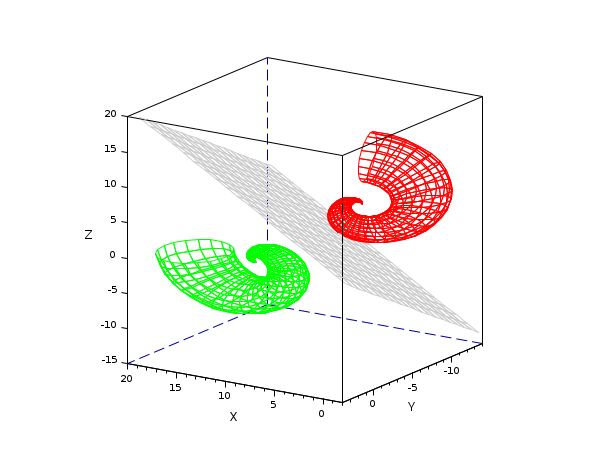
Application : Symétrique d'un objet par rapport à un plan donné.
// (OA) = [0 0 1] se réfléchit en O en (OB) = [ 1 1 0.3 ]: [n, H] = householder([0 0 1]', [ 1 1 0.3 ]'); // "n" est la normale au plan "réflecteur" // Objet source : u = linspace(0,2*%pi,40); v = linspace(0,2*%pi,20); Xe = (cos(u).*u)'*(1+cos(v)/2)+10; Ye = (u/2)'*sin(v); Ze = (sin(u).*u)'*(1+cos(v)/2); // Image symétrique de l'objet : P = [ Xe(:)' ; Ye(:)' ; Ze(:)']; Pr = H*P; Xr = matrix(Pr(1,:),40,-1); Yr = matrix(Pr(2,:),40,-1); Zr = matrix(Pr(3,:),40,-1); // Plan réflecteur contenant O : n(1).x + n(2).y + n(3).z = 0: // Grille d'espace : x = linspace(min([Xe(:);Xr(:)]), max([Xe(:);Xr(:)]),20); y = linspace(min([Ye(:);Yr(:)]), max([Ye(:);Yr(:)]),20); [X, Y] = meshgrid(x,y); // Création du plan: deff("z = mirror(x,y,n)","z = -n(1)/n(3)*x - n(2)/n(3)*y") Zm = mirror(X,Y,n); // Illustration graphique : clf() isoview() drawlater() f = gcf(); f.color_map = [ 0.8 0.8 0.8 ; jetcolormap(100)]; surf(Xe,Ye,Ze) surf(X,Y,Zm) surf(Xr,Yr,Zr) a = gca(); a.rotation_angles = [74 123]; a.children.color_flag = 0; a.children.color_mode = 0; a.children(1).foreground = color("red"); a.children(2).foreground = 1; a.children(3).foreground = color("green"); drawnow()
Voir aussi
Historique
| Version | Description |
| 6.0 | Matrice de réflexion de Householder fournie en second paramètre de sortie. Demo householder() ajoutée. Page d'aide revue. |
| Report an issue | ||
| << givens | Algèbre Lineaire | proj >> |