Scilab Website | Contribute with GitLab | Mailing list archives | ATOMS toolboxes
Scilab Online Help
2023.0.0 - 日本語


dct

離散コサイン変換.

idct

逆離散コサイン変換.

呼び出し手順

X = dct(A)
X = dct(A, sign)
X = dct(A, sign, selection)
X = dct(A, sign, dims, incr)
X = dct(.., option)

X = idct(A)
X = idct(A, selection)
X = idct(A, dims, incr)
X = idct(.., option)

引数

A

実数/複素ベクトルまたは実数/複素配列 (ベクトル, 行列または N-D 配列).

X
Aと同じ大きさの 実数または複素配列.
sign
整数.値は 1または -1となります. 順方向または逆変換を選択します. デフォルト値は-1 (順方向変換)です.
selection
Aの各配列次元への添字を有する ベクトル. 詳細は説明を参照ください.
dims
整数値を有する正の数値ベクトル, または正の整数のベクトル. 詳細は説明を参照ください.

各要素は Aの要素の総数の約数となります.

各要素の積はAの要素の総数よりも 小さな値とする必要があります.

incr
整数値を有する正の数値ベクトル, または正の整数のベクトル. 詳細は説明を参照ください.

incr は, dimsの要素数と同じにする 必要があります.

各要素は,Aの要素の総数の約数とする 必要があります.

incr の要素は, 厳密に昇順とする必要があります.

option
文字列. 値は,順方向変換の場合, "dct1", "dct2", "dct4" または "dct", 逆変換の場合は "dct1", "dct3", "dct4"または "idct" です. デフォルト値は,順方向変換の場合に"dct", 逆変換の場合に"idct"です. 詳細は説明を参照ください.

説明

変換の説明

この関数は, パラメータ値optionで指定したシフト量を用いて 順方向または逆方向の1次元またはN次元離散コサイン変換を 行います. 長さnの1次元配列Aの場合:

  • "dct1"の場合, この関数は 正規化しないDCT-I変換を計算します: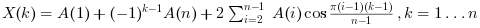

    $X(k) = A(1) + (-1)^{k-1}A(n) + 2\sum_{i=2}^{n-1} {A(i) \cos\frac{\pi (i -1)(k-1)}{n-1}}, k=1\ldots n$

  • "dct2"の場合,この関数は 正規化しないDCT-II変換を計算します: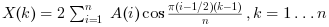

    $X(k) = 2 \sum_{i=1}^{n} {A(i) \cos\frac{\pi (i -1/2)(k-1)}{n}}, k=1\ldots n$

  • "dct3"の場合,この関数は 正規化しないDCT-III変換を計算します: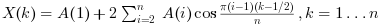

    $X(k) = A(1) + 2 \sum_{i=2}^{n} {A(i) \cos\frac{\pi (i -1)(k-1/2)}{n}}, k=1\ldots n$

  • "dct4"の場合,この関数は 正規化しないDCT-IV変換を計算します: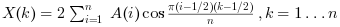

    $X(k) = 2 \sum_{i=1}^{n} {A(i) \cos\frac{\pi (i -1/2)(k-1/2)}{n}}, k=1\ldots n$

  • "dct"の場合,この関数は 正規化されたDCT-II変換を計算します: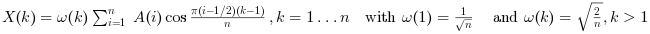

    $X(k) = \omega(k) \sum_{i=1}^n {A(i) \cos\frac{\pi (i -1/2)(k-1)}{n}}, k=1\ldots n \quad\text{with } \omega(1)=\frac{1}{\sqrt{n}} \quad\text{and } \omega(k)=\sqrt{\frac{2}{n}} , k>1$

  • "idct"の場合,この関数は 正規化されたDCT-III変換を計算します: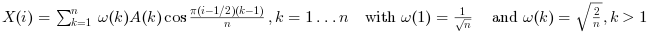

    $X(i) = \sum_{k=1}^n {\omega(k) A(k) \cos\frac{\pi (i -1/2)(k-1)}{n}}, k=1\ldots n \quad\text{with } \omega(1)=\frac{1}{\sqrt{n}} \quad\text{and } \omega(k)=\sqrt{\frac{2}{n}} , k>1$

多次元のDCT変換は,一般に, 配列の各次元方向の1次元変換の分離可能な積です. 正規化しない変換の場合, 順方向の後に逆方向多次元変換を行うと, 元の配列が各次元の大きさの積で拡大されたものと なります.

次元がn1, n2, …, npの 配列Aの正規化された多次元DCT変換 は以下のように計算されます

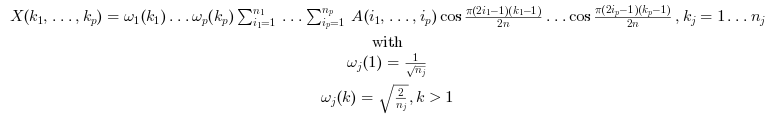
$\begin{array} \\X(k_1, \dots, k_p) = \omega_1(k_1) \ldots \omega_p(k_p) \sum_{i_1=1}^{n_1} \ldots \sum_{i_p=1}^{n_p} {A(i_1,\ldots ,i_p) \cos\frac{\pi (2 i_1 -1)(k_1-1)}{2 n} \ldots \cos\frac{\pi (2 i_p -1)(k_p-1)}{2 n}}, k_j=1\ldots n_j\\ \text{with}\\ \omega_j(1)=\frac{1}{\sqrt{n_j}}\\ \omega_j(k)=\sqrt{\frac{2}{n_j}} , k>1 \end{array}$

次元がn1, n2, …, npの 配列Aの正規化された多次元DCT逆変換 は以下のように計算されます

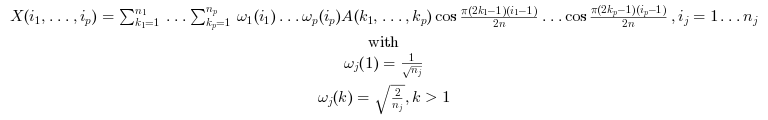
$\begin{array} \\X(i_1, \dots, i_p) = \sum_{k_1=1}^{n_1} \ldots \sum_{k_p=1}^{n_p} {\omega_1(i_1) \ldots \omega_p(i_p) A(k_1,\ldots ,k_p) \cos\frac{\pi (2 k_1 -1)(i_1-1)}{2 n} \ldots \cos\frac{\pi (2 k_p -1)(i_p-1)}{2 n}}, i_j=1\ldots n_j\\ \text{with}\\ \omega_j(1)=\frac{1}{\sqrt{n_j}}\\ \omega_j(k)=\sqrt{\frac{2}{n_j}} , k>1 \end{array}$

構文の説明

短縮構文
順方向

X=dct(A,-1 [,option]) または X=dct(A [,option]) により, オプション値を指定した順方向変換が得られます. デフォルトは,正規化された DCT-II順方向変換です.

Aがベクトルの場合 (1より大きい次元が1つだけの場合), 1次元の変換が行われ, その他の場合にはn次元変換が行われます.

(引数-1は"inverse"ではなく, 指数の符号を意味します).

逆方向

X=dct(A,1 [,option])または X=idct(A [,option])は 逆変換を行います.

Aがベクトルの場合 (1より大きい次元が1つだけの場合), 1次元の変換が行われ, その他の場合にはn次元変換が行われます.

指定した次元方向のDCTの長い構文

  • X=dct(A,sign,selection [,option]) により, 選択した次元方向のAの"スライス"の 順方向または逆方向dctを 効率的に計算することができます.

    例えば, A が3次元配列の場合, X=dct(A,-1,2) は以下と等価になります:

    for i1=1:size(A,1),
  for i3=1:size(A,3),
    X(i1,:,i3)=dct(A(i1,:,i3),-1);
  end
end

    そして X=dct(A,-1,[1 3]) は 以下と等価になります:

    for i2=1:size(A,2),
  X(:,i2,:)=dct(A(:,i2,:),-1);
end

  • X=dct(A,sign,dims,incr) は 古い構文であり,この方法でも 指定した次元方向のAのスライスの 順方向または逆方向のdctを行うことができます.

    例えば,Aが n1*n2*n3 個の要素を有する配列の場合, X=dct(A,-1,n1,1) は X=dct(matrix(A,[n1,n2,n3]),-1,1) と等価で, X=dct(A,-1,[n1 n3],[1 n1*n2]) は X=dct(matrix(A,[n1,n2,n3]),-1,[1,3]) と等価です.

dctを最適化

注意: この関数は直近のパラメータをメモリに保持し,2回目に再利用します. これにより(同じパラメータで)連続的にコールした場合の 計算時間が著しく改善されます.

get_fftw_wisdom, set_fftw_wisdom 関数により dctを更に最適化することができます.

アルゴリズム

この関数は,fftw3ライブラリを 使用します.

例

1次元dct

// 信号の周波数要素
//----------------------------------
// 50および70Hzの信号を含む1000hzで標本化された信号を構築
sample_rate=1000;
t = 0:1/sample_rate:0.6;
N = size(t,'*'); //number of samples
s = sin(2*%pi*50*t) + sin(2*%pi*70*t+%pi/4) + grand(1,N,'nor',0,1);
d = dct(s);
// 低エネルギー部分を0にする
d(abs(d)<1) = 0;
size(find(d<>0),'*') //only 30 non zero coefficients out of 600
clf;
plot(s,'b')
plot(dct(d,1),'r')

2次元 dct

function z=__milk_drop(x, y)
    sq = x.^2+y.^2;
    z = exp( exp(-sq).*(exp(cos(sq).^20)+8*sin(sq).^20+2*sin(2*(sq)).^8) );
endfunction
x = -2:0.1:2;
[X,Y] = ndgrid(x,x);
A = __milk_drop(X,Y);
d = dct(A);
d(abs(d)<1)=0;
size(find(d<>0),'*')
A1 = dct(d,1);
clf
gcf().color_map = graycolormap(128);
subplot(121), grayplot(x,x,A)
subplot(122), grayplot(x,x,A1)

参照

参考文献

Matteo Frigo and Steven G. Johnson, "FFTW Documentation" http://www.fftw.org/#documentation

Report an issue
<< Transforms Transforms dst >>
Copyright (c) 2022-2024 (Dassault Systèmes)
Copyright (c) 2017-2022 (ESI Group)
Copyright (c) 2011-2017 (Scilab Enterprises)
Copyright (c) 1989-2012 (INRIA)
Copyright (c) 1989-2007 (ENPC)
with contributors 		Last updated:
Tue Mar 07 09:28:46 CET 2023