CLSS

Représentation d'état en temps continu

Aperçu

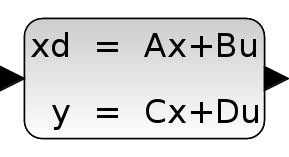
Contenu

Description

Ce bloc réalise une représentation d'état linéaire en temps continu

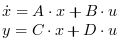
$\begin{matrix} \dot{x} = A \cdot x + B \cdot u \\ y = C \cdot x + D \cdot u \end{matrix}$

où x est le vecteur des variables d'état, u le vecteur des fonctions d'entrée et y le vecteur des variables de sortie.

Le système est défini par les matrices (A, B, C, D) et l'état initial X0. Les dimensions doivent être compatibles.

Paramètres

A matrix

La matrice carrée A.

Propriétés Type 'mat' de taille [-1,-1].
B matrix

La matrice B , [] Ssi le système n'a pas d'entrées.

Propriétés Type 'mat' de taille ["size(%1,2)","-1"].
C matrix

La matrice C, [] si le système n'a pas de sorties.

Propriétés Type 'mat' de taille ["-1","size(%1,2)"].
D matrix

La matrice D, [] si le système n'a pas de terme D.

Propriétés Type 'mat' de taille [-1,-1].
Initial state

Un vecteur/scalaire : l'état initial du système.

Propriétés Type 'vec' de taille "size(%1,2)".

Propriétés par défaut

always active: oui
direct-feedthrough: non
zero-crossing: non
mode: non
regular inputs:

- port 1 : size [1,1] / type 1
regular outputs:

- port 1 : size [1,1] / type 1
number/sizes of activation inputs: 0
number/sizes of activation outputs: 0
continuous-time state:oui
discrete-time state: non
object discrete-time state:non
name of computational function: csslti4

Fonction d'interfaçage

SCI/modules/scicos_blocks/macros/Linear/CLSS.sci

Fonction de calcul

SCI/modules/scicos_blocks/src/c/csslti4.c (Type 4)

Exemple

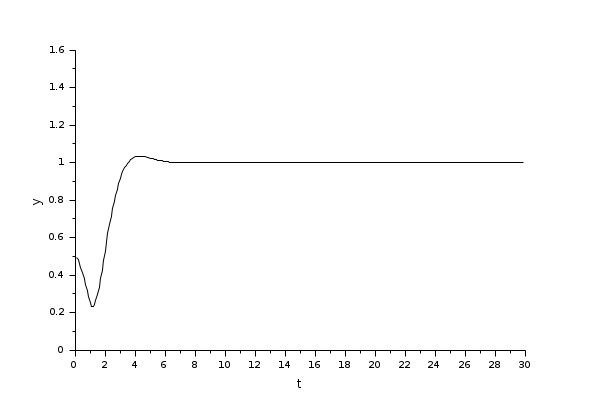
Cet exemple illustre l'utilisation du bloc CLSS pour simuler et afficher la forme d'onde en sortie y(t)=Vc(t) du circuit RLC ci-dessous.

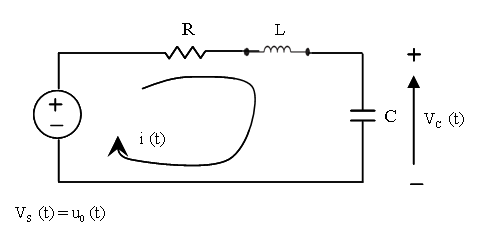
Les équations pour un circuit RLC sont les suivantes. Elles résultent des lois en tension de Kirchhoff's et de la loi de Newton.

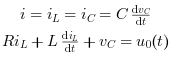
$\begin{matrix} i = i_L = i_C = C \frac{\mathrm{d} v_C }{\mathrm{d} t} \\ Ri_L + L \frac{\mathrm{d} i_L }{\mathrm{d} t} + v_C = u_0(t) \end{matrix}$

R, L et C sont les résistance, inductance et capacité du système.

Nous définissons la tension aux bornes de la capacité Vc et le courant dans l'inductance iL comme variables d'état X1 et X2.

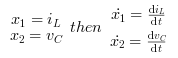
$\begin{array}{c} \mbox{$x_1 = i_L$}\\ \mbox{$x_2 = v_C$}\\ \end{array} then \begin{array}{c} \mbox{$\dot{x_1} = \frac{\mathrm{d} i_L }{\mathrm{d} t}$}\\ \mbox{$\dot{x_2} = \frac{\mathrm{d} v_C }{\mathrm{d} t}$} \end{array}$

d'où

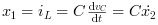
$x_1 = i_L = C\frac{\mathrm{d} v_C }{\mathrm{d} t} = C\dot{x_2}$

En réarrangeant ces équations on obtient :

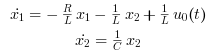
$\begin{array}{c} \dot{x_1} = -\frac{R}{L} x_1 - \frac{1}{L} x_2 + \frac{1}{L} u_0(t) \\ \dot{x_2} = \frac{1}{C} x_2 \end{array}$

Ces équations peuvent être mises sous forme d'un système matriciel comme suit ,

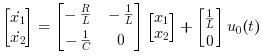
$\begin{bmatrix}\dot{x_1}\\\dot{x_2}\end{bmatrix} = \begin{bmatrix} -\frac{R}{L} & -\frac{1}{L}\\ -\frac{1}{C} & 0 \end{bmatrix} \begin{bmatrix}x_1\\x_2\end{bmatrix} + \begin{bmatrix}\frac{1}{L}\\0\end{bmatrix} u_0(t)$

L'équation de sortie requise est :

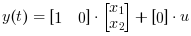
$y(t) = \begin{bmatrix} 1 & 0 \end{bmatrix} \cdot \begin{bmatrix} x_{1} \\ x_{2} \end{bmatrix} + \begin{bmatrix} 0 \end{bmatrix} \cdot u$

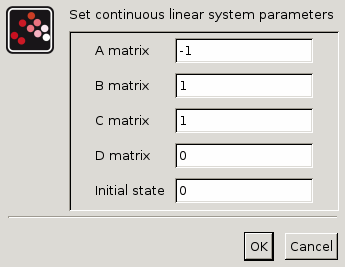
Le schéma suivant montre ces équations modéllisées dans Xcos où R= 10 Ω, L= 5 mΗ et C= 0,1 µF; Les états initiaux sont x1=0 et x2=0,5.

Pour obtenir la sortie Vc(t) on utilise le bloc CLSS de la palette Systèmes à temps continu.

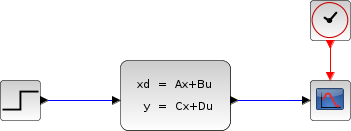
Report an issue
<< CLR	Palette Systèmes à temps continu	DERIV >>

Copyright (c) 2022-2024 (Dassault Systèmes)
Copyright (c) 2017-2022 (ESI Group)
Copyright (c) 2011-2017 (Scilab Enterprises)
Copyright (c) 1989-2012 (INRIA)
Copyright (c) 1989-2007 (ENPC)
with contributors

Last updated:
Mon Mar 27 10:12:39 GMT 2023