CLSS
連続系状態空間システム
ブロックのスクリーンショット
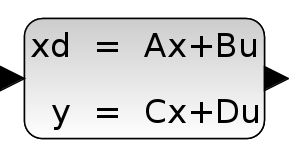
説明
このブロックは,連続時間線形状態空間システムを実現します.
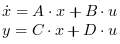
ただし,x は状態変数ベクトル, u は入力関数ベクトル, y 出力変数ベクトルです.
システムは, (A, B, C, D) 行列と状態変数初期値 X0で定義されます. 次元は互換性を有する必要があります.
ダイアログボックス
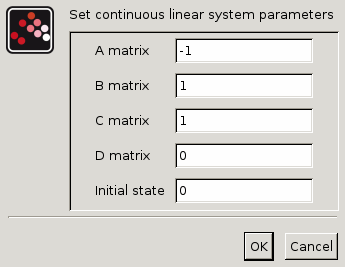
A 行列
正方行列.
プロパティ : 大きさ [-1,-1]の'mat'型.
B 行列
B 行列, システムが入力を有さない場合は [] .
プロパティ : 大きさ ["size(%1,2)","-1"] の 'mat'型.
C 行列
C 行列 , システムが入力を有さない場合は [] .
プロパティ : 大きさ ["-1","size(%1,2)"] の 'mat'型.
D 行列
D 行列, システムがD項を有さない場合は [].
プロパティ : 大きさ [-1,-1] の 'mat'型.
状態変数初期値
系のベクトル/スカラー状態変数初期値.
プロパティ : 大きさ "size(%1,2)" の 'vec'型.
デフォルトプロパティ
常にアクティブ: yes
直達項: no
ゼロ交差: no
モード: no
標準入力:
- ポート 1 : 大きさ [1,1] / 1型
標準出力:
- ポート 1 : 大きさ [1,1] / 1型
アクティベーション入力の数/大きさ: 0
アクティベーション出力の数/大きさ: 0
連続時間状態量: yes
離散時間状態量: no
オブジェクト離散時間状態量: no
計算用関数の名前: csslti4
インターフェイス用関数
SCI/modules/scicos_blocks/macros/Linear/CLSS.sci
計算用関数
SCI/modules/scicos_blocks/src/c/csslti4.c (Type 4)
例
このサンプル例は,出力波形をシミュレート/表示するための以下に示す RLC回路y(t)=Vc(t)の 出力波形をシミュレート/表示するCLSSブロックの使用法を説明します.
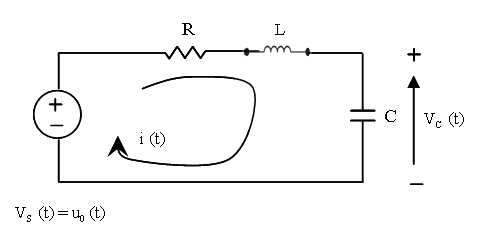
RLC回路の方程式を以下に示します. 結果はキルヒホッフの電圧則とニュートンの法則から得られます.
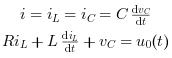
R, L および C はシステムの抵抗, インダクタンスおよびキャパシタ です.
キャパシタ電圧Vcとインダクタンス電流
iLを状態変数
X1 および X2として定義します.
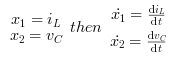
つまり
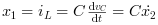
これらの方程式を整理することにより,以下を得ます:
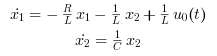
これらの方程式は 以下のような行列形式に変換できます,
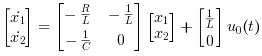
必要な出力方程式は
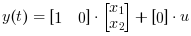
以下のダイアグラムはXcos上でモデル化されたこれらの方程式を示します. ただし, R= 10 Ω, L= 5 mΗ and C= 0.1 µF; 状態変数初期値は x1=0 および x2=0.5です.
出力 Vc(t) を得るために,連続時間システムパレットから CLSSブロックを使用します.
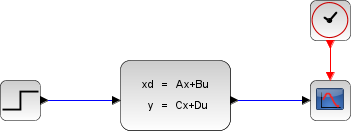
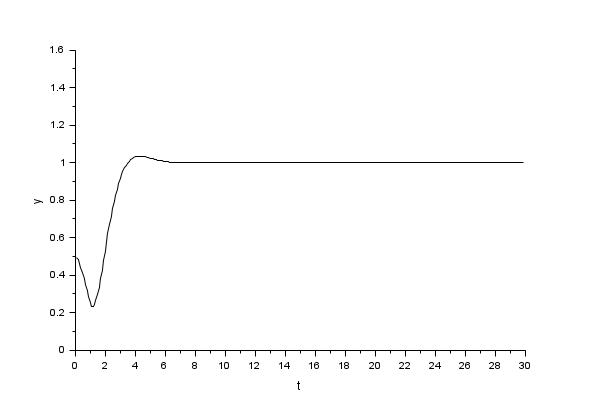
| Report an issue | ||
| << CLR | Continuous time systems palette | DERIV >> |