- Справка Scilab
- Signal Processing
- Filters
- How to design an elliptic filter
- analpf
- buttmag
- casc
- cheb1mag
- cheb2mag
- ell1mag
- eqfir
- eqiir
- faurre
- ffilt
- filt_sinc
- filter
- find_freq
- frmag
- fsfirlin
- group
- hilbert
- iir
- iirgroup
- iirlp
- kalm
- lev
- levin
- lindquist
- remez
- remezb
- sgolay
- sgolaydiff
- sgolayfilt
- srfaur
- srkf
- sskf
- syredi
- system
- trans
- wfir
- wfir_gui
- wiener
- wigner
- window
- yulewalk
- zpbutt
- zpch1
- zpch2
- zpell
Please note that the recommended version of Scilab is 2026.0.1. This page might be outdated.
See the recommended documentation of this function
wiener
Wiener estimate
Syntax
[xs,ps,xf,pf]=wiener(y,x0,p0,f,g,h,q,r)
Arguments
- f, g, h
system matrices in the interval
[t0,tf]- f
=
[f0,f1,...,ff], andfkis a nxn matrix- g
=
[g0,g1,...,gf], andgkis a nxn matrix- h
=
[h0,h1,...,hf], andhkis a mxn matrix
- q, r
covariance matrices of dynamics and observation noise
- q
=
[q0,q1,...,qf], andqkis a nxn matrix- r
=
[r0,r1,...,rf], andgkis a mxm matrix
- x0, p0
initial state estimate and error variance
- y
observations in the interval
[t0,tf].y=[y0,y1,...,yf], andykis a column m-vector- xs
Smoothed state estimate
xs= [xs0,xs1,...,xsf], andxskis a column n-vector- ps
Error covariance of smoothed estimate
ps=[p0,p1,...,pf], andpkis a nxn matrix- xf
Filtered state estimate
xf= [xf0,xf1,...,xff], andxfkis a column n-vector- pf
Error covariance of filtered estimate
pf=[p0,p1,...,pf], andpkis a nxn matrix
Description
function which gives the Wiener estimate using the forward-backward Kalman filter formulation
Sample
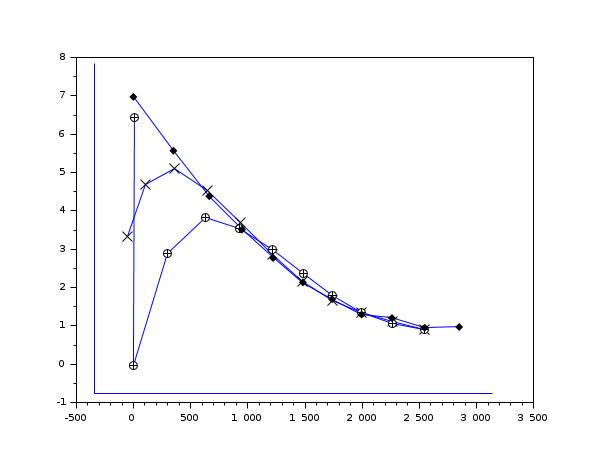
Examples
// initialize state statistics (mean and er. variance) m0=[10 10]'; p0=[100 0;0 100]; // create system f2=[1.1 50.1;0 0.8]; g=[1 0;0 1]; h=[1 0;0 1]; [hi,hj]=size(h); // noise statistics q=[.01 0;0 0.01]; r=20*eye(2,2); // initialize system process rand("seed",66); rand("normal"); p0c=chol(p0); x0=m0+p0c'*rand(ones(m0)); y=h*x0+chol(r)'*rand(ones(1:hi))'; yt=y; // initialize plotted variables x=x0; // loop ft=[f2]; gt=[g]; ht=[h]; qt=[q]; rt=[r]; n=10; for k=1:n // generate the state and observation // at time k (i.e. xk and yk) [x1,y]=system(x0,f2,g,h,q,r); x=[x x1]; yt=[yt y]; x0=x1; ft=[ft f2]; gt=[gt g]; ht=[ht h]; qt=[qt q]; rt=[rt r]; end // get the wiener filter estimate [xs,ps,xf,pf]=wiener(yt,m0,p0,ft,gt,ht,qt,rt); // plot result a=min([x(1,:)-2*sqrt(ps(1,1:2:2*(n+1))),xf(1,:),xs(1,:)]); b=max([x(1,:)+2*sqrt(ps(1,1:2:2*(n+1))),xf(1,:),xs(1,:)]); c=min([x(2,:)-2*sqrt(ps(2,2:2:2*(n+1))),xf(2,:),xs(2,:)]); d=max([x(2,:)+2*sqrt(ps(2,2:2:2*(n+1))),xf(2,:),xs(2,:)]); xmargin=max([abs(a),abs(b)]); ymargin=max([abs(c),abs(d)]); a=-0.1*xmargin+a; b=.1*xmargin+b; c=-0.1*ymargin+c; d=.1*ymargin+d; // plot frame, real state (x), and estimates (xf, and xs) scf(); plot([a a b],[d c c]); plot2d(x(1,:)',x(2,:)',[2],"000") plot2d(xf(1,:)',xf(2,:)',[2],"000") plot2d(xs(1,:)',xs(2,:)',[2],"000") // mark data points (* for real data, o for estimates) plot2d(xs(1,:)',xs(2,:)',[-2],"000") plot2d(xf(1,:)',xf(2,:)',[-3],"000") plot2d(x(1,:)',x(2,:)',[-4],"000")
| Report an issue | ||
| << wfir_gui | Filters | wigner >> |