Please note that the recommended version of Scilab is 2026.0.0. This page might be outdated.
See the recommended documentation of this function
histc
computes the histogram of a simple series of data
Syntax
Heights = histc(Data) Heights = histc(Data, nbins) Heights = histc(Data, -binsWidth) Heights = histc(Data, binsAlgo) Heights = histc(Data, binsEdges) Heights = histc(Data, binsValues [, "discrete"]) Heights = histc(Data, , Options) Heights = histc(Data, .. , Options) [Heights, jokers] = histc(Data, ..) [Heights, jokers, bins] = histc(Data, ..) [Heights, jokers, bins, inBin] = histc(Data, ..)
Arguments
Input arguments
- Data
vector, matrix or hypermatrix of encoded integers, decimal numbers, complex numbers, polynomials, or texts. Sparse-encoded matrices are accepted.
Datamust have at least 2 components.histc([],..)returns[]for every output argument.- Numerical
Datamay includeInfinite orNaNvalues. However,NaNvalues are never binned in the histogram;Infinite values can be binned only in categorial histograms. - Textual
Datamay include empty texts""or extended-ascii or UTF-8 characters.
- Binning:
histcallows to define the set of histogram bins in several ways depending on theDatatype and on the need. Two major binning types / histogram modes can be used:continuous contiguous ranging bins :this is meaningful whether
Datavalues are sortable. This is the case for encoded integers, decimal numbers, and texts.
histc()continuously bins complex numbers considering only their real parts.- Any number with either a real or imaginary part set to
%nan,-%inf, or to+%infis excluded from bins and from the histogram. - For sparse-encoded
Data, the zero value is not taken into account to define the whole binning range.
In this case, bins are defined by their edges. For a given bin, any data value being between the bin's edges belongs to it.
discrete / categorial binning mode :this can be used for any
Datatype. It is the only binning mode available for polynomial data.A categorial bin -- aka category -- is defined by its value: any data belongs to the bin if its value is equal to the bin's value.
 Any
AnyDataor bin's value beingNaNis canceled before computing the categorial histogram.
- (default)
When no binning specification is provided,
- For integers, decimal, or complex numbers, the
"sqrt"binning algorithm is used See here-below for more informations. - For texts and polynomials: the histogram is
computed in
"discrete"mode, with as many bins as there are distinct data entries.
- For integers, decimal, or complex numbers, the
- nbins
single positive integer: required number of contiguous bins of equal widths covering the whole range of non-infinite
Datavalues. This binning specification can't be used for texts
This binning specification can't be used for textsData- binsWidth
Single decimal number > 0 specifying the bins width for all bins. Its opposite
-binsWidth < 0must be provided in input (to not get confused withnbinsthat is already a single positive number).- binsAlgo
Single text word among the ones described here-below. These automatic binning modes can be used for encoded integers, decimal, or complex numbers. None of them can be used for texts or polynomial data.
For these 3 modes, the whole range of data values is shared into nB bins of equal widths. nB is set according to the chosen algorithm as follows.
"sqrt": nB is set to the square-root of the number
Nvalidof valid data inData, in such a way that there are as many bins as the average number of counts in bins. The vertical average relative resolution1 count / nB counts = 1/nBof the histogram is then similar to the horizontal onebinWidth/range = (range/nB)/range = 1/nBHowever, for encoded integers data, if the data range
dR=max(Data)-min(Data)+1is narrower than nB, nB is then set to dR, so setting the bins width to 1. Bins are then automatically centered on integer values in the range."freediac": Freedmann - Diaconis binning criterion: nB = round(strange(Data)/binWidth)withbinsWidth = 2*iqr(Data)* Nvalid^(-1/3)."sturges": Sturges binning criterion: nB = ceil(1 + log2(Nvalid))- binsEdges
Vector of values sorted in strict increasing order (without duplicates). N bins edges define N-1 bins. For encoded integers
Data,binsEdgescan be decimal numbers. For complex numbersData, decimal numbers are expected inbinsEdges: only the distribution of real parts is considered.- First bin: Any non-infinite
Datacomponent belonging to the closed interval[binsEdges(1), binsEdges(2)]belongs to the first bin and is accounted in theHeights(1)count. - Next bins # i>1: Any non-infinite
Datacomponent belonging to the semi-open interval]binsEdges(i), binsEdges(i+1)]belongs to the bin #i and is accounted in theHeights(i)count.
Marginal bins:
For numerical and text
Data, the first or/and the lastbinsEdgescomponents may be set to collect and count in marginal bins all non-infiniteDatacomponents remaining in the left and right wings of the complete histogram:- Left wing: set
binsEdges(1) = -%inf, orbinsEdges(1) = ""
Dataentries such thatData < binsEdges(2)are counted inHeights(1).- The actual
bins(1)edge is set tomin(Data).
-
Right wing: set
binsEdges($) = %inf, orbinsEdges($) = "~~"(for texts in standard ascii,ascii(126)=="~"is the last printable character)
Dataentries such thatData > binsEdges($-1)are counted inHeights($).- The actual
bins($)edge is set tomax(Data).
- First bin: Any non-infinite
- binsValues
For polynomial
Dataor when the"discrete"option is used,binsValuesprovides values whose occurrences inDatamust be counted.- Duplicates and
%nanvalues are priorly removed frombinsValues. binsValuesmay include some%infvalues. However, for encoded integersData, any%infvalue is removed before processing.- Components of
binsValuesmay be unsorted: the order ofbinsValuescomponents is kept as is in theHeightsoutput vector.
- Duplicates and
- Options
Optionsis either a vector of textual flags, or equivalently a single word of comma-separated concatenated flags, or both. All flags are case-insensitive and can be specified in any order.Examples: The following options specifications are equivalent:
["discrete" "countsNorm" "normWith: Out Inf"], or["countsNORM" "NORMwith: inf out" "Discrete" ], or["normWith: INF OUT", "discrete, countsNorm" ], or simply"discrete,countsNorm,normWith: inf out".- "discrete"
This flag must be used when a discrete / categorial histogram is required. Then, the vector provided in argument #2 with at least 2 components sets bins values instead of bins edges (by default).
 Presently, polynomial
Presently, polynomialDataare always processed in a categorial way. The"discrete"flag looks then useless. However, in a future release, polynomials could become sortable. Using the"discrete"flag does not hurt and would avoid future back-compatibility issues.- Histogram scale:
"counts" This mode is the default one: Whatever is each bin's width, the height of the bin is equal to the number of
Datacomponents falling in it."countsNorm" Whatever is each bin's width and position, the height of the bin is equal to the relative number of
Datacomponents falling in it, over all counted components. Then, unless the"normWith:.."option is used, the cumulated bins heights is equal to 1:sum(Heights)==1."density" The area of each bin is equal to the number of
Datacomponents falling in it. This scaling mode is meaningless and ignored in case of categorial histogram."densityNorm" The area of each bin is equal to the relative number of
Datacomponents falling in it. Then, unless the"normWith:.."option is used, the whole area of the histogram is equal to 1: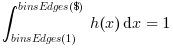
This scaling mode is meaningless and ignored in case of categorial histogram.
- "normWith:.."
When the
"countsNorm"or"densityNorm"option is used, it is possible to provide additional informations about which components ofDataout of bins should be considered for the total number N of counts over which the normalization is computed.After the
"normWith:"option's header, a space-separated list of case-insensitive flags can be provided in any order. If several concurrent flags are provided, only the last specified one is taken into account. Unrelevant flags for the givenDatatype are ignored. Available flags and their relative priorities are described here-below. Examples:"normWith: all","normWith: out inf","normWith: Nan inf","normWith: rightout inf", etc."all" All components of Dataare considered:N = size(Data,"*"). If"all"is used, all other"normWith:.."options are ignored."out" All Dataout ofbinsthat are notNanorInfor""are accounted. IfDatais sparse-encoded, zeros remain excluded unless the option"normWith: zeros"is used. If"out"is used,"leftout"and"rightout"options are ignored."leftout" As with "out", but only forData < binsEdges(1). This flag is ignored in discrete/categorial mode."rightout" As with "out", but only forData > binsEdges($). This flag is ignored in discrete/categorial mode."NaN" NaNdata are accounted, in addition to other ones."Inf" Infdata are accounted, in addition to other ones.In discrete/categorial mode,
Infvalues are not specific and are processed as other ones. This flag is then ignored."zeros" If Datais sparse-encoded, by default only non-zero elements are considered (otherwise, zeros are not specific and are processed as other values). Nevertheless, it's possible to take them into account in the normalization by using this"normWith: zeros"flag. Using this flag does not credit the
Using this flag does not credit theHeightsof the bin covering the zero value (if any)."empty" ""empty texts inDataare accounted, in addition to other ones.
Results
- Heights
vector of decimal numbers whose values depend on the histogram scaling mode set with each dedicated option. See the description of the
Histogram scalesoptions here-above. In brief:"counts"mode:Heights(i)is the number ofDatacomponents equal to thebins(i)value (categorial), or belonging to the]bins(i), bins(i+1)]interval (continuous histogram)."countsNorm"mode:Heights(i)is as for"counts", divided by the total numberNof consideredDatacomponents.Nis the sum of counts in all bins, plus possibly the number of counts of some special jokers values (%inf, %nan, 0, ""), according to thenormWith:option used.
In continuous mode, statistical densities may be returned in the vector
Heightsinstead of integer numbers of counts: Let's callcounts(i)the number of counts in the bin #i defined by its edges. Then- In
"density"mode:Heights(i)is set such that the area of the bin is equal to its population:Heights(i) * (binsEdges(i+1) - binsEdges(i)) == counts(i). - In
"densityNorm"mode: the"density"results are divided by the total numberNof considered counts (see"countsNorm").
- jokers
Row vector of 1 to 5 decimal numbers indicating the frequency of special values in
Data. Let's define the following numbers:Nnan: number ofNaNobjects inData.Ninf: number ofInfobjects inData.Nzeros: number of null values inData.Nempty: number of empty texts "" inData.Nleftout: number ofDatacomponents not equal to-%infnor to"", such thatData < binsEdges(1).Nrightout: number ofDatacomponents not equal to%infsuch thatData > binsEdges($).Nout: number ofDatacomponents out of bins, non-infinite, not beingNan, not being empty text"", and for sparseData: not equal to zero.
In unnormalized
"counts"and"density"histogram scales,jokersreturns the integer counts numbers of special values.In normalized
"countsNorm"and"densityNorm"histogram scales,jokersreturns countsNorm frequencies of special values.Then, according to the
Datatype and the continuous or categorial histogram mode,jokersis made of the following:- Encoded integers:
- continuous:
[Nleftout, Nrightout] - categorial:
[Nout]
- continuous:
- Decimal or complex numbers, full or sparse:
- continuous:
[Nleftout, Nrightout, Nzeros, Nnan, Ninf] - categorial:
[Nout, 0, Nzeros, Nnan, Ninf]
- continuous:
- Polynomials:
[Nout, 0, 0, Nnan, Ninf] - Texts:
- continuous:
[Nleftout, Nrightout, Nempty] - categorial:
[Nout, 0, Nempty]
- continuous:
- bins
Row vector of bins edges or of bins values actually used to build the histogram.
histc()allows using many semi-automatic or automatic binning modes for which no explicit or incompletebinsEdgesorbinsValuesvector is provided as input.- Continuous binning mode:
- The actual
binsEdgesis returned inbins. It has theHeightsnumber of components, + 1 (position of the closing edge). For encoded integers, decimal numbers, and complex numbers
Data,binsis of decimal type. For textData,binsis of type text as well.When marginal bins are required (see the
binsEdgesdescription)bins(1)andbins($)return the actual boundaries of the whole binning range used.
- The actual
- Discrete categorial mode:
For polynomial
Data, or for otherDatatypes used with the"discrete"option: if no explicitbinsValuesvector is provided,histc()sets it tounique(Data)(:)'and returns it asbins.
- Continuous binning mode:
- inBin
Array of decimal integers having the sizes of
Data. IfDatais sparse-encoded,inBinis so as well.inBin(i,j)returns the index of thebinswhichData(i,j)belongs to. If the value ofData(i,j)is out of bins,inBin(i,j)=0. Otherwise,Data(i,j)increments theHeights(inBin(i,j))counts by one unit.
Examples
with decimal numbers:
data = [1 1 1 2 2 3 4 4 5 5 5 6 6 7 8 8 9 9 9]; N = size(data,"*") // ==19 // Default binning; "sqrt": sqrt(19) => 4. .. => 4 bins [h, j, b, i] = histc(data) // expected: h = [6 5 3 5] = href // expected: b = [1 3 5 7 9] bins edges // expected: i = [1 1 1 1 1 1 2 2 2 2 2 3 3 3 4 4 4 4 4] d memberships to bins histc(data, , "countsNorm") // Expected: href/N histc(data, , "density") // Expected: href/2, 2 being the bins width histc(data, , "densityNorm") // Expected: href/N/2 // Automatic Sturges binning [h, j, b, i] = histc(data,"sturges") // h = [5 1 5 2 1 5] // b = [3 7 11 15 19 23 27] / 3 // i = [1 1 1 1 1 2 3 3 3 3 3 4 4 5 6 6 6 6 6] // Explicit bins edges, with marginal bins // --------------------------------------- data = [1 1 1 2 2 3 4 4 5 5 5 6 6 7 8 8 9 9 9]; be = [-%inf 3 5 7 %inf]; [href, j, b, i] = histc(data, be) // href = [6 5 3 5] => sum N = 19 // b = [1 3 5 7 9] // bins completed with actual data bounds // i = [1 1 1 1 1 1 2 2 2 2 2 3 3 3 4 4 4 4 4] histc(data, be, "countsNorm") // href/N histc(data, be, "density") // href/2 bins width = 2: see b histc(data, be, "densityNorm") // href/N/2 // Explicit bins edges, with outsiders // ----------------------------------- data = [1 1 1 2 2 3 4 4 5 5 5 6 6 7 8 8 9 9 9]; // still the same be = [2, 5.5, 7]; // Bins edges (2 bins) [href, jref, b, i] = histc(d, be) // href = [8 3] jref = [3 5 0 0 0] = [leftout, rightout, ..] // i = [0 0 0 1 1 1 1 1 1 1 1 2 2 2 0 0 0 0 0] histc(data, be, "countsNorm") // href / 11 histc(data, be, "countsNorm, normWith: leftout") // href / 14 histc(data, be, "countsNorm, normWith: rightout") // href / 16 histc(data, be, "countsNorm, normWith: out") // href / 19 histc(data, be, "density") // href ./ diff(be) histc(data, be, "densityNorm") // href ./ diff(be) / 11 histc(data, be, "densityNorm, normWith: leftout") // href ./ diff(be) / 14 histc(data, be, "densityNorm, normWith: rightout") // href ./ diff(be) / 16 histc(data, be, "densityNorm, normWith: all"); // href ./ diff(be) / 19 // With Nan and Inf values // ----------------------- data = [1 1 1 2 2 3 4 4 5 5 5 6 6 7 8 8 9 9 9]; data = [%nan %inf, data, %nan %nan -%inf]; N = size(data,"*"); // 24 be = [2, 4.5, 7]; // Set bins edges (2 bins) [href, jref, b, iref] = histc(data, be) // href = [5 6] jref = [3 5 0 3 2]; // continuous mode: jokers = [leftout, rightout, zeros, nan, inf] // iref = [0 0 0 0 0 1 1 1 1 1 2 2 2 2 2 2 0 0 0 0 0 0 0 0] memberships [h, j] = histc(data, be, "countsNorm") // Expected: href/11, jref/11 [h, j] = histc(data, be, "countsNorm, normWith: nan") // Expected: href/14, jref/14 [h, j] = histc(data, be, "countsNorm, normWith: inf") // Expected: href/13, jref/13 [h, j] = histc(data, be, "countsNorm, normWith: inf nan") // Expected: href/16, jref/16 [h, j] = histc(data, be, "countsNorm, normWith: leftout nan") // Expected: href/17, jref/17 [h, j] = histc(data, be, "countsNorm, normWith: rightout inf") // Expected: href/18, jref/18 [h, j] = histc(data, be, "countsNorm, normWith: out inf") // Expected: href/21, jref/21 [h, j] = histc(data, be, "countsNorm, normWith: all") // Expected: href/24, jref/24 // Normalized densities over a Bins width = 2.5 (see be) [h, j] = histc(data, be, "densityNorm") // Expected: href/11/2.5, jref/11 [h, j] = histc(data, be, "densityNorm, normWith: nan") // Expected: href/14/2.5, jref/14 [h, j] = histc(data, be, "densityNorm, normWith: inf") // Expected: href/13/2.5, jref/13 [h, j] = histc(data, be, "densityNorm, normWith: inf nan") // Expected: href/16/2.5, jref/16 [h, j] = histc(data, be, "densityNorm, normWith: leftout nan") // Expected: href/17/2.5, jref/17 [h, j] = histc(data, be, "densityNorm, normWith: rightout inf") // Expected: href/18/2.5, jref/18 [h, j] = histc(data, be, "densityNorm, normWith: all") // Expected: href/24/2.5, jref/24
with texts:
histc(["a" "c" "a" "a" "b" "c"]) // [3 1 2] t = [ "c" "n" "h" "i" "b" "i" "f" "i" "p" "l" "p" "d" "f" "i" "l" "b" "m" "e" "o" "o" "f" "p" "o" "h" "f" "h" "h" "c" "k" "o" "p" "f" "k" "a" "j" "o" "j" "d" "h" "h" "n" "m" "o" "l" "n" "h" "b" "o" "l" "j" "n" "o" "i" "g" "i" "a" "a" "j" "d" "p" ]; // With default discrete bins // -------------------------- [h,j,b,i] = histc(t) // h = [3 3 2 3 1 5 1 7 6 4 2 4 2 4 8 5] // b = "a" b c d e f g h i j k l m n o p iref = [ 3 14 8 9 2 9 6 9 16 12 16 4 6 9 12 2 13 5 15 15 6 16 15 8 6 8 8 3 11 15 16 6 11 1 10 15 10 4 8 8 14 13 15 12 14 8 2 15 12 10 14 15 9 7 9 1 1 10 4 16 ]; // With given discrete bins WITHOUT "" bins // ---------------------------------------- t2 = t; t2([7 13 19 26 32 39 43]) = ""; // --> t2 = // c n h b i f i p l p d f i l // b m e o o f o h f h h c k o // p k a o j d h m o l n // h b o l j n o g i a a j d p // // b = '' a b c d e f g h i j k l m n o p // h = 7 3 3 2 3 1 4 1 6 4 3 2 4 2 3 8 4 [h, j, b, i] = histc(t2, ["a" "e" "i" "o"], "discrete") // h = [3 1 4 8]; N = 16 // j = [37 0 7] = [out, 0, #""] // i = [ // memberships // 0 0 0 0 0 3 0 3 0 0 0 0 0 3 0 // 0 0 2 4 4 0 0 4 0 0 0 0 0 0 4 // 0 0 0 1 0 4 0 0 0 0 0 0 4 0 0 // 0 0 4 0 0 0 4 0 0 3 1 1 0 0 0 // ]; // With continuous and marginal bins: "" <=> -inf , "~~" <=> Inf (regular ascii) // ----------------------------------------------------------------------------- [h,j,b,i] = histc(t, ["" "c" "e" "g" "i" "k" "m" "~~"]) // h = [8 4 6 13 6 6 17] j = [0 0 0] // i = [ // memberships // 1 7 4 4 1 4 3 4 7 6 7 2 3 4 6 // 1 6 2 7 7 3 7 7 4 3 4 4 1 5 7 // 7 3 5 1 5 7 5 2 4 4 7 6 7 6 7 // 4 1 7 6 5 7 7 4 3 4 1 1 5 2 7 // ]; // Continuous bins. Data WITH "" // ----------------------------- // t2 = // c n h b i f i p l p d f i l // b m e o o f o h f h h c k o // p k a o j d h m o l n // h b o l j n o g i a a j d p // // b = '' a b c d e f g h i j k l m n o p // h = 7 3 3 2 3 1 4 1 6 4 3 2 4 2 3 8 4 binsEdges = ["e" "f" "g" "h" "i" "j"]; [href, jref, b, i] = histc(t2, binsEdges) // href=[5 1 6 4 3]; N = sum(href) = 19 // jref=[11 23 7]; [leftout rightout ""] [h,j,b,i] = histc(t2, binsEdges, "countsNorm,normWith: leftout") // h = href / (N+jref(1)), j = jref / (N+jref(1)) [h,j,b,i] = histc(t2, binsEdges, "countsNorm,normWith: rightout") // h = href / (N+jref(2)), j = jref / (N+jref(2)) [h,j,b,i] = histc(t2, binsEdges, "countsNorm,normWith: out"); // h = href / sum([N jref(1:2)]), j = jref / sum([N jref(1:2)]) [h,j,b,i] = histc(t2, binsEdges, "countsNorm,normWith: empty") // h = href / (N+jref(3)), j = jref/(N+jref(3)) [h,j,b,i] = histc(t2, binsEdges,"countsNorm,normWith: out empty") // h = href / sum([N jref]), j = jref / sum([N jref]) [h,j,b,i] = histc(t2, binsEdges, "countsNorm,normWith: all") // h = href / sum([N jref]), j = jref/sum([N jref])
with polynomials:
histc([%z 2+%z %z]) // [2 1] histc([%z 2+%z %z],, "countsnorm") // [2 1] / 3 histc([%z 2+%z %z %nan],, "countsnorm") // [2 1] / 3 histc([%z 2+%z %z %nan],, "countsnorm, normWith: Nan") // [2 1] / 4 // Data order is kept: histc([2+%z %z %z ]) == [1 2]
See also
- histplot — plot a histogram
- bar3d — 3D гистограмма
- bar — bar histogram
- barh — horizontal display of bar histogram
- plot2d2 — 2D plot (step function)
- dsearch — поиск в упорядоченных наборах
- members — count (and locate) in an array each element or row or column of another array
- grep — поиск соответствий строки в векторе строк
- strcmp — сравнение символьных строк
- isnan — проверка на нечисловые элементы ("Nan")
- isinf — проверка на бесконечные элементы
History
| Версия | Описание |
| 5.5.0 | histc() introduced |
| 6.1.0 | histc() reforged:
|
| Report an issue | ||
| << cmoment | Empirical distribution | moment >> |