number_properties

determina parâmetros de ponto flutuante

Seqüência de Chamamento

pr = number_properties(prop)

Parâmetros

prop: string
pr: escalar real ou booleano

Descrição

Esta função pode ser usada para receber os números/propriedades característicos do conjunto de pontos flutuantes aqui dentoado por F(b,p,emin,emax) ((geralmente o conjunto de "floats" de 64 bits prescritos por IEEE 754). Números de F são da forma:

sign * m * b^e

e é o expoente e m a mantissa:

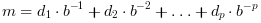
$m = d_1 \cdot b^{-1} + d_2 \cdot b^{-2} + \ldots + d_p \cdot b^{-p}$

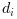$d_i$ os dígitos estão em [0, b-1] ee em [emin, emax], o número é dito "normalizado" se 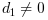$d_1 \neq 0$ . Os seguintes podem ser recebidos:

prop = "radix": então pr é a raiz b do conjunto F
prop = "digits": então pr é o número de dígitos de p
prop = "huge": então pr é o maior float positivo de F
prop = "tiny": então pr é o menor float normalizado positivo de F
prop = "denorm": então pr é um booleano (%t se números denormalizados são utilizados)
prop = "tiniest": então se denorm = %t, pr é o número positivo denormalizado mínimo. Em outro caso, pr = tiny
prop = "eps": então pr é a máquina epsilon ( geralmente (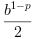 $\dfrac{b^{1-p}}{2}$ ) que é o erro máximo relativo entre um real x (tal que |x| está em [tiny, huge]) e fl(x), sua aproximação em ponto flutuante em F
prop = "minexp": então pr é emin
prop = "maxexp": então pr é emax

Esta função usa uma rotina de LAPACK dlamch para receber os parâmetros máquinas (os nomes (radix, digits, huge, etc...) são aqueles recomendados pelo padrão LIA 1 e são diferentes daqueles correspondentes em LAPACK).

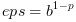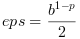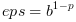Às vezes você poderá encontrar a seguinte para a máquina epsilon: $eps = b^{1-p}$ , mas nesta função nós usamos a definição tradicional (ver prop = "eps" acima) e então $eps = \dfrac{b^{1-p}}{2}$ se o arredondamento normal acontecer e $eps = b^{1-p}$ se não acontecer.

Exemplos

b = number_properties("radix")
eps = number_properties("eps")

Ver Também

nearfloat — get previous or next floating-point number
log2 — Base-2 logarithm. Base-2 exponent and mantissa of some real numbers
-0 — Processing of -0 versus 0

Report an issue
<< nextpow2	Ponto flutuante	round >>

Copyright (c) 2022-2024 (Dassault Systèmes)
Copyright (c) 2017-2022 (ESI Group)
Copyright (c) 2011-2017 (Scilab Enterprises)
Copyright (c) 1989-2012 (INRIA)
Copyright (c) 1989-2007 (ENPC)
with contributors

Last updated:
Mon Jan 03 14:35:22 CET 2022