Please note that the recommended version of Scilab is 2026.0.1. This page might be outdated.
See the recommended documentation of this function
bsplin3val
função de avaliação de derivada arbitrária de spline 3d
Seqüência de Chamamento
dfp = bsplin3val(xp, yp, zp, tl, der)
Parâmetros
- xp, yp, zp
vetores ou matrizes de reais de tamanhos iguais
- tl
tlist de tipo "splin3d", definindo um tensor spline 3d (chamado de
sa seguir)- der
vetor com três componentes
[ox,oy,oz]definindo qual derivada descomputar.- dfp
vetor ou matriz de mesmo formato que
xp,ypezp, avaliação elemento a elemento da derivada especificada desnesses pontos.
Descrição
Enquanto a função interp3d pode
computar apenas o spline s e suas primeiras derivadas,
bsplin3val pode computar qualquer derivada de
s. A derivada a ser computada é especificada pelo
argumento der=[ox,oy,oz] :
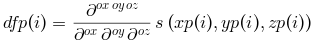
Então, der=[0 0 0] corresponde a
s, der=[1 0 0] to
ds/dx, der=[0 1 0] to
ds/dy, der=[1 1 0] to
d2s/dxdy, etc...
Para um ponto com coordenadas (xp(i),yp(i),zp(i)) fora do grid, a função retorna 0.
Exemplos
deff("v=f(x,y,z)","v=cos(x).*sin(y).*cos(z)"); deff("v=fx(x,y,z)","v=-sin(x).*sin(y).*cos(z)"); deff("v=fxy(x,y,z)","v=-sin(x).*cos(y).*cos(z)"); deff("v=fxyz(x,y,z)","v=sin(x).*cos(y).*sin(z)"); deff("v=fxxyz(x,y,z)","v=cos(x).*cos(y).*sin(z)"); n = 20; // n x n x n pontos de interpolação x = linspace(0,2*%pi,n); y=x; z=x; // grid de interpolação [X,Y,Z] = ndgrid(x,y,z); V = f(X,Y,Z); tl = splin3d(x,y,z,V,[5 5 5]); // computando f e algumas derivadas em um ponto // e comparando com o spline interpolante xp = grand(1,1,"unf",0,2*%pi); yp = grand(1,1,"unf",0,2*%pi); zp = grand(1,1,"unf",0,2*%pi); f_e = f(xp,yp,zp) f_i = bsplin3val(xp,yp,zp,tl,[0 0 0]) fx_e = fx(xp,yp,zp) fx_i = bsplin3val(xp,yp,zp,tl,[1 0 0]) fxy_e = fxy(xp,yp,zp) fxy_i = bsplin3val(xp,yp,zp,tl,[1 1 0]) fxyz_e = fxyz(xp,yp,zp) fxyz_i = bsplin3val(xp,yp,zp,tl,[1 1 1]) fxxyz_e = fxxyz(xp,yp,zp) fxxyz_i = bsplin3val(xp,yp,zp,tl,[2 1 1])
| Report an issue | ||
| << Interpolação | Interpolação | cshep2d >> |