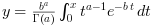gamma

Arguments

u

array of positive or negative real numbers

gamma(u) and gamma(x,…) can be overloaded for complex numbers with %s_gamma_user(), and for other a types with the usual overload naming rule.

x, a, b

arrays of positive real numbers. If at least one input is not scalar, scalar ones are expanded to its size. If several inputs are not scalar, they must have the same size.

y

array of real numbers, with the size of u or of (the non-scalar) x, a, or b.

Description

gamma(…) computes and yields the complete or incomplete gamma function for each element of its input(s), in an element-wise way. The complete gamma function extends the factorial one to non-integer real positive or negative numbers, as gamma(u+1)=u*gamma(u).

gamma(u) computes

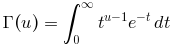
Incomplete normalized integrals

gamma(x, a) computes the integral

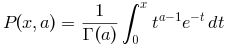
gamma(x, a, b) computes the generalized integral

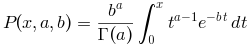
gamma(x, a, "upper") computes accurately the complementary integral 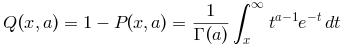even for big x and P(x,a)→1. Finally,

gamma(x, a, b, "upper") computes the generalized complementary integral

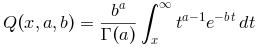
The inverse incomplete normalized gamma function can be computed with x = cdfgam("X", a, b, y, 1-y), that is the x bound such that Calling x = cdfgam("X", a, b, z-1, z) with z=1-y will be preferred when 0.5 < y < 1, to get a full accuracy on x.

Examples

Gamma as the extension of the factorial function to non-integer numbers:

[gamma(2:7) ; factorial(1:6)]
gamma(1.5:7)
gamma(1.5:7) ./ gamma(0.5:6)

--> [gamma(2:7) ; factorial(1:6)]
 ans  =
   1.   2.   6.   24.   120.   720.
   1.   2.   6.   24.   120.   720.

--> gamma(1.5:7)
 ans  =
   0.8862269   1.3293404   3.323351   11.631728   52.342778   287.88528

--> gamma(1.5:7) ./ gamma(0.5:6)
 ans  =
   0.5   1.5   2.5   3.5   4.5   5.5

Graph of the Gamma function around 0:

[a, b] = (-3, 5);
x = linspace(a,b,40000);
y = gamma(x);
clf
plot2d(x, y, style=0, axesflag=5, rect=[a,-10,b,10])
title("$\Gamma(u)$", "fontsize",3.5)
xgrid(color("grey60"))

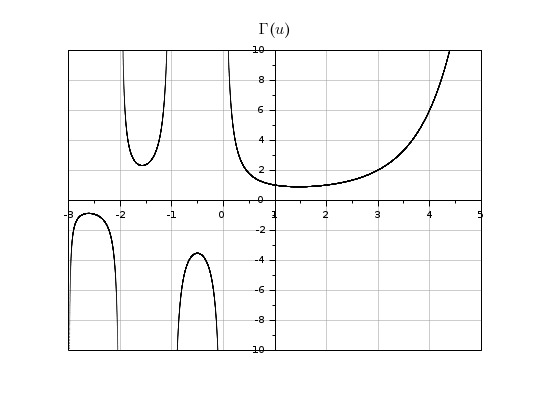
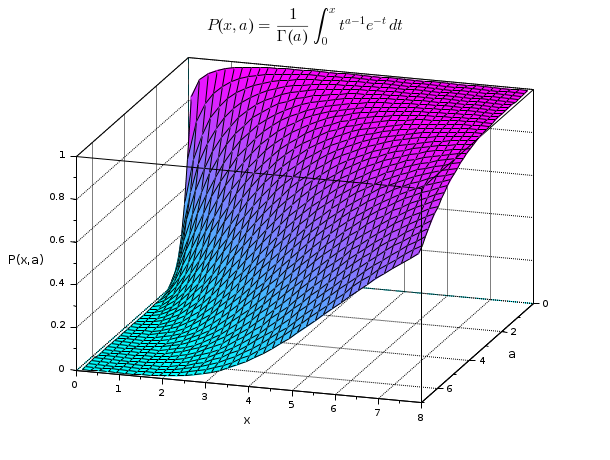
Incomplete normalized P(x,a) gamma function:

x = 0.1:0.2:8;
a = 0.1:0.2:7;
[X, A] = ndgrid(x, a);
P = gamma(X,A);
clf
gcf().color_map = coolcolormap(100);
surf(a,x,P)
title("$P(x,a)=\frac{1}{\Gamma(a)}\int_0^x\! t^{a-1}e^{-t}\,dt$","fontsize",3.5)
xlabel(["" "a"], "fontsize",2)
ylabel("x", "fontsize",2)
zlabel("P(x,a)", "fontsize",2)
xgrid

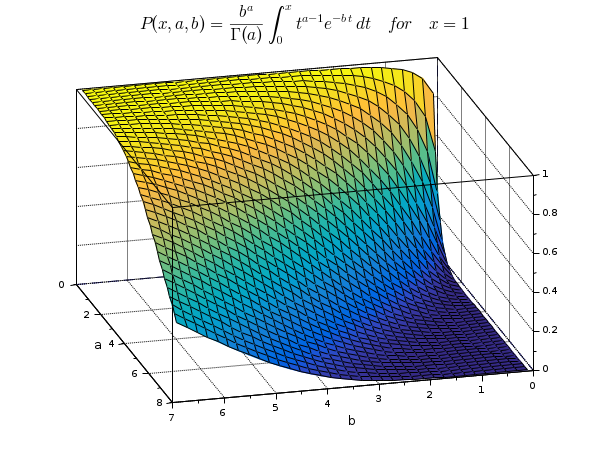
Incomplete generalized normalized P(x,a,b) function:

a = 0.1:0.2:8;
b = 0.1:0.2:7;
[A, B] = ndgrid(a, b);
P = gamma(1,A,B);
clf
gcf().color_map = parulacolormap(100);
surf(b,a,P)
title("$P(x,a,b)=\frac{b^a}{\Gamma(a)}\int_0^x\! t^{a-1}e^{-b\,t}\,dt\quad for\quad x=1$","fontsize",3.7)
xlabel("b", "fontsize",2)
ylabel("a", "fontsize",2)
zlabel("")
gca().rotation_angles = [58 75];
xgrid

See also

• gammaln — Le logarithme de la fonction gamma.
• dlgamma — dérivée de la fonction gammaln ou fonction psi.
• cdfgam — fonction de répartition de la distribution gamma
• factorial — factorial function : product of the n first positive integers

History