- Scilab Help
- Control Systems - CACSD
- Linear System Representation
- abcd
- arma
- arma2p
- arma2ss
- armac
- bloc2ss
- cont_frm
- des2ss
- des2tf
- frep2tf
- lsslist
- markp2ss
- pfss
- pol2des
- sm2des
- sm2ss
- ss2des
- ss2ss
- ss2tf
- ss2zp
- ssprint
- ssrand
- sysconv
- sysdiag
- syslin
- syssize
- systmat
- tf2des
- tf2ss
- tf2zp
- trfmod
- zp2ss
- zp2tf
- zpk
- zpk2ss
- zpk2tf
Please note that the recommended version of Scilab is 2026.0.1. This page might be outdated.
See the recommended documentation of this function
ss2ss
state-space to state-space conversion, feedback, injection
Syntax
[Sl1, right, left] = ss2ss(Sl, T) [Sl1, right, left] = ss2ss(Sl, T, F) [Sl1, right, left] = ss2ss(Sl, T, F, G) [Sl1, right, left] = ss2ss(Sl, T, F, G, flag)
Arguments
- Sl
linear system (
syslinlist) in state-space form- T
square (non-singular) matrix
- Sl1, right, left
linear systems (syslin lists) in state-space form
- F
real matrix (state feedback gain)
- G
real matrix (output injection gain)
Description
Returns the linear system Sl1=[A1,B1,C1,D1] where
A1=inv(T)*A*T, B1=inv(T)*B, C1=C*T, D1=D.
Optional parameters F and G
are state feedback and output injection respectively.
For example, Sl1=ss2ss(Sl,T,F) returns
Sl1 with:
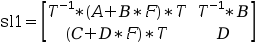
and right is a non singular linear system such
that Sl1=Sl*right.
Sl1*inv(right) is a factorization of
Sl.
Sl1=ss2ss(Sl,T,0*F,G) returns
Sl1 with:
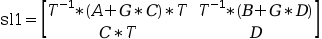
and left is a non singular linear system such
that Sl1=left*Sl (right=Id if
F=0).
When both F and G are given,
Sl1=left*Sl*right.
When
flagis used andflag=1an output injection as follows is used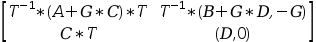
and then a feedback is performed,
Fmust be of size(m+p,n)
rightandlefthave the following property:When
flagis used andflag=2a feedback (Fmust be of size(m,n)) is performed and then the above output injection is applied.rightandlefthave the following property:
Examples
Sl=ssrand(2,2,5); trzeros(Sl) // zeros are invariant: Sl1=ss2ss(Sl,rand(5,5),rand(2,5),rand(5,2)); trzeros(Sl1), trzeros(rand(2,2)*Sl1*rand(2,2)) // output injection [ A + GC, (B+GD,-G)] // [ C , (D , 0)] p=1,m=2,n=2; sys=ssrand(p,m,n); // feedback (m,n) first and then output injection. F1=rand(m,n); G=rand(n,p); [sys1,right,left]=ss2ss(sys,rand(n,n),F1,G,2); // Sl1 equiv left*blockdiag(sys*right,eye(p,p))) res=clean(ss2tf(sys1) - ss2tf(left*blockdiag(sys*right,eye(p,p)))) // output injection then feedback (m+p,n) F2=rand(p,n); F=[F1;F2]; [sys2,right,left]=ss2ss(sys,rand(n,n),F,G,1); // Sl1 equiv left*blockdiag(sys,eye(p,p))*right res=clean(ss2tf(sys2)-ss2tf(left*blockdiag(sys,eye(p,p))*right)) // when F2= 0; sys1 and sys2 are the same F2=0*rand(p,n);F=[F1;F2]; [sys2,right,left]=ss2ss(sys,rand(n,n),F,G,1); res=clean(ss2tf(sys2)-ss2tf(sys1))
| Report an issue | ||
| << ss2des | Linear System Representation | ss2tf >> |