Please note that the recommended version of Scilab is 2026.0.1. This page might be outdated.
See the recommended documentation of this function
surf
Esboço de superfície 3d
Seqüência de Chamamento
surf() // sample surf(Z) surf(X, Y, Z) surf(X, Y, fun) surf(X, Y, list(fun, params)) surf(.., colors) surf(.., <GlobalProperty>) surf(.., colors, <GlobalProperty>) surf(axes_handle,...)
Parâmetros
- X,Y
two vectors of real numbers, of lengths
nxandny; or two real matrices of sizesnyxnx: They define the data grid (horizontal coordinates of the grid nodes). All grid cells are quadrangular but not necessarily rectangular.By default,
X = 1:size(Z,2)andY = 1:size(Z,1)are used.- Z
uma matriz real definindo as alturas da superfície. Não pode ser omitida. O dado Z é uma matriz
nyxnx.- fun
handle of a function, as in
surf(x,y, myFun)where the expected syntax ofmyFunisZ=myFun(X,Y).If the 2D function
funto plot needs some parameters as input arguments, the function and its parameters can be specified through a list, as insurf(x,y, list(delip, -0.4))orsurf(x,y, list(myfun, a,b))withZ = myFun(X,Y, a,b)If
Xor/andYare grid-generating vectors whilefun(…)expects only input matrices,surf(…)automatically generates matrices fromXor/andYand properly callsfun(…).- colors
um matriz de reais opcional definindo valores de cores para cada ponto
(X(j),Y(i))do grid (ver descrição abaixo).- <GlobalProperty>
esta propriedade rerpresenta uma seqüência de pares de sentenças
{PropertyName,PropertyValue}que definem propriedades globais de objetos aplicadas a todas as curvas criadas neste esboço. Para uma completa visualização das propriedades disponíveis veja GlobalProperty.- <axes_handle>
este argumento opcional força os eixos a aparecerem dentro dos eixos selecionados dados por
axes_handleao invés dos eixos correntes (ver gca).
Descrição
surf desenha uma superfície parametrizada
colorida utilizando um grid retangular definido pelas coordenadas
X e Y
surf foi criada para lidar melhor
com a sintaxe do Matlab. Para melhorar a compatibilidade gráfica, usuários
do Matlab devem utilizar surf (ao invés de plot3d).
Especificação de entrada de dados:
Neste parágrafo, e para sermos mais claros, não mencionaremos os
argumentos opcionais de GlobalProperty ojá que eles não
interferem na entrada de dados (exceto pelas propriedades
"Xdata", "Ydata" e
"Zdata", ver GlobalProperty). É assumido que todos
estes argumentos opcionais podem estar presentes também.
X or Y can be :
a) um vetor: se
Xfor um vetor, length(X)=nx. Respectivamente, seYfor um vetor, length(Y)=ny.b) uma matriz: neste caso, size(
X) (ou size(Y)) deve ser igual a size(Z).
Especificação de entrada de cores:
Como citado acima, a superfície é criada sobre um gride retangular
de apoio. Consideremos duas variáveis independentes i e
j tais que:
a) 1 <= i <= ny and 1 <= j <= nx
b) i-1,j-1 ---- i-1,j ---- i-1,j+1 ---… |
| | | | i direction
i,j-1 ----- i,j ----- i,j+1 ---… |
| | | |
: : :
............> j direction
Este grid retangular imaginário é utilizado para se contruir o
suporte da superfície real sobre o plano XY . De fato,
os dados X,Y e Z
possuem o mesmo tamanho (mesmo se X ou
Y for um vetor, ver abaixo) e podem ser considerados
como três funções x(i,j), y(i,j) e
z(i,j) especificando a superficie desejada. Se
X ou Y forem vetores, eles são
internamente tratados para produzir boas matrizes de dimensões
correspondentes às dimensões da matriz Z (e o grid é
forçosamente uma região retangular).
Considerando as três funções x(i,j),
y(i,j) e z(i,j), a porção da
superfície definida entre dois i e j
consecutivos é chamada remendo.
Por padrão, quando nenhuma matriz de cores é adicionada a uma
chamada a surf, o parâmetro de cor é ligado o dado Z .
Quando uma matriz de cores colors é dada, pode ser
aplicada aos remendos de duas formas diferentes: nos vértices, ou no
centro de cada remendo.
É por isto que, se Z é uma matriz
[nyxnx] , a dimensão da matriz
colors C pode ser
[nyxnx] (uma cor definida por vértice)
ou [ny-1xnx-1] (uma cor definida por
remendo).
A representação de cores também varia quando se especifica algumas GlobalProperties (propriedades globais):
A propriedade FaceColor ajusta o padrão de
gradação: pode ser 'interp' ou
'flat' (modo padrão). Quando
'interp' é selecionado, é realizado uma interpolação
bilinear de cores no remendo. Se size(C) é igual a
size(Z)-1 (i.e. for fornecida apenas uma cor ao
remendo) então a cor dos vértices definindo o remendo é ajustada para a
dada cor do remendo.
Quando 'flat' (modo padrão) é habilitado, é
utilizada uma representação de cores de facetadas (uma cor por remendo).
Se size(C) é igual a size(Z) (i.e.
foi fornecida apenas uma cor por os vértices), as últimas linha e coluna
de C são ignoradas.
Os argumentos GlobalProperty devem ser usados
para customizar a superfície. Aqui está uma breve descrição de como
funcionam:
- GlobalProperty
esta opção pode ser utilizada para especificar como todas as superfícies serão desenhadas. Deve sempre ser um par de sentenças constituidos de um string definindo
PropertyName, (nome da propriedade) e seu valor associadoPropertyValue(que pode ser um inteiro ou outra coisa... dependendo do tipo dePropertyName). Note que você pode ajustar múltiplas propriedades : a cor da face e da borda, dados de cores, mapeamento de dados de cores, cor do marcador (plano de fundo e primeiro plano), visibilidade, recorte, espessura das bordas da superfície... (ver GlobalProperty )Note que todas essas propriedades podem ser (re-)ajustadas através das propriedades da entidade superfície (ver surface_properties).
 | Por padrão, esboços sucessivos de superfície são superpostos. Para
limpar o esboço anteirior, use clf(). Para habilitar o
modo auto_clear (limpeza automática) como modo padrão,
edite seus eixos padrões fazendo: gda().auto_clear = 'on'
Entre com o comando surf() para visualizar uma demonstração. |
Exemplos
With a function:
function z=mySurf(x, y, a, b) if ~isdef("a","l"), a = 1, end if ~isdef("b","l"), b = 1, end z = a*x.*sin(y) + b*y.*cos(x); endfunction clf subplot(121), surf(-5:0.2:5, -3:0.2:3, mySurf) // without parameters subplot(122), surf(-5:0.2:5, -3:0.2:3, list(mySurf, 2,-1)) // with parameters gcf().color_map = jetcolormap(100); set(gcf(), "axes_size", [800 350], "rotation_style","multiple"); gca().rotation_angles = [40 -60];
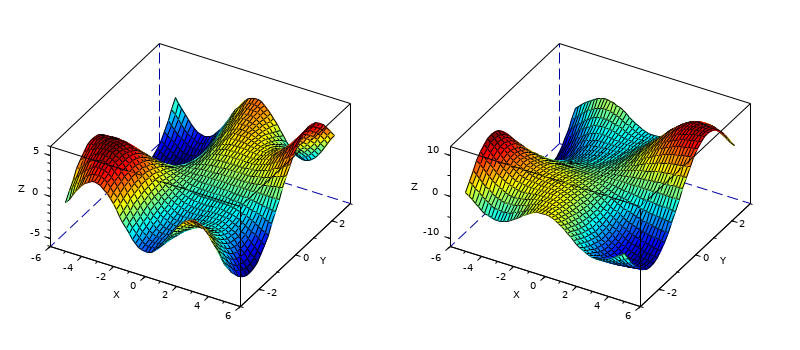
surf(Z):
// inicialização de Z Z =[0.0001 0.0013 0.0053 -0.0299 -0.1809 -0.2465 -0.1100 -0.0168 -0.0008 -0.0000 0.0005 0.0089 0.0259 -0.3673 -1.8670 -2.4736 -1.0866 -0.1602 -0.0067 0.0000 0.0004 0.0214 0.1739 -0.3147 -4.0919 -6.4101 -2.7589 -0.2779 0.0131 0.0020 -0.0088 -0.0871 0.0364 1.8559 1.4995 -2.2171 -0.2729 0.8368 0.2016 0.0130 -0.0308 -0.4313 -1.7334 -0.1148 3.0731 0.4444 2.6145 2.4410 0.4877 0.0301 -0.0336 -0.4990 -2.3552 -2.1722 0.8856 -0.0531 2.6416 2.4064 0.4771 0.0294 -0.0137 -0.1967 -0.8083 0.2289 3.3983 3.1955 2.4338 1.2129 0.2108 0.0125 -0.0014 -0.0017 0.3189 2.7414 7.1622 7.1361 3.1242 0.6633 0.0674 0.0030]; clf // superfície simples subplot(121) surf(Z); // note que X e Y são determinados pelas dimensões de Z // a mesma superfície com faces vermelhas e bordas azuis subplot(122) surf(Z,'facecol','red','edgecol','blu'); gcf().axes_size = [850 400];
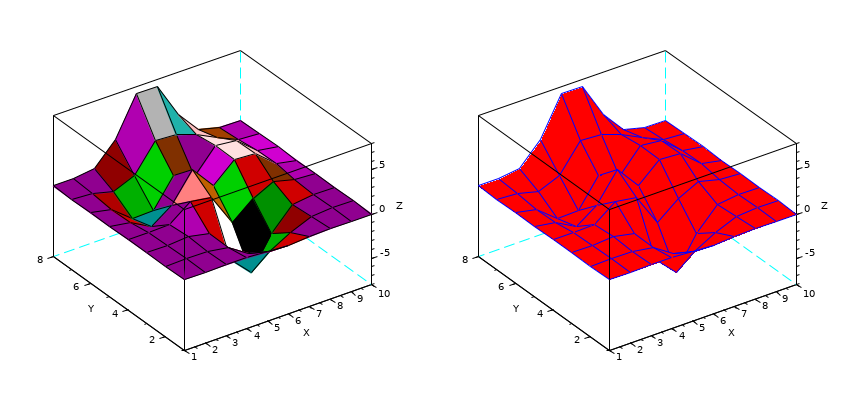
surf(X, Y, Z):
// inicialização de X e Y // NB: aqui, X tem as mesmas linhas e Y tem as mesmas colunas X=[-3.0000 -2.3333 -1.6667 -1.0000 -0.3333 0.3333 1.0000 1.6667 2.3333 3.0000 -3.0000 -2.3333 -1.6667 -1.0000 -0.3333 0.3333 1.0000 1.6667 2.3333 3.0000 -3.0000 -2.3333 -1.6667 -1.0000 -0.3333 0.3333 1.0000 1.6667 2.3333 3.0000 -3.0000 -2.3333 -1.6667 -1.0000 -0.3333 0.3333 1.0000 1.6667 2.3333 3.0000 -3.0000 -2.3333 -1.6667 -1.0000 -0.3333 0.3333 1.0000 1.6667 2.3333 3.0000 -3.0000 -2.3333 -1.6667 -1.0000 -0.3333 0.3333 1.0000 1.6667 2.3333 3.0000 -3.0000 -2.3333 -1.6667 -1.0000 -0.3333 0.3333 1.0000 1.6667 2.3333 3.0000 -3.0000 -2.3333 -1.6667 -1.0000 -0.3333 0.3333 1.0000 1.6667 2.3333 3.0000 -3.0000 -2.3333 -1.6667 -1.0000 -0.3333 0.3333 1.0000 1.6667 2.3333 3.0000 -3.0000 -2.3333 -1.6667 -1.0000 -0.3333 0.3333 1.0000 1.6667 2.3333 3.0000]; Y=[-3.0000 -3.0000 -3.0000 -3.0000 -3.0000 -3.0000 -3.0000 -3.0000 -3.0000 -3.0000 -2.3333 -2.3333 -2.3333 -2.3333 -2.3333 -2.3333 -2.3333 -2.3333 -2.3333 -2.3333 -1.6667 -1.6667 -1.6667 -1.6667 -1.6667 -1.6667 -1.6667 -1.6667 -1.6667 -1.6667 -1.0000 -1.0000 -1.0000 -1.0000 -1.0000 -1.0000 -1.0000 -1.0000 -1.0000 -1.0000 -0.3333 -0.3333 -0.3333 -0.3333 -0.3333 -0.3333 -0.3333 -0.3333 -0.3333 -0.3333 0.3333 0.3333 0.3333 0.3333 0.3333 0.3333 0.3333 0.3333 0.3333 0.3333 1.0000 1.0000 1.0000 1.0000 1.0000 1.0000 1.0000 1.0000 1.0000 1.0000 1.6667 1.6667 1.6667 1.6667 1.6667 1.6667 1.6667 1.6667 1.6667 1.6667 2.3333 2.3333 2.3333 2.3333 2.3333 2.3333 2.3333 2.3333 2.3333 2.3333 3.0000 3.0000 3.0000 3.0000 3.0000 3.0000 3.0000 3.0000 3.0000 3.0000]; Z= [0.0001 0.0013 0.0053 -0.0299 -0.1809 -0.2465 -0.1100 -0.0168 -0.0008 -0.0000 0.0005 0.0089 0.0259 -0.3673 -1.8670 -2.4736 -1.0866 -0.1602 -0.0067 0.0000 0.0004 0.0214 0.1739 -0.3147 -4.0919 -6.4101 -2.7589 -0.2779 0.0131 0.0020 -0.0088 -0.0871 0.0364 1.8559 1.4995 -2.2171 -0.2729 0.8368 0.2016 0.0130 -0.0308 -0.4313 -1.7334 -0.1148 3.0731 0.4444 2.6145 2.4410 0.4877 0.0301 -0.0336 -0.4990 -2.3552 -2.1722 0.8856 -0.0531 2.6416 2.4064 0.4771 0.0294 -0.0137 -0.1967 -0.8083 0.2289 3.3983 3.1955 2.4338 1.2129 0.2108 0.0125 -0.0014 -0.0017 0.3189 2.7414 7.1622 7.1361 3.1242 0.6633 0.0674 0.0030 0.0002 0.0104 0.1733 1.0852 2.6741 2.6725 1.1119 0.1973 0.0152 0.0005 0.0000 0.0012 0.0183 0.1099 0.2684 0.2683 0.1107 0.0190 0.0014 0.0000]; scf(3) surf(X,Y,Z)
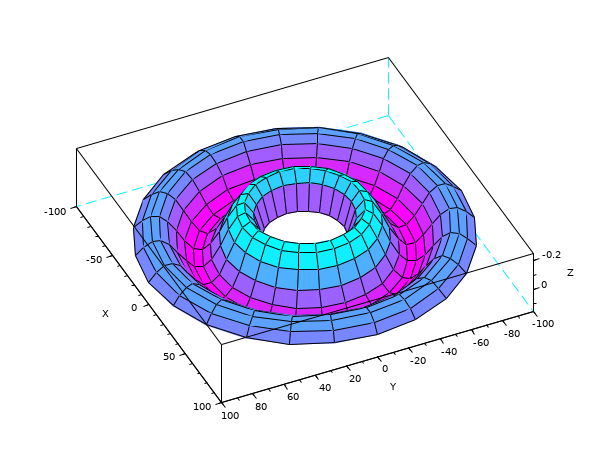
surf(X,Y,Z) on a cylindrical grid.. Facets are still quadrangular:
theta = 0:15:360; r = 25:5:100; [R,T] = ndgrid(r,theta); X = R.*cosd(T); Y = R.* sind(T); Z = sinc(R/8); clf surf(X, Y, Z) gcf().color_map = coolcolormap(50); gca().rotation_angles=[195 -155];
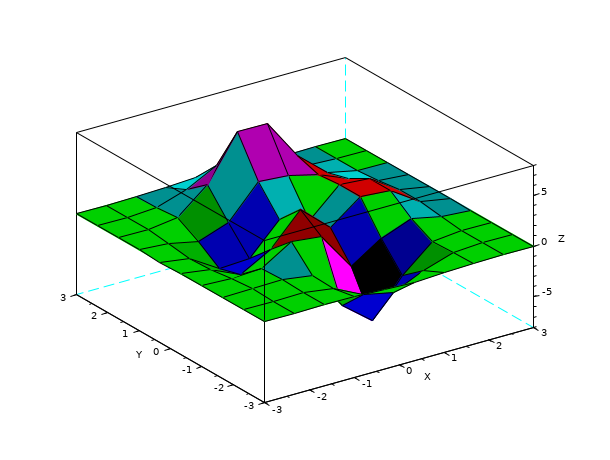
// exemplo 3 // X e Y são vetores => mesmo comportamento que a amostra 1 // com vetores, o grid é inevitavelmente retangular scf(5)// nova figura de número 5 X = [-3.0000 -2.3333 -1.6667 -1.0000 -0.3333 0.3333 1.0000 1.6667 2.3333 3.0000]; Y = X; surf(X,Y,Z) //exemplos com LineSpec e GlobalProperty: xdel(winsid()) // destruindo todas as figuras existentes surf(Z,Z+5) // array de cores especificado e=gce(); e.cdata_mapping='direct' // o padrão é 'scaled' relativo ao mapa de cores colormap e.color_flag=3; // modo de gradação interpolada. O padrão é 4 (modo 'flat') para surf scf(2) surf(X,Y,Z,'colorda',ones(10,10),'edgeco','cya','marker','penta','markersiz',20,'markeredg','yel','ydata',56:65) scf(3) surf(Z,'cdatamapping','direct') scf(4) surf(Z,'facecol','interp') // interpolated shading mode (color_flag == 3) scf(10) axfig10=gca(); scf(11); surf(axfig10,Z,'ydat',[100:109],'marker','d','markerfac','green','markeredg','yel') // draw onto the axe of figure 10
Ver Também
- plot2d — 2D plot
- clf — Clears and resets a figure or a frame uicontrol
- xdel — deleta uma janela de gráficos
- delete — Deleta uma entidade gráfica e seus galhos
- LineSpec — Customização rápida de linhas que aparecem em um esboço
- GlobalProperty — Customização de aparência dos objetos (curvas, superfícies...) num comando plot ou surf.
Histórico
| Version | Description |
| 6.0.2 | The "Foreground", "markForeground", and "markBackground" global properties colors can now be specified as named colors chosen in the full predefined colors list, or by their "#RRGGBB" hexadecimal codes, or by their colormap indices. surf(X,Y,fun..) and surf(X,Y,list(fun, params)) syntaxes added. |
| Report an issue | ||
| << secto3d | 3d_plot | surface properties >> |