Please note that the recommended version of Scilab is 2026.0.1. This page might be outdated.
See the recommended documentation of this function
bsplin3val
3次元スプラインの任意微分評価関数
呼び出し手順
[dfp]=bsplin3val(xp,yp,zp,tl,der)
引数
- xp, yp, zp
同じ大きさの実数ベクトルまたは行列
- tl
"splin3d"型のtlistで, 3次元テンソルスプライン(以下では
sと 呼びます)を定義します.- der
3つ要素
[ox,oy,oz]のベクトルで, 計算するsの微分を定義します.- dfp
xp,ypおよびzpと同じ大きさのベクトルまたは行列で, これらの点におけるsの要素毎に特定の微分の評価値.
説明
関数interp3dは
スプラインsとその1階の微分のみを計算しますが,
bsplin3valはs
の任意の微分値を計算することができます.
計算する微分値は引数der=[ox,oy,oz]で
指定されます :
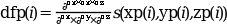
この場合,der=[0 0 0] は
s, der=[1 0 0]は
ds/dx, der=[0 1 0] は
ds/dy, der=[1 1 0]は
d2s/dxdy, など...に対応します
座標がグリッドの外部の点 (xp(i),yp(i),zp(i))の場合,関数は0を返します.
例
deff("v=f(x,y,z)","v=cos(x).*sin(y).*cos(z)"); deff("v=fx(x,y,z)","v=-sin(x).*sin(y).*cos(z)"); deff("v=fxy(x,y,z)","v=-sin(x).*cos(y).*cos(z)"); deff("v=fxyz(x,y,z)","v=sin(x).*cos(y).*sin(z)"); deff("v=fxxyz(x,y,z)","v=cos(x).*cos(y).*sin(z)"); n = 20; // n x n x n 補間点 x = linspace(0,2*%pi,n); y=x; z=x; // 補間グリッド [X,Y,Z] = ndgrid(x,y,z); V = f(X,Y,Z); tl = splin3d(x,y,z,V,[5 5 5]); // ある点で f および微係数を計算し, // スプライン補間値と比較 xp = grand(1,1,"unf",0,2*%pi); yp = grand(1,1,"unf",0,2*%pi); zp = grand(1,1,"unf",0,2*%pi); f_e = f(xp,yp,zp) f_i = bsplin3val(xp,yp,zp,tl,[0 0 0]) fx_e = fx(xp,yp,zp) fx_i = bsplin3val(xp,yp,zp,tl,[1 0 0]) fxy_e = fxy(xp,yp,zp) fxy_i = bsplin3val(xp,yp,zp,tl,[1 1 0]) fxyz_e = fxyz(xp,yp,zp) fxyz_i = bsplin3val(xp,yp,zp,tl,[1 1 1]) fxxyz_e = fxxyz(xp,yp,zp) fxxyz_i = bsplin3val(xp,yp,zp,tl,[2 1 1])
履歴
| Version | Description |
| 5.4.0 | 以前は,入力引数の虚部は暗黙的に無視されていました. |
| Report an issue | ||
| << Interpolation | Interpolation | cshep2d >> |