引数

x

実数または複素数のベクトル.

alpha

r実数ベクトル

ice

整数フラグ, デフォルト値: 0

K

整数, 指定可能な値は 1 または 2, ハンケル関数の型.

説明

• besseli(alpha,x) は, 実数の次数alpha および引数 xに関する 第1種修正ベッセル関数(I_α)を計算します, besseli(alpha,x,1) は besseli(alpha,x).*exp(-abs(real(x)))を計算します.

• besselj(alpha,x) は第1種のベッセル関数(J_α)を 実数の次数alpha および引数 xに関して 計算します. besselj(alpha,x,1) は besselj(alpha,x).*exp(-abs(imag(x)))を計算します.

• besselk(alpha,x) は第2種修正ベッセル関数 (K_α)を 実数の次数alpha および引数 xに関して 計算します. besselk(alpha,x,1) は besselk(alpha,x).*exp(x)を計算します.

• bessely(alpha,x)は第2種のベッセル関数(Y_α)を 実数の次数alpha および引数 xに関して 計算します. bessely(alpha,x,1) は bessely(alpha,x).*exp(-abs(imag(x)))を計算します.

• besselh(alpha [,K] ,x) は第3種のベッセル関数 (Kに依存してハンケル関数 H1 または H2)を 実数の次数alpha および引数 xに関して 計算します.Kが省略された場合, 1に等しいと仮定されます. besselh(alpha,1,x,1)は besselh(alpha,1,x).*exp(-%i*x)を計算し, besselh(alpha,2,x,1) は besselh(alpha,2,x).*exp(%i*x)を計算します.

注意

alphaおよび xが同じ大きさの 配列の場合,結果yも同じ大きさとなります. 入力のどちらかがスカラーの場合, もう片方の大きさにまで拡張されます. 片方の入力が行ベクトルでもう片方が列ベクトルの場合, 結果yは関数値の二次元テーブルとなります.

Y_α および J_α ベッセル関数はベッセルの微分方程式の 2つの独立解です:

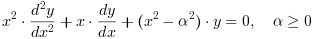
修正ベッセル関数K_α および I_αは 修正ベッセル微分方程式の2つの独立解です:

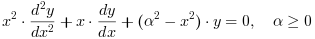
H_α¹ および H_α²は第1種および第2種のハンケル関数 で,第1種および第2種のベッセル関数の線形結合です:

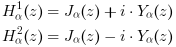
例

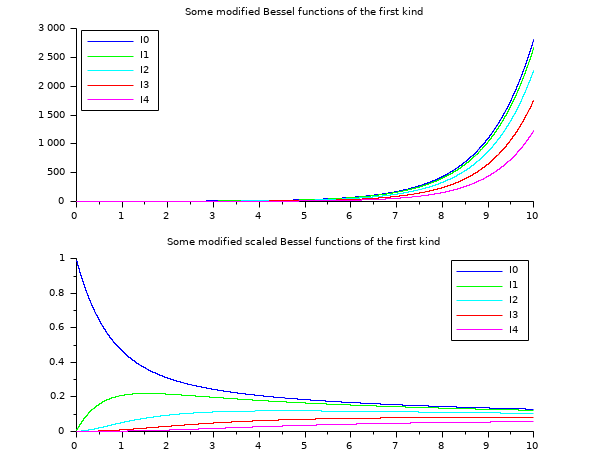
//  besselI 関数
// ==================
   x = linspace(0.01,10,5000)';
   clf()
   subplot(2,1,1)
   plot2d(x,besseli(0:4,x), style=2:6)
   legend('I'+string(0:4),2);
   xtitle("Some modified Bessel functions of the first kind")
   subplot(2,1,2)
   plot2d(x,besseli(0:4,x,1), style=2:6)
   legend('I'+string(0:4),1);
   xtitle("Some modified scaled Bessel functions of the first kind")

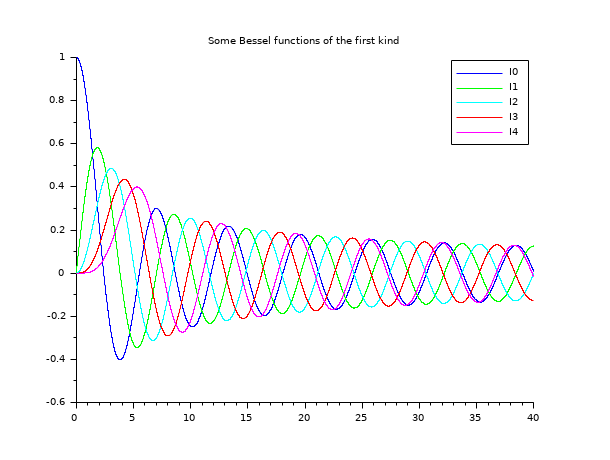
// besselJ 関数
// =================
   x = linspace(0,40,5000)';
   clf()
   plot2d(x,besselj(0:4,x), style=2:6, leg="J0@J1@J2@J3@J4")
   legend('I'+string(0:4),1);
   xtitle("Some Bessel functions of the first kind")

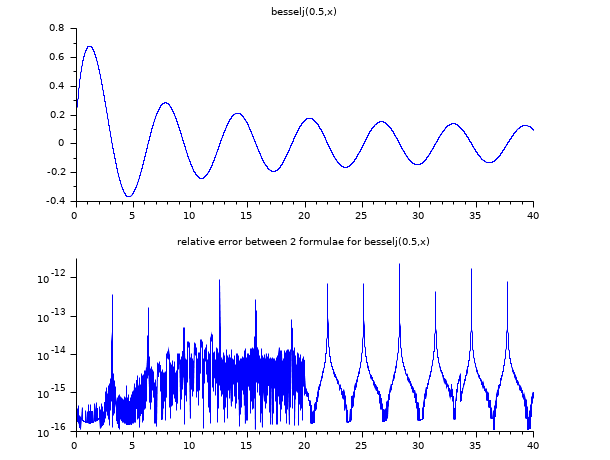
// J_(1/2)(x) = sqrt(2/(x pi)) sin(x)　の関係を用いて
//  besselj(0.5,x) のアルゴリズムをより直接的な式と比較します
   x = linspace(0.1,40,5000)';
   y1 = besselj(0.5, x);
   y2 = sqrt(2 ./(%pi*x)).*sin(x);
   er = abs((y1-y2)./y2);
   ind = find(er > 0 & y2 ~= 0);
   clf()
   subplot(2,1,1)
   plot2d(x,y1,style=2)
   xtitle("besselj(0.5,x)")
   subplot(2,1,2)
   plot2d(x(ind), er(ind), style=2, logflag="nl")
   xtitle("relative error between 2 formulae for besselj(0.5,x)")

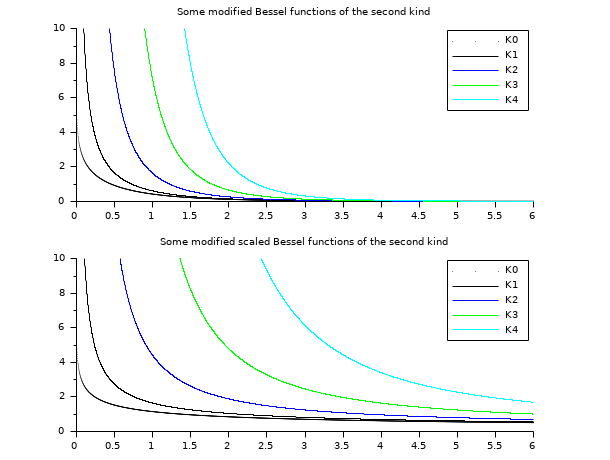
// besselK 関数
// =================
   x = linspace(0.01,10,5000)';
   clf()
   subplot(2,1,1)
   plot2d(x,besselk(0:4,x), style=0:4, rect=[0,0,6,10])
   legend('K'+string(0:4),1);
   xtitle("Some modified Bessel functions of the second kind")
   subplot(2,1,2)
   plot2d(x,besselk(0:4,x,1), style=0:4, rect=[0,0,6,10])
   legend('K'+string(0:4),1);
   xtitle("Some modified scaled Bessel functions of the second kind")

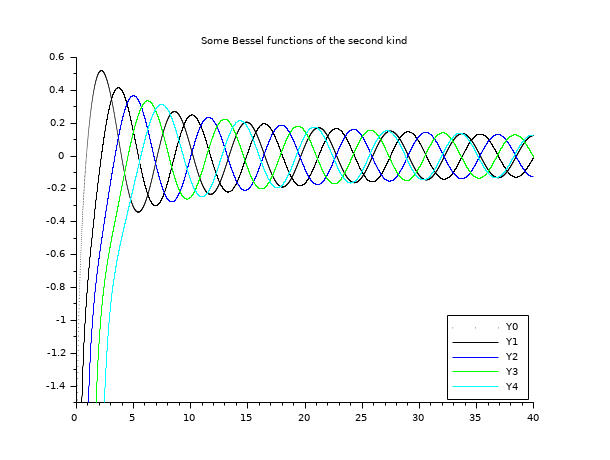
// besselY 関数
// =================
   x = linspace(0.1,40,5000)'; // Y ベッセル関数は x -> 0+ については制限されません
   clf()
   plot2d(x,bessely(0:4,x), style=0:4, rect=[0,-1.5,40,0.6])
   legend('Y'+string(0:4),4);
   xtitle("Some Bessel functions of the second kind")

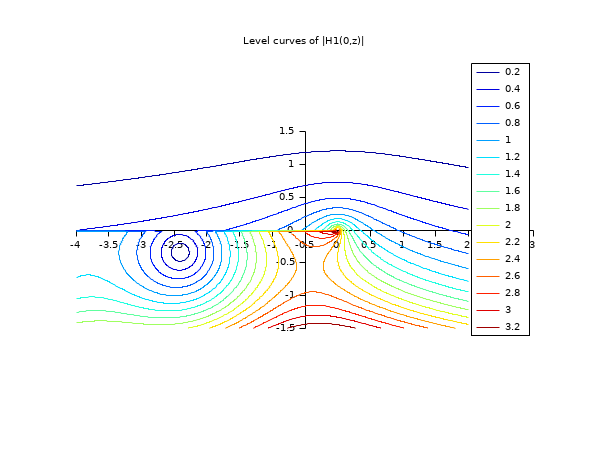
// besselH 関数
// =================
   x=-4:0.025:2; y=-1.5:0.025:1.5;
   [X,Y] = ndgrid(x,y);
   H = besselh(0,1,X+%i*Y);
   clf();f=gcf();
   xset("fpf"," ")
   f.color_map=jetcolormap(16);
   contour2d(x,y,abs(H),0.2:0.2:3.2,strf="034",rect=[-4,-1.5,3,1.5])
   legends(string(0.2:0.2:3.2),1:16,"ur")
   xtitle("Level curves of |H1(0,z)|")

使用される関数

ソースコードは SCI/modules/special_functions/src/fortran/slatec および SCI/modules/special_functions/src/fortran にあります

Slatec : dbesi.f, zbesi.f, dbesj.f, zbesj.f, dbesk.f, zbesk.f, dbesy.f, zbesy.f, zbesh.f

拡張定義領域(Serge Steer INRIA)のドライバ (Serge Steer INRIA): dbesig.f, zbesig.f, dbesjg.f, zbesjg.f, dbeskg.f, zbeskg.f, dbesyg.f, zbesyg.f, zbeshg.f