CVode

CVode (abréviation de "C-language Variable-coefficients ODE solver") est un solveur numérique fournissant une méthode efficace et stable pour résoudre des Problèmes à Valeur Initiale d'Equations Différentielles Ordinarires (EDOs). Il utilise BDF ou Adams comme méthode d'intégration, et des itérations fonctionnelles ou de Newton.

Description

Appelé par xcos, CVode (abréviation de "C-language Variable-coefficients ODE solver") est un solveur numérique fournissant une méthode efficace et stable pour résoudre des Problèmes à Valeur Initiale de la forme :

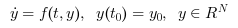
$\begin{eqnarray} \dot{y} = f(t,y), \hspace{3 mm} y(t_0) = y_0, \hspace{3 mm} y \in R^N \end{eqnarray}$

Partant de y₀ , CVode approxime y_n+1 grâce à la formule :

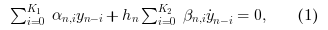
$\begin{eqnarray} \sum_{i=0}^{K_1} \alpha_{n,i} y_{n-i} + h_n\sum_{i=0}^{K_2} \beta_{n,i} \dot{y}_{n-i} = 0,\hspace{10 mm} (1) \end{eqnarray}$

avec y_n l'approximation de y(t_n) , et h_n = t_n - t_n-1 la taille du pas de temps.

Ces méthodes implicites sont caractérisées par leur ordre q, qui indique le nombre de points intermédiaires requis pour le calcul de y_n+1 .

C'est ici qu'intervient la différence entre BDF et Adams ("Backward Differentiation Formula" et "Adams-Moulton formula"):

Si le problème est raide, il est préférable d'utiliser BDF :

q, l'ordre de la méthode, est initialisé entre 1 et 5 (automatique),
K1 = q et K2 = 0.

Dans le cas non-raide, on préferera Adams :

q est initialisé entre 1 et 12 (automatique),
K1 = 1 et K2 = q.

Les coefficients sont fixes, déterminés uniformément par le type de méthode, son ordre, les pas de temps et la normalisation α_{n, 0} = -1 .

Quelque soit le choix et à chaque pas, injecter cette intégration dans (1) donne le système non-linéaire:

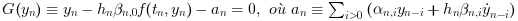
$G(y_n)\equiv y_n-h_n\beta_{n,0}f(t_n,y_n)-a_n=0, \hspace{2 mm} où \hspace{2 mm} a_n\equiv \sum_{i>0} (\alpha_{n,i} y_{n-i} + h_n\beta_{n,i}\dot{y}_{n-i})$

Ce système peut être résolu par des itérations fonctionnelles ou de Newton, décrites ci-après.

Dans les deux cas suivants, le y_n(0) initial "prédit" est calculé explicitement grâce aux valeurs passées, en ajoutant des dérivées.

Fonctionnelles : cette méthode n'implique que des évaluations de f, elle calcule y_n(0) simplement en itérant la formule :
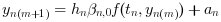
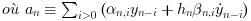
$y_{n(m+1)} = h_n β_{n,0} f(t_n,y_{n(m)}) + a_n$ $où \hspace{2 mm} a_n\equiv \sum_{i>0} (\alpha_{n,i} y_{n-i} + h_n\beta_{n,i}\dot{y}_{n-i})$

Newton : ici, nous utilisons un solveur direct dense sur le système linéaire :
$M[y_{n(m+1)}-y_{n(m)}]=-G(y_{n(m)}), \hspace{4 mm} M \approx I-\gamma J, \hspace{2 mm} J=\frac{\partial f}{\partial y}, \hspace{2 mm} et \hspace{2 mm} \gamma = h_n\beta_{n,0}$

Dans les deux cas, CVode se sert des valeurs passées pour contrôler l'erreur locale y_n(m) - y_n(0) et recalcule h_n si l'erreur n'est pas satisfaisante.

Les choix recommandés sont BDF / Newton pour les problèmes raides et Adams / Functional pour les non-raides.

Le solveur est appelé entre les activations, parce-qu'une activation est susceptible de modifier le système.

Suivant la criticalité de l'événement (son effet sur le problème continu), soit le solveur poursuit avec temps initial et final différents comme si rien ne s'était passé, soit, si le système a été modifié, il faut "réinitialiser à froid" le solveur et le relancer.

En moyenne, CVode accepte des tolérances jusqu'à 10^-16. Au-delà, il retourne l'erreur Trop de précision demandée.

Exemples

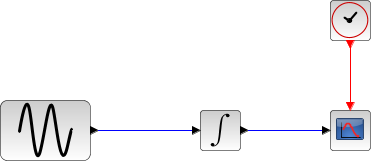
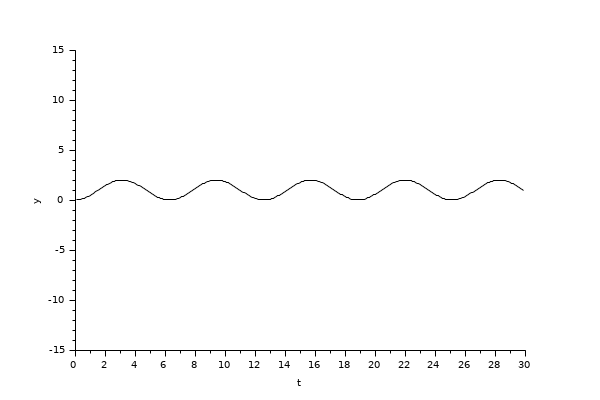
Le bloc intégrale retourne son état continu, on peut l'évaluer avec BDF / Newton en lançant l'exemple :

// Import du diagramme et réglage du temps final
loadScicos();
loadXcosLibs();
importXcosDiagram("SCI/modules/xcos/examples/solvers/ODE_Example.zcos");
scs_m.props.tf = 5000;

// Sélection de BDF / Newton
scs_m.props.tol(6) = 1;

// Lancement du chrono, de la simulation et affichage du temps
tic();
try xcos_simulate(scs_m, 4); catch disp(lasterror()); end
t = toc();
disp("Temps pour BDF / Newton :", t);

La console Scilab affiche :

Temps pour BDF / Newton:
 13.438

Maintenant, dans le script suivant, on compare la différence de temps entre les méthodes en lançant l'exemple avec les quatre solveurs tour à tour : Ouveture du script

Résultats :

Temps pour BDF / Newton :
 18.894

Temps pour BDF / Functional :
 18.382

Temps pour Adams / Newton :
 10.368

Temps pour Adams / Functional :
 9.815

Les résultats montrent que pour un problème continu non-raide simple, Adams / Functional est le plus rapide.

Voir Aussi

Bibliographie

Documentation Sundials

Report an issue
<< LSodar	Solveurs	Runge-Kutta 4(5) >>

Copyright (c) 2022-2024 (Dassault Systèmes)
Copyright (c) 2017-2022 (ESI Group)
Copyright (c) 2011-2017 (Scilab Enterprises)
Copyright (c) 1989-2012 (INRIA)
Copyright (c) 1989-2007 (ENPC)
with contributors

Last updated:
Tue Feb 25 08:50:44 CET 2020