Please note that the recommended version of Scilab is 2026.0.1. This page might be outdated.
See the recommended documentation of this function
LSodar
LSodar (abréviation de "Livermore Solver for Ordinary Differential equations, with Automatic method switching for stiff and nonstiff problems, and with Root-finding") est un solveur numérique fournissant une méthode efficace et stable pour résoudre des Problèmes à Valeur Initiale d'Equations Différentielles Ordinaires (EDOs).
Description
Appelé par xcos, LSodar (abréviation de "Livermore Solver for Ordinary Differential equations, with Automatic method switching for stiff and nonstiff problems, and with Root-finding") est un solveur numérique fournissant une méthode efficace et stable pour résoudre des Problèmes à Valeur Initiale d'Equations Différentielles Ordinaires (EDOs) de la forme :
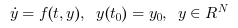
LSodar est similaire à CVode sur de nombreux points:
- Son pas de temps est variable,
- Il est capable d'utiliser les méthodes d'intégration BDF et Adams,
- BDF et Adams étant des méthodes implicites stables, LSodar convient aussi bien à des problèmes raides que non-raides,
- Ils recherchent tous deux des racines sur l'intervalle.
La principale différence est que LSodar est automatisé, et choisit lui-même entre BDF et Adams, en vérifiant la raideur du problème à chaque pas.
Si le pas est considéré raide, alors BDF (avec ordre max = 5) est utilisé et la méthode de Newton modifiée 'Chord' iteration est sélectionnée.
Sinon, le programme utilise l'intégration d'Adams (avec ordre max = 12) et des itérations fonctionnelles (Functional).
La détection de raideur est effectuée par tentatives de pas et comparaison avec chaque méthode.
D'abord, si nous sommes actuellement en mode Adams et l'ordre est supérieur à 5, alors on considère le problème comme non-raide et on poursuit avec Adams.
Les vingt premiers pas utilisent la méthode Adams / Functional. Ensuite, LSodar calcule le pas idéal avec chaque méthode. Si le gain est d'au moins ratio = 5, alors la méthode actuelle est changée (Adams / Functional pour BDF / Chord Newton ou vice-versa).
Après chaque changement, LSodar passe vingt étapes, puis recommence à calculer les pas à chaque étape.
Une telle stratégie implique évidemment un ajout de calculs si la raideur du système est connue, mais est très efficace sur des problèmes qui requièrent une précision différenciée. Par exemple, les problèmes sensibles aux discontinuités.
Concernant la précision, les deux méthodes d'intégration/itération étant proches de celles de CVode, les résultats sont très similaires.
Exemples
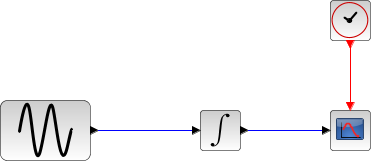
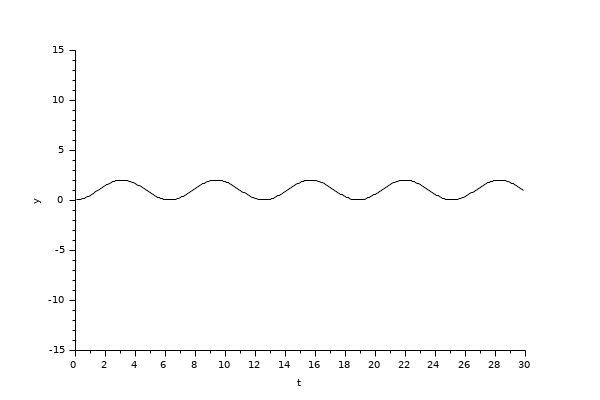
Le bloc intégrale retourne son état continu, on peut l'évaluer avec LSodar en lançant l'exemple :
// Import du diagramme et réglage du temps final loadScicos(); loadXcosLibs(); importXcosDiagram("SCI/modules/xcos/examples/solvers/ODE_Example.zcos"); scs_m.props.tf = 5000; // Sélection de LSodar scs_m.props.tol(6) = 0; // Lancement du chrono, de la simulation et affichage du temps tic(); try xcos_simulate(scs_m, 4); catch disp(lasterror()); end t = toc(); disp("Temps pour LSodar :",t);
La console Scilab affiche :
Temps pour LSodar:
9.546
Maintenant, dans le script suivant, on compare la différence de temps entre LSodar et CVode en lançant l'exemple avec les cinq solveurs tour à tour : Ouverture du script
Temps pour LSodar :
6.115
Temps pour BDF / Newton :
18.894
Temps pour BDF / Functional :
18.382
Temps pour Adams / Newton :
10.368
Temps pour Adams / Functional :
9.815
Ces résultats montrent que pour un problème non-raide, à même précision demandée, LSodar est significativement plus rapide. D'autres tests ont montré la proximité des résultats. En effet, on trouve que l'écart entre les solutions de LSodar et CVode est de l'ordre de la plus haute tolérance ( ylsodar - ycvode ≈ max(reltol, abstol) ).
Les solveurs d'EDO à pas variable ne sont pas appropriés pour des applications temps réel déterministes car le surplus de calcul au passage d'un pas de temps varie au cours de l'application.
Voir Aussi
- CVode — CVode (abréviation de "C-language Variable-coefficients ODE solver") est un solveur numérique fournissant une méthode efficace et stable pour résoudre des Problèmes à Valeur Initiale d'Equations Différentielles Ordinarires (EDOs). Il utilise BDF ou Adams comme méthode d'intégration, et des itérations fonctionnelles ou de Newton.
- IDA — "Implicit Differential Algebraic equations system solver" est un solveur numérique fournissant une méthode efficace et stable pour résoudre des Problèmes à Valeur Initiale d'Equations Différentielles Algebriques (EDAs).
- Runge-Kutta 4(5) — Runge-Kutta est un solveur numérique fournissant une méthode explicite efficace pour résoudre des Problèmes à Valeur Initiale d'Equations Différentielles Ordinarires (EDOs).
- Dormand-Prince 4(5) — Dormand-Prince est un solveur numérique fournissant une méthode explicite efficace pour résoudre des Problèmes à Valeur Initiale d'Equations Différentielles Ordinarires (EDOs).
- Runge-Kutta Implicite 4(5) — Solveur numérique fournissant une méthode implicite efficace et stable pour résoudre des Problèmes à Valeur Initiale d'Equations Différentielles Ordinarires (EDOs)
- Crank-Nicolson 2(3) — Crank-Nicolson est un solveur numérique basé sur le schéma Runge-Kutta fournissant une méthode implicite efficace et stable pour résoudre des Problèmes à Valeur Initiale d'Equations Différentielles Ordinaires (EDOs). Appelé par xcos.
- DDaskr — "Double-precision Differential Algebraic equations system Solver with Krylov method and Rootfinding" : solveur numérique fournissant une méthode efficace et stable pour résoudre des Problèmes à Valeur Initiale d'Equations Différentielles Algebriques (EDAs).
- Comparaisons — Cette page compare les solveurs pour déterminer lequel est le mieux adapté au le problème étudié.
- ode — solveur d'équations différentielles ordinaires
- ode_discrete — ordinary differential equation solver, discrete time simulation
- ode_root — ordinary differential equation solver with roots finding
- odedc — discrete/continuous ode solver
- impl — differential algebraic equation
Bibliographie
ACM SIGNUM Newsletter, Volume 15, Parution 4, Décembre 1980, Pages 10-11 LSode - LSodi
Historique
| Version | Description |
| 5.4.1 | LSodar ajouté |
| Report an issue | ||
| << Solveurs | Solveurs | CVode >> |