Please note that the recommended version of Scilab is 2026.0.0. This page might be outdated.
See the recommended documentation of this function
lqr
LQ compensator (full state)
Syntax
[K, X] = lqr(P12) [K, X] = lqr(P, Q, R) [K, X] = lqr(P, Q, R, S)
Arguments
- P12
A state space representation of a linear dynamical system (see syslin)
- P
A state space representation of a linear dynamical system (see syslin)
- Q
Real symmetric matrix, with same dimensions as P.A
- R
full rank real symmetric matrix
- S
real matrix, the default value is
zeros(size(R,1),size(Q,2))- K
a real matrix, the optimal gain
- X
a real symmetric matrix, the stabilizing solution of the Riccati equation
Description
- Syntax
[K,X]=lqr(P) Computes the linear optimal LQ full-state gain K for the state space representation P
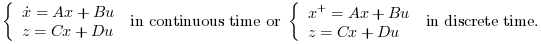 And instantaneous cost function in l2-norm:
And instantaneous cost function in l2-norm:
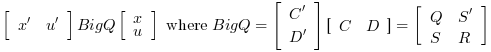
- Syntax
[K,X]=lqr(P,Q,R [,S]) Computes the linear optimal LQ full-state gain K for the linear dynamical system P:
 And instantaneous cost function in l2-norm:
And instantaneous cost function in l2-norm:
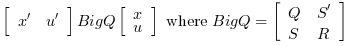
 In this case the P.C and P.D components of the system are ignored.
In this case the P.C and P.D components of the system are ignored.
Algorithm
For a continuous plant, if X is the stabilizing solution of the Riccati equation:
(A - B.R-1.S)'.X + X.(A - B.R-1.S) - X.B.R-1.B'.X + Q - S'.R-1.S = 0
the linear optimal LQ full-state gain K is given by
K = -R-1(B'X + S')
For a discrete plant, if X is the stabilizing solution of the Riccati equation:
A'.X.A - X - (A'.X.B + S')(B'.X.B + R)+(B'.X.A + S) + Q = 0
the linear optimal LQ full-state gain K is given by
K = -(B'.X.B + R)+(B'.X.A + S)
An equivalent form for the equation is
with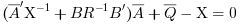
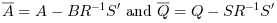
The gain K is such that A + B.K is stable.
The resolution of the Riccati equation is obtained by schur factorization of the 3-blocks matrix pencils associated with these Riccati equations:
For a continuous plant

For a discrete time plant
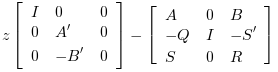
 | It is assumed that matrix R or D'D is non singular. |
 |
Examples
Assume the dynamical system formed by two masses connected by a spring and a damper:
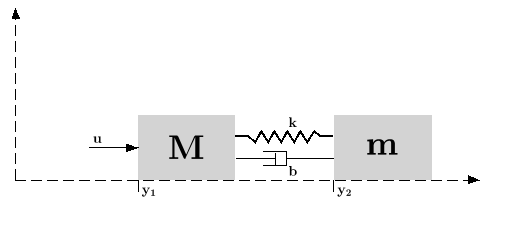
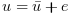 (where e
is a noise) is applied to the big one. Here it is assumed
that the deviations from equilibrium positions of the mass
dy1 and
dy2
positions has well as their derivatives are measured.
(where e
is a noise) is applied to the big one. Here it is assumed
that the deviations from equilibrium positions of the mass
dy1 and
dy2
positions has well as their derivatives are measured.
A state space representation of this system is:
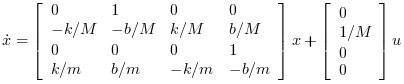
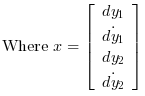
The LQ cost is defined by
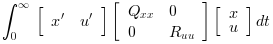
The following instructions may be used to compute a LQ compensator of this dynamical system.
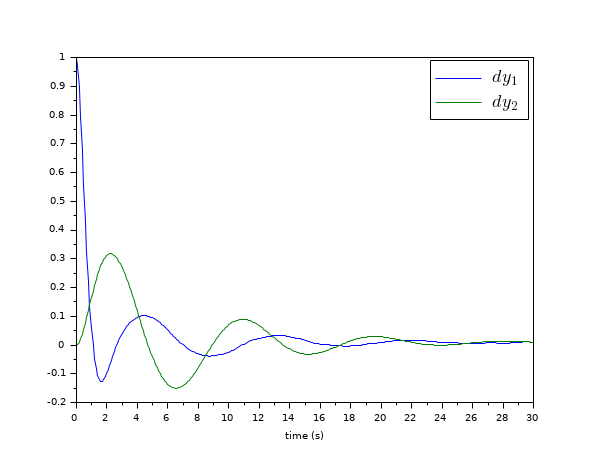
// Form the state space model (assume full state output) M = 1; m = 0.2; k = 0.1; b = 0.004; A = [ 0 1 0 0 -k/M -b/M k/M b/M 0 0 0 1 k/m b/m -k/m -b/m]; B = [0; 1/M; 0; 0]; C = eye(4,4); P = syslin("c",A, B, C); //The compensator weights Q_xx=diag([15 0 3 0]); //Weights on states R_uu = 0.5; //Weight on input Kc=lqr(P,Q_xx,R_uu); //form the Plant+compensator system C=[1 0 0 0 //dy1 0 0 1 0];//dy2 S=C*(P/.(-Kc)); //check system stability and(real(spec(S.A))<0) // Check by simulation dt=0.1; t=0:dt:30; u=0.1*rand(t); y=csim(u,t,S,[1;0;0;0]); clf;plot(t',y');xlabel(_("time (s)")) L=legend(["$dy_1$","$dy_2$"]);L.font_size=4;
Reference
Engineering and Scientific Computing with Scilab, Claude Gomez and al.,Springer Science+Business Media, LLC,1999, ISNB:978-1-4612-7204-5
See also
- lqg — LQG compensator
- lqe — linear quadratic estimator (Kalman Filter)
- gcare — Continuous time control Riccati equation
- leqr — H-infinity LQ gain (full state)
- riccati — Solves the matricial Riccati equation (continuous | discrete time domain)
- schur — [ordered] Schur decomposition of matrix and pencils
| Report an issue | ||
| << lqi | Linear Quadratic | Pole Placement >> |