Please note that the recommended version of Scilab is 2026.0.1. This page might be outdated.
See the recommended documentation of this function
blockdiag
Creates a block diagonal matrix from provided arrays. Block diagonal system connection.
Syntax
r = blockdiag(a1,a2,...,an)
Arguments
- ai
Matrices of booleans, numbers, polynomials, rationals, or strings, of any size. Sparse matrices are accepted.
subsystems (i.e. gains, or linear systems in state-space or transfer form).
- r
Matrix with a1, a2, a3, ... on the diagonal.
ris sparse when at least one of theaiinputs is sparse.
Description
Given the inputs A, B and C,
the output will have these matrices arranged on the diagonal:
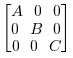 .
.
If all the input matrices are square, the output is known as a block diagonal matrix.
If sub-systems are provided, blockdiag(..) provides the
block-diagonal system made with subsystems put in the main diagonal.
This can be used in particular for system interconnections.
 | blockdiag() can be overloaded. |
Examples
With numbers:
A = [1 0 ; 0 1] B = [3 4 5 ; 6 7 8] C = 7 D = blockdiag(A, B, C)
--> D = blockdiag(A, B, C) D = 1. 0. 0. 0. 0. 0. 0. 1. 0. 0. 0. 0. 0. 0. 3. 4. 5. 0. 0. 0. 6. 7. 8. 0. 0. 0. 0. 0. 0. 7.
With booleans:
blockdiag([%T %T %T], [%T ; %F], [%T %F])
--> blockdiag([%T %T %T], [%T ; %F], [%T %F]) ans = T T T F F F F F F T F F F F F F F F F F F F T F
With polynomials:
s = %s; blockdiag(s, [s^2 ; s^3], [1+s, 1-s^2 ; 4 s^4])
--> b = blockdiag(s, [s^2 ; s^3], [1+s, 1-s^2 ; 4 s^4])
b =
s 0 0 0
2
0 s 0 0
3
0 s 0 0
2
0 0 1 +s 1 -s
4
0 0 4 s
With rationals:
s = %s; blockdiag([1/s 2*s/(4*s+3)], 1/(s-1)^2)
--> blockdiag([1/s 2*s/(4*s+3)], 1/(s-1)^2)
ans =
1 2s 0
-- ------- --
s 3 + 4s 1
0 0 1
-- -- -----------
2
1 1 1 - 2s + s
With some sparse input:
--> S = blockdiag([1 2], sparse([0 3 ; 4 0]), 5) S = ( 4, 5) sparse matrix ( 1, 1) 1. ( 1, 2) 2. ( 2, 4) 3. ( 3, 3) 4. ( 4, 5) 5. --> full(S) ans = 1. 2. 0. 0. 0. 0. 0. 0. 3. 0. 0. 0. 4. 0. 0. 0. 0. 0. 0. 5.
With some text:
blockdiag(["Scilab" "is"],"a",["scientific" ; "software"])
--> blockdiag(["Scilab" "is"], "a", ["scientific" ; "software"]) ans = !Scilab is ! ! a ! ! scientific ! ! software !
With mixed concatenable data types (see the page of brackets []):
blockdiag([%T %F], [-1 3], (1-%z)^2)
--> blockdiag([%T %F], [-1 3], (1-%z)^2)
ans =
1 0 0 0 0
0 0 -1 3 0
2
0 0 0 0 1 -2z +z
With some linear system:
See also
History
| Version | Description |
| 6.1.0 | blockdiag() introduced. |
| Report an issue | ||
| << random | Matrix generation | diag >> |