- Ajuda do Scilab
- Biblioteca de Gráficos
- 2d_plot
- champ
- champ1
- champ_properties
- comet
- contour2d
- contour2di
- contour2dm
- contourf
- errbar
- fchamp
- fec
- fec properties
- fgrayplot
- fplot2d
- grayplot
- grayplot_properties
- graypolarplot
- histplot
- LineSpec
- Matplot
- Matplot1
- Matplot properties
- paramfplot2d
- plot
- plot2d
- plot2d2
- plot2d3
- plot2d4
- polarplot
- scatter
- Sfgrayplot
- Sgrayplot
Please note that the recommended version of Scilab is 2026.0.1. This page might be outdated.
See the recommended documentation of this function
Sfgrayplot
esboço 2d suave de uma superfície definida por uma função utilizando cores
Seqüência de Chamamento
Sfgrayplot(x,y,f,<opt_args>) Sfgrayplot(x,y,f [,strf, rect, nax, zminmax, colminmax, mesh, colout])
Parâmetros
- x,y
vetores linhas de reais de tamanhos n1 e n2.
- f
função do Scilab (z=f(x,y))
- <opt_args>
representa uma seqüência de declarações
key1=value1, key2=value2,... ondekey1,key2,...podem ser um dos seguintes: strf, rect, nax, zminmax, colminmax, mesh, colout (ver plot2d para os três primeiros e fec para os quatro últimos).- strf,rect,nax
ver plot2d.
- zminmax, colminmax, mesh, colout
ver fec.
Descrição
Sfgrayplot é o mesmo que
fgrayplot mas o esboço é suavizado. A função
fec é utilizada para suavização. A superfície é
esboçada assumindo-se que é linear em um conjunto de triângulos
construídos a partir do grid (aqui, com n1=5, n2=3):
_____________ | /| /| /| /| |/_|/_|/_|/_| | /| /| /| /| |/_|/_|/_|/_|
A função colorbar pode ser utilizada para se visualizar a escala de cores (mas você deve saber (ou computar) os valores mínimo e máximo).
Ao invés de Sfgrayplot, você pode usar Sgrayplot este pode ser um pouco mais rápido.
Entre com o comando Sfgrayplot() para visualizar
uma demonstração.
Exemplos
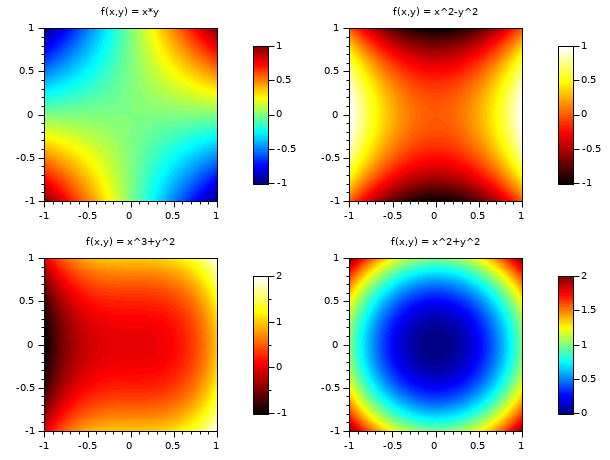
// exemplo #1: esboço de 4 superfícies function z=surf1(x, y), z=x*y, endfunction function z=surf2(x, y), z=x^2-y^2, endfunction function z=surf3(x, y), z=x^3+y^2, endfunction function z=surf4(x, y), z=x^2+y^2, endfunction clf() set(gcf(),"color_map",[jetcolormap(64);hotcolormap(64)]) x = linspace(-1,1,60); y = linspace(-1,1,60); drawlater(); subplot(2,2,1) colorbar(-1,1,[1,64]) Sfgrayplot(x,y,surf1,strf="041",colminmax=[1,64]) xtitle("f(x,y) = x*y") subplot(2,2,2) colorbar(-1,1,[65,128]) Sfgrayplot(x,y,surf2,strf="041",colminmax=[65,128]) xtitle("f(x,y) = x^2-y^2") subplot(2,2,3) colorbar(-1,2,[65,128]) Sfgrayplot(x,y,surf3,strf="041",colminmax=[65,128]) xtitle("f(x,y) = x^3+y^2") subplot(2,2,4) colorbar(0,2,[1,64]) Sfgrayplot(x,y,surf4,strf="041",colminmax=[1,64]) xtitle("f(x,y) = x^2+y^2") drawnow(); show_window()
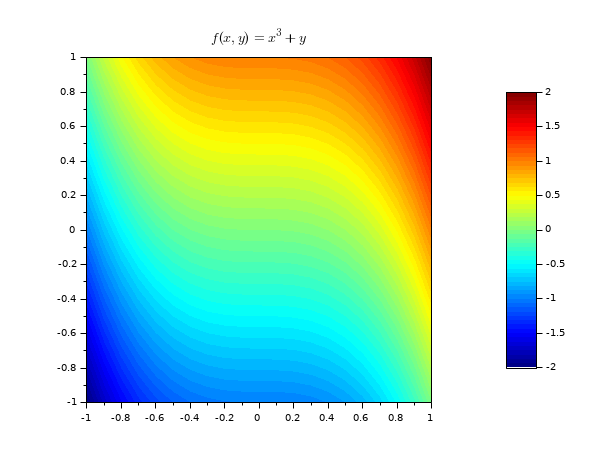
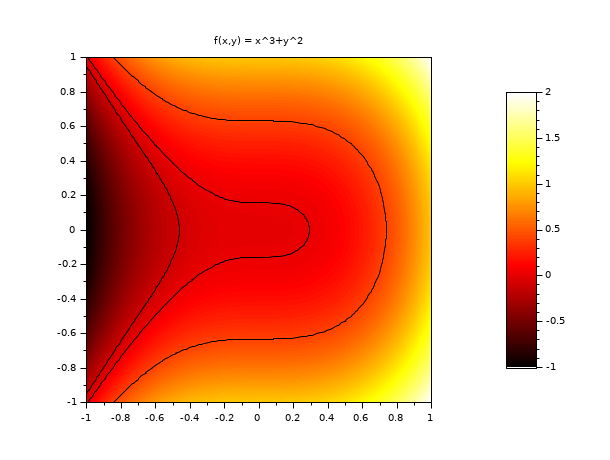
// exemplo #2: esboço de surf3 e adição de algumas linhas de contorno function z=surf3(x, y), z=x^3+y^2, endfunction clf() x = linspace(-1,1,60); y = linspace(-1,1,60); set(gcf(),"color_map",hotcolormap(128)) drawlater(); colorbar(-1,2) Sfgrayplot(x,y,surf3,strf="041") contour2d(x,y,surf3,[-0.1, 0.025, 0.4],style=[1 1 1],strf="000") xtitle("f(x,y) = x^3+y^2") drawnow(); show_window()
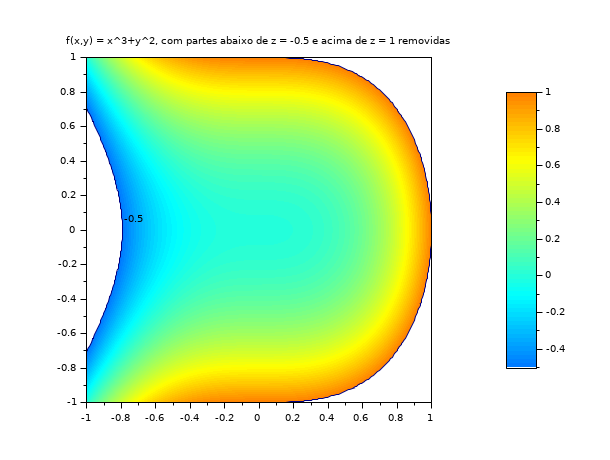
// exemplo #3: esboço de surf3 e uso dos argumentos opcionais zminmax e colout // para restringir o esboço em -0.5<= z <= 1 function z=surf3(x, y), z=x^3+y^2, endfunction clf() x = linspace(-1,1,60); y = linspace(-1,1,60); set(gcf(),"color_map",jetcolormap(128)) drawlater(); zminmax = [-0.5 1]; colors=[32 96]; colorbar(zminmax(1),zminmax(2),colors) Sfgrayplot(x, y, surf3, strf="041", zminmax=zminmax, colout=[0 0], colminmax=colors) contour2d(x,y,surf3,[-0.5, 1],style=[1 1 1],strf="000") xtitle("f(x,y) = x^3+y^2, com partes abaixo de z = -0.5 e acima de z = 1 removidas") drawnow(); show_window()
Ver Também
| Report an issue | ||
| << scatter | 2d_plot | Sgrayplot >> |