Please note that the recommended version of Scilab is 2026.0.1. This page might be outdated.
See the recommended documentation of this function
fft
高速フーリエ変換
ifft
高速フーリエ逆変換
呼び出し手順
X=fft(A [,sign] [,option]) X=fft(A,sign,selection [,option]) X=fft(A,sign,dims,incr [,option] )
パラメータ
- A
実数または複素数ベクトル, 実数または複素数配列(ベクトル, 行列またはN-D配列).
- X
Aと同じ形状の実数または複素数配列- sign
- an integer. with possible values
1or-1. Select direct or inverse transform. The default value is-1(direct transform). - option
- 文字列. 指定可能な値は
"symmetric"または"nonsymmetric"です.Aが対称かどうかを示します. この引数が省略された場合,アルゴリズムはAが対称かどうかを自動的に定義します. 詳細は説明のパートを参照ください. - selection
A配列の次元の添字を有するベクトル. 詳細は説明のパートを参照ください.- dims
- 整数値を有する正の数のベクトルまたは正の整数値のベクトル.
詳細は説明のパートを参照ください.
各要素は
Aの要素の総数の約数とする 必要があります.要素の積は
Aの全要素数より 少ない必要があります. - incr
- 整数値を有する正の数のベクトルまたは正の整数値のベクトル.
詳細は説明のパートを参照ください.
incrは,dimsと同じ要素数とする必要があります.各要素は
Aの全要素数の約数とする必要があります.incr要素は厳密に昇順とする必要があります.
説明
この関数は直接または逆の1次元またはN次元離散フーリエ変換を 行います.- 短縮構文
- 直接
X=fft(A,-1 [,option])またはX=fft(A [,option])は直接変換を出力します.- 単一変量
Aが単一変量のベクトルの場合, 次のように直接FFTが計算されます: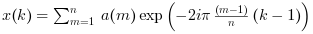
(引数
-1は指数の符号を示しており, "逆"ではありません),- 多変量
Aが行列または多次元配列の場合, 多変量直接FFTが行われます.
- 逆
X=fft(A,1)またはX=ifft(A)は,A==ifft(fft(A))のような 正規化された逆変換を実行します.- 単一変量
Aがベクトルの場合, 単一変量逆FFTが実行されます.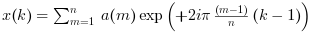
- 多変量
Aが行列または多次元配列の場合, 多変量逆FFTが実行されます.
- 多次元FFTの長い構文
X=fft(A,sign,selection [,option])により,選択した次元方向のAの "スライス"の直接または逆fftを効率的に実行することができます.例えば,
Aが3次元配列の場合,X=fft(A,-1,2)は以下と等価です:X=fft(A,-1,[1 3])は以下と等価です:前記の構文,
X=fft(A,sign,dims,incr [,option])は, 指定した次元方向にAのスライスの 直接または逆fftを行うことも可能です.例えば,
Aがn1*n2*n3個の要素を有する配列の場合,X=fft(A,-1,n1,1)はX=fft(matrix(A,[n1,n2,n3]),-1,1)と等価です. また、X=fft(A,-1,[n1 n3],[1 n1*n2])はX=fft(matrix(A,[n1,n2,n3]),-1,[1,3])と等価です.
- option引数の使用法
この引数は
Aまたはその"スライス"全体 の対称性に関してfftアルゴリズムに情報を提供するために使用できます. 次元n1, ...,npの N次元配列Bは,B==conj(B([1 n1:-1:2],[1 n2:-1:2],...,[1 np:-1:2]))の場合に限り,fftが共役対称です. このような場合, 結果Xは実数で,効率的な専用のアルゴリズムを 使用できます. - "symmetric" は,
Aまたはその全"スライス"を 共役対称として扱うfftを実行する値です. このオプションは,Aまたはその全"スライス" が 丸め誤差の影響で厳密に対称ではない場合に, 自動的な対称性の定義を回避したい場合に有用です. - "nonsymmetric" は対称性を考慮せずに fftを実行する値です. このオプションは自動的な対称性の定義を 回避したい場合に有用です.
- unspecified このオプションが省略された場合,fftアルゴリズムは 自動的に正しい対称性を確認します.
- "symmetric" は,
- fftの最適化
注意: fftw 関数は自動的に直近のパラメータをメモリに保存し, 2回目に再利用します. これにより,(同じパラメータで)連続的なコールを行った場合に 著しく計算時間が改善します.
get_fftw_wisdom, set_fftw_wisdom関数により 更にfftを最適化することができます.
アルゴリズム
この関数は,fftw3 ライブラリを 使用しています.
例
1次元fft
//Frequency components of a signal //---------------------------------- // build a noised signal sampled at 1000hz containing pure frequencies // at 50 and 70 Hz sample_rate=1000; t = 0:1/sample_rate:0.6; N=size(t,'*'); //number of samples s=sin(2*%pi*50*t)+sin(2*%pi*70*t+%pi/4)+grand(1,N,'nor',0,1); y=fft(s); //s is real so the fft response is conjugate symmetric and we retain only the first N/2 points f=sample_rate*(0:(N/2))/N; //associated frequency vector n=size(f,'*') clf() plot(f,abs(y(1:n)))
2次元fft
//---------------------------------- A = zeros(256,256); A(5:24,13:17) = 1; X = fftshift(fft(A)); set(gcf(),"color_map",jetcolormap(128)); clf;grayplot(0:255,0:255,abs(X)')
mupliple fft
//simple case, 3 1-D fft at a time N=2048; t=linspace(0,10,2048); A=[2*sin(2*%pi*3*t)+ sin(2*%pi*3.5*t) 10*sin(2*%pi*8*t) sin(2*%pi*0.5*t)+4*sin(2*%pi*0.8*t)]; X=fft(A,-1,2); fs=1/(t(2)-t(1)); f=fs*(0:(N/2))/N; //associated frequency vector clf;plot(f(1:100)',abs(X(:,1:100))') legend(["3 and 3.5 Hz","8 Hz","0.5 and 0.8 Hz"],"in_upper_left") // 45 3-D fft at a time Dims=[5 4 9 5 6]; A=matrix(rand(1,prod(Dims)),Dims); y=fft(A,-1,[2 4 5]); //equivalent (but less efficient code) y1=zeros(A); for i1=1:Dims(1) for i3=1:Dims(3) ind=list(i1,:,i3,:,:); y1(ind(:))=fft(A(ind(:)),-1); end end
//Using explicit formula for 1-D discrete Fourier transform //------------------------------------------------ function xf=DFT(x, flag); n=size(x,'*'); //Compute the n by n Fourier matrix if flag==1 then,//backward transformation am=exp(2*%pi*%i*(0:n-1)'*(0:n-1)/n); else //forward transformation am=exp(-2*%pi*%i*(0:n-1)'*(0:n-1)/n); end xf=am*matrix(x,n,1);//dft xf=matrix(xf,size(x));//reshape if flag==1 then,xf=xf/n;end endfunction //Comparison with the fast Fourier algorithm a=rand(1,1000); norm(DFT(a,1) - fft(a,1)) norm(DFT(a,-1) - fft(a,-1)) timer();DFT(a,-1);timer() timer();fft(a,-1);timer()
参照
- corr — 相関 , 共分散
- fftw_flags — fftプランナアルゴリズム選択用手法を設定する
- get_fftw_wisdom — fftw wisdomを返す
- set_fftw_wisdom — fftw wisdomを設定
- fftw_forget_wisdom — fftw wisdomをリセット
参考文献
Matteo Frigo and Steven G. Johnson, "FFTW Documentation" http://www.fftw.org/#documentation
| Report an issue | ||
| << dst | Transforms | fft2 >> |