sysdiag

Description

Returns the block-diagonal system made with subsystems put in the main diagonal

ai

subsystems (i.e. gains, or linear systems in state-space or transfer form)

constant, boolean, polynomial or rational matrices of any size

r

a matrix with a1, a2, a3, ... on the diagonal

Description

Given the inputs A, B and C, the output will have these matrices arranged on the diagonal: .

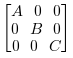If all the input matrices are square, the output is known as a block diagonal matrix.

Used in particular for system interconnections.

Beside this function, you can also use sparse() primitive to build a block diagonal sparse matrix.

For boolean matrices sysdiag() always returns a zero one matrix in the corresponding block ("true" values are replaced by 1 and "false" value by 0).

sysdiag() cannot be used to arrange matrices made of character strings, but you can overload it (see: overloading).

Remark

At most 17 arguments.

Examples

s=poly(0,'s')
sysdiag(rand(2,2),1/(s+1),[1/(s-1);1/((s-2)*(s-3))])
sysdiag(tf2ss(1/s),1/(s+1),[1/(s-1);1/((s-2)*(s-3))])

// a matrix of doubles:
A=[1 0; 0 1], B=[3 4 5; 6 7 8], C=7
D=sysdiag(A,B,C)
//
sysdiag([%t %f; %f %t], eye(2,2), ones(3,3))
// a polynomial matrix:
s=%s;
sysdiag([s 4*s; 4 s^4], [1 s^2 s+2; 3*s 2 s^2-1])
// a rational matrix:
sysdiag([1/s 2*s/(4*s+3)], [s; 4; 1/(s^2+2*s+1)])
// a block diagonal sparse matrix:
S=sysdiag([1 2; 3 4], [5 6; 7 8], [9 10; 11 12], [13 14; 15 16])
S=sparse(S)

See also

• brackets — Concaténation. Récipients d'une affectation. Résultats d'une function
• insertion — insertion/modification dans une variable
• feedback — feedback operation
• diag — extraction de diagonale ou construction d'une matrice avec un vecteur en diagonal
• bdiag — bloc-diagonalisation, vecteurs propres généralisés
• sparse — sparse matrix definition
• repmat — Définit un grand tableau par pavage avec un tableau 2D.