atan

Аргументы

x

вещественный или комплексный скаляр, вектор или матрица

phi

вещественный или комплексный скаляр, вектор или матрица

x, y

вещественные скаляры, векторы или матрицы одинаковых размеров

phi

вещественный скаляр, вектор или матрица

Описание

Первая форма вычисляет 2-х квадрантный арктангенс, который является обратным значением от tan(phi). Для вещественного x, phi лежит на интервале 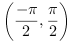. Для комплексного x, atan имеет две неопределённые точки, точки перехода +%i, -%i и выбираемые переходы являются двумя мнимыми полупрямыми линиям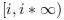и и .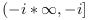

Вторая форма вычисляет 4-х квадрантный арктангенс (в Фортране atan2), то есть она возвращает аргумент (угол) комплексного числа x+i*y. Диапазон atan(y, x) равен .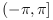

Для вещественных аргументов обе формы дают идентичные значения, если x>0.

Если аргумент является вектором или матрицей, то вычисление выполняется поэлементно, так что phi является вектором или матрицей того же размера, при этом phi(i, j) = atan(x(i, j)) или phi(i, j) = atan(y(i, j), x(i, j)).

Примеры

// примеры со второй формой
x=[1,%i,-1,%i]
phase_x = atan(imag(x),real(x))
atan(0,-1)
atan(-%eps,-1)

// переходы
atan(-%eps + 2*%i)
atan(+%eps + 2*%i)
atan(-%eps - 2*%i)
atan(+%eps - 2*%i)

// значения в точках перехода
ieee(2)
atan(%i)
atan(-%i)

Смотрите также

• tan — тангенс
• unwrap — unwrap a Y(x) profile or a Z(x,y) surface. Unfold a Y(x) profile
• ieee — установка режима исключения с плавающей запятой