Please note that the recommended version of Scilab is 2026.0.1. This page might be outdated.
See the recommended documentation of this function
ndgrid
construit des matrices ou hypermatrices en répliquant des vecteurs
Séquences d'appel
[X, Y] = ndgrid(x) [X, Y] = ndgrid(x,y) [X, Y, Z] = ndgrid(x,y,z) [X, Y, Z, T] = ndgrid(x,y,z,t) [X1, X2, ..., Xm] = ndgrid(x1,x2,...,xm)
Paramètres
- x, y, z, ...
vecteurs de types simples quelconques possiblement distincts (booléens, entiers encodés, décimaux, complexes, polynômes, rationnels, textes). Par défaut,
y=x.- X, Y, Z, ...
Matrices (si seulement 2 vecteurs d'entrée), ou hypermatrices, toutes de tailles identiques : size(x,"*") lignes, size(y,"*") colonnes, size(z,"*") feuilles, etc.
Par ailleurs,
Xa le type dex;Ya le type dey; etc.
Description
La première application de ndgrid consiste à
construire une grille multidimensionnelle de noeuds échantillonnant
l'espace 2D ou 3D ou N-D, à partir de 2, 3 ou N vecteurs
x, y, etc.. indiquant
l'échantillonage de chaque direction de l'espace.
Pour ce faire,
- la matrice ou l'hypermatrice
Xest construite en répliquant le vecteurxdans toutes ses colonnes ; - la matrice ou l'hypermatrice
Yest construite en répliquant le vecteurydans toutes ses lignes ; - la matrice ou l'hypermatrice
Zest construite en répliquant le vecteurzen épaisseur pour tous les points (x,y) ; etc.
--> [X, Y] = ndgrid([1 3 4], [0 2 4 6])
X =
1. 1. 1. 1.
3. 3. 3. 3.
4. 4. 4. 4.
Y =
0. 2. 4. 6.
0. 2. 4. 6.
0. 2. 4. 6.
Les coordonnées du noeud node(i,j) dans l'espace 2D seront alors
simplement [x(i), y(j)] maintenant données par
[X(i,j), Y(i,j)]. De même, les coordonnées du noeud
node(i,j,k) dans une grille 3D seront
[x(i), y(j), z(k)] données par
[X(i,j,k), Y(i,j,k), Z(i,j,k)].
Ce schéma de construction par réplication peut être utilisé pour construire une grille à un nombre N quelconque de dimensions. Par ailleurs, il est indépendant de la nature des vecteurs de base répliqués et peut donc être utilisé pour tous les types de données uniformes. A titre d'exemple, considérons un ensemble d'objets ayant tous 2 attributs :
- Le premier est un nombre
n, avec 2 valeurs possibles, par exemple:n = [ 3 7 ] - Le second est une lettre, avec 6 choix possibles,
par exemple:
c = ["a" "e" "i" "o" "u" "y"]
objets :
--> [N, C] = ndgrid([3 7],["a" "e" "i" "o" "u" "y"]) C = !a e i o u y ! !a e i o u y ! N = 3. 3. 3. 3. 3. 3. 7. 7. 7. 7. 7. 7.
De là, l'objet(i,j) aura les attributs
{n(i) c(j)} que l'on pourra maintenant désigner par
{N(i,j) C(i,j)}.
Ce type de grille pourra être utilisée pour initialiser un tableau
2D de structures ayant 2 champs n et c.
Les exemples suivants montrent comment utiliser les matrices ou
hypermatrices X, Y, Z produites, pour des applications
usuelles.
Exemples
Exemple #1:
// Créons une grille de points {X,Y} x = linspace(-10,2,40); y = linspace(-5,5,40); [X,Y] = ndgrid(x,y); // x et y sont répliqués pour créer la grille // Calculons des ordonnées Z(X,Y) et traçons Z(X,Y) : Z = X - 3*X.*sin(X).*cos(Y-4) ; clf() plot3d(x,y,Z, flag=[color("green") 2 4], alpha=7, theta=60); show_window()
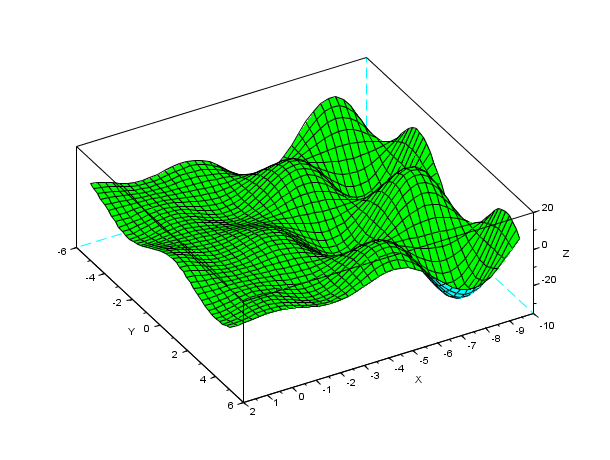
Exemple #2:
// Créons une grille en 3 dimensions nx = 10; ny = 6; nz = 4; x = linspace(0,2,nx); y = linspace(0,1,ny); z = linspace(0,0.5,nz); [X,Y,Z] = ndgrid(x,y,z); // Nous choisissons ici une représentation cartésienne, mais l'on pourrait // aussi travailler en coordonnées cylindriques, sphériques, ou autres. // Transformons les coordonnées pour plot3d() : XF=[]; YF=[]; ZF=[]; for k=1:nz [xf,yf,zf] = nf3d(X(:,:,k),Y(:,:,k),Z(:,:,k)); XF = [XF xf]; YF = [YF yf]; ZF = [ZF zf]; end for j=1:ny [xf,yf,zf] = nf3d(matrix(X(:,j,:),[nx,nz]),... matrix(Y(:,j,:),[nx,nz]),... matrix(Z(:,j,:),[nx,nz])); XF = [XF xf]; YF = [YF yf]; ZF = [ZF zf]; end // Affichage : clf() plot3d(XF,YF,ZF, flag=[0 6 3], 66, 61, leg="X@Y@Z") xtitle("A 3d grid !"); show_window()
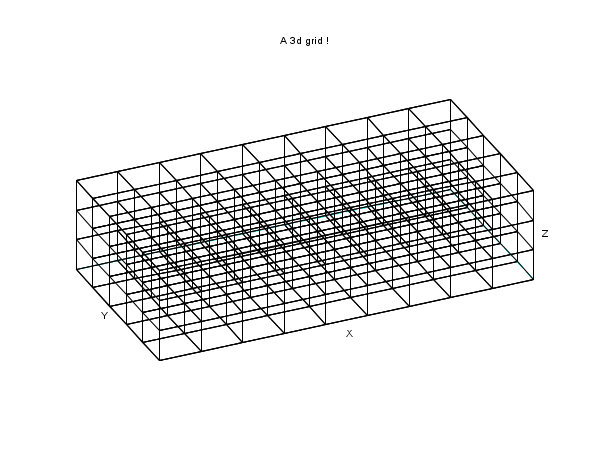
Exemple #3: création d'une table de digrammes
[c1, c2] = ndgrid(["a" "b" "c"], ["a" "b" "c" "d" "e" "f" "g" "h"]) c1+c2
--> [c1, c2] = ndgrid(["a" "b" "c"], ["a" "b" "c" "d" "e" "f" "g" "h"]) c2 = !a b c d e f g h ! !a b c d e f g h ! !a b c d e f g h ! c1 = !a a a a a a a a ! !b b b b b b b b ! !c c c c c c c c ! --> c1+c2 ans = !aa ab ac ad ae af ag ah ! !ba bb bc bd be bf bg bh ! !ca cb cc cd ce cf cg ch !
Voir aussi
Historique
| Version | Description |
| 6.0.0 | Extension à tous les types de données uniformes ([], booléens, entiers encodés, polynomes, fractions rationelles, texte). Révision de la page d'aide. |
| 6.0.1 | ndgrid(x) est désormais accepté (y=x). |
| Report an issue | ||
| << meshgrid | Matrice - génération | ones >> |