Please note that the recommended version of Scilab is 2026.0.1. This page might be outdated.
See the recommended documentation of this function
ss2zp
SIMO state space system to zero pole gain representation
Syntax
[z,p,k]=ss2zp(S)
Arguments
- S
a single input linear system in state space representation.
- z
a matrix, the ith column contains the transmission zeros relative to the ith output.
- p
a column vector, the poles of the system
- k
a column vector, the ith element contains the gain relative to the ith output.
Description
Converts a SIMO state space system into zero pole gain representation.
The zeros and gain are computed using the upper triangular
Kronecker form (see kroneck)
of the matrix pencil
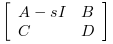
Examples
References
A. Emami-Naeini, P. Van Dooren "CComputation of zeros of linear multivariable systems" Automatica. Vol. 18, 1982, p. 415
See Also
History
| Версия | Описание |
| 6.0 | Function added. |
| Report an issue | ||
| << ss2tf | Linear System Representation | ssprint >> |