- Aide de Scilab
- Fonctions Elémentaires
- Trigonométrie
- acos
- acosd
- acosh
- acoshm
- acosm
- acoth
- asec
- asecd
- asech
- asin
- asind
- asinh
- asinhm
- asinm
- atand
- atanhm
- atanm
- cos
- cosd
- cosh
- coshm
- cosm
- cotd
- cotg
- coth
- cothm
- csc
- cscd
- sec
- secd
- sech
- sin
- sind
- sinh
- sinhm
- sinm
- tan
- tanh
- tanhm
- tanm
- acot
- acotd
- acsc
- acscd
- acsch
- atan
- atanh
- csch
- csgn
- sinc
- tand
Please note that the recommended version of Scilab is 2026.0.1. This page might be outdated.
See the recommended documentation of this function
atan
2-quadrant and 4-quadrant inverse tangent
Calling Sequence
phi = atan(x) phi = atan(y, x)
Arguments
- x
a real or complex scalar, vector or matrix.
- phi
a real or complex scalar, vector or matrix.
- x, y
a real scalars, vectors or matrices of the same size.
- phi
a real scalar, vector or matrix.
Description
The first form computes the 2-quadrant inverse tangent, which is the
inverse of tan(phi). For real x,
phi is in the interval 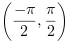 . For complex
. For complex
x, atan has two singular, branching
points +%i, -%i and the chosen branch
cuts are the two imaginary half-straight lines 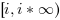 and
and 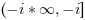 .
.
The second form computes the 4-quadrant arctangent (atan2 in
Fortran), this is, it returns the argument (angle) of the complex number
x+i*y. The range of atan(y, x) is
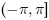 .
.
For real arguments, both forms yield identical values if
x>0.
In case of vector or matrix arguments, the evaluation is done
element-wise, so that phi is a vector or matrix of the
same size with phi(i, j) = atan(x(i, j)) or
phi(i,j) = atan(y(i, j), x(i, j)).
Examples
See Also
| Report an issue | ||
| << acsch | Trigonométrie | atanh >> |