qp_solve

Arguments

Q

real positive definite symmetric matrix (dimension n x n ).

p

real (column) vector (dimension n)

C

real matrix (dimension (me + md) x n). This matrix may be dense or sparse.

b

RHS column vector (dimension m=(me + md) )

me

number of equality constraints (i.e. x'*C(:,1:me) = b(1:me)' )

x

optimal solution found.

iact

vector, indicator of active constraints. The non zero entries give the index of the active constraints. The entries of the iact vector are ordered this way: equality constraints come first, then come the inequality constraints.

iter

2x1 vector, first component gives the number of "main" iterations, the second one says how many constraints were deleted after they became active.

Description

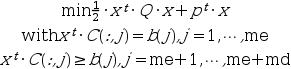
This function requires Q to be symmetric positive definite. If this hypothesis is not satisfied, one may use the contributed quapro toolbox.

Examples

// Find x in R^6 such that:
// x'*C1 = b1 (3 equality constraints i.e me=3)
C1= [ 1,-1, 2;
     -1, 0, 5;
      1,-3, 3;
      0,-4, 0;
      3, 5, 1;
      1, 6, 0];
b1=[1;2;3];

// x'*C2 >= b2 (2 inequality constraints)
C2= [ 0 ,1;
     -1, 0;
      0,-2;
     -1,-1;
     -2,-1;
      1, 0];
b2=[ 1;-2.5];

// and minimize 0.5*x'*Q*x - p'*x with
p=[-1;-2;-3;-4;-5;-6]; Q=eye(6,6);

me=3;
[x,iact,iter,f]=qp_solve(Q,p,[C1 C2],[b1;b2],me)
// Only linear constraints (1 to 4) are active

See Also

• optim
• qld
• qpsolve

The contributed toolbox "quapro" may also be of interest, in particular for singular Q.

Memory requirements

Let r be

r=min(m,n)

Then the memory required by qp_solve during the computations is

2*n+r*(r+5)/2 + 2*m +1

References

• Goldfarb, D. and Idnani, A. (1982). "Dual and Primal-Dual Methods for Solving Strictly Convex Quadratic Programs", in J.P. Hennart (ed.), Numerical Analysis, Proceedings, Cocoyoc, Mexico 1981, Vol. 909 of Lecture Notes in Mathematics, Springer-Verlag, Berlin, pp. 226-239.

• Goldfarb, D. and Idnani, A. (1983). "A numerically stable dual method for solving strictly convex quadratic programs", Mathematical Programming 27: 1-33.

• QuadProg (Quadratic Programming Routines), Berwin A Turlach,http://www.maths.uwa.edu.au/~berwin/software/quadprog.html

Used Functions

qpgen2.f and >qpgen1.f (also named QP.solve.f) developped by Berwin A. Turlach according to the Goldfarb/Idnani algorithm