Please note that the recommended version of Scilab is 2026.0.0. This page might be outdated.
However, this page did not exist in the previous stable version.
derivative
approximate derivatives of a function
Calling Sequence
derivative(F,x) [J [,H]] = derivative(F,x [,h ,order ,H_form ,Q])
Arguments
- F
a Scilab function F:
R^n --> R^mor alist(F,p1,...,pk), where F is a scilab function in the formy=F(x,p1,...,pk), p1, ..., pk being any scilab objects (matrices, lists,...).- x
real column vector of dimension n.
- h
(optional) real, the stepsize used in the finite difference approximations.
- order
(optional) integer, the order of the finite difference formula used to approximate the derivatives (order = 1,2 or 4, default is order=2 ).
- H_form
(optional) string, the form in which the Hessean will be returned. Possible forms are:
- H_form='default'
H is a m x (
n^2) matrix ; in this form, the k-th row of H corresponds to the Hessean of the k-th component of F, given as the following row vector :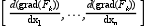
((grad(F_k) being a row vector).
- H_form='blockmat' :
H is a (mxn) x n block matrix : the classic Hessean matrices (of each component of F) are stacked by row (H = [H1 ; H2 ; ... ; Hm] in scilab syntax).
- H_form='hypermat' :
H is a n x n matrix for m=1, and a n x n x m hypermatrix otherwise. H(:,:,k) is the classic Hessean matrix of the k-th component of F.
- Q
(optional) real matrix, orthogonal (default is eye(n,n)). Q is added to have the possibility to remove the arbitrariness of using the canonical basis to approximate the derivatives of a function and it should be an orthogonal matrix. It is not mandatory but better to recover the derivative as you need the inverse matrix (and so simply Q' instead of inv(Q)).
- J
approximated Jacobian
- H
approximated Hessian
Description
Numerical approximation of the first and second derivatives of a
function F: R^n --> R^m at the point x. The
Jacobian is computed by approximating the directional derivatives of the
components of F in the direction of the columns of Q. (For m=1, v=Q(:,k) :
grad(F(x))*v = Dv(F(x)).) The second derivatives are computed by
composition of first order derivatives. If H is given in its default form
the Taylor series of F(x) up to terms of second order is given by :
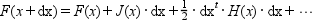
(([J,H]=derivative(F,x,H_form='default'), J=J(x), H=H(x).)
Performances
If the problem is correctly scaled, increasing the accuracy reduces
the total error but requires more function evaluations.
The following list presents the number of function evaluations required to
compute the Jacobian depending on the order of the formula and the dimension of x,
denoted by n:
order=1, the number of function evaluations isn+1,order=2, the number of function evaluations is2n,order=4, the number of function evaluations is4n.
Computing the Hessian matrix requires square the number of function evaluations, as detailed in the following list.
order=1, the number of function evaluations is(n+1)^2,order=2, the number of function evaluations is4n^2,order=4, the number of function evaluations is16n^2.
Remarks
The step size h must be small to get a low error but if it is too small floating point errors will dominate by cancellation. As a rule of thumb, do not change the default step size. To work around numerical difficulties one may also change the order and/or choose different orthogonal matrices Q (the default is eye(n,n)), especially if the approximate derivatives are used in optimization routines. All the optional arguments may also be passed as named arguments, so that one can use calls in the form :
derivative(F, x, H_form = "hypermat") derivative(F, x, order = 4) etc.
Examples
function y=F(x) y=[sin(x(1)*x(2))+exp(x(2)*x(3)+x(1)) ; sum(x.^3)]; endfunction function y=G(x, p) y=[sin(x(1)*x(2)*p)+exp(x(2)*x(3)+x(1)) ; sum(x.^3)]; endfunction x=[1;2;3]; [J,H]=derivative(F,x,H_form='blockmat') n=3; // form an orthogonal matrix : Q = qr(rand(n,n)) // Test order 1, 2 and 4 formulas. for i=[1,2,4] [J,H]=derivative(F,x,order=i,H_form='blockmat',Q=Q); mprintf("order= %d \n",i); H, end p=1; h=1e-3; [J,H]=derivative(list(G,p),x,h,2,H_form='hypermat'); H [J,H]=derivative(list(G,p),x,h,4,Q=Q); H // Taylor series example: dx=1e-3*[1;1;-1]; [J,H]=derivative(F,x); F(x+dx) F(x+dx)-F(x) F(x+dx)-F(x)-J*dx F(x+dx)-F(x)-J*dx-1/2*H*(dx .*. dx) // A trivial example function y=f(x, A, p, w) y=x'*A*x+p'*x+w; endfunction // with Jacobian and Hessean given by J(x)=x'*(A+A')+p', and H(x)=A+A'. A = rand(3,3); p = rand(3,1); w = 1; x = rand(3,1); [J,H]=derivative(list(f,A,p,w),x,h=1,H_form='blockmat') // Since f(x) is quadratic in x, approximate derivatives of order=2 or 4 by finite // differences should be exact for all h~=0. The apparent errors are caused by // cancellation in the floating point operations, so a "big" h is choosen. // Comparison with the exact matrices: Je = x'*(A+A')+p' He = A+A' clean(Je - J) clean(He - H)
Accuracy issues
The derivative function uses the same step h
whatever the direction and whatever the norm of x.
This may lead to a poor scaling with respect to x.
An accurate scaling of the step is not possible without many evaluations
of the function. Still, the user has the possibility to compare the results
produced by the derivative and the numdiff
functions. Indeed, the numdiff function scales the
step depending on the absolute value of x.
This scaling may produce more accurate results, especially if
the magnitude of x is large.
In the following Scilab script, we compute the derivative of an
univariate quadratic function. The exact derivative can be
computed analytically and the relative error is computed.
In this rather extreme case, the derivative function
produces no significant digits, while the numdiff
function produces 6 significant digits.
// Difference between derivative and numdiff when x is large function y=myfunction(x) y = x*x; endfunction x = 1.e100; fe = 2.0 * x; fp = derivative(myfunction,x); e = abs(fp-fe)/fe; mprintf("Relative error with derivative: %e\n",e) fp = numdiff(myfunction,x); e = abs(fp-fe)/fe; mprintf("Relative error with numdiff: %e\n",e)
The previous script produces the following output.
In a practical situation, we may not know what is the correct numerical derivative. Still, we are warned that the numerical derivatives should be used with caution in this specific case.
Authors
Rainer von Seggern, Bruno Pincon
| << datafit | Optimization and Simulation | fit_dat >> |