Please note that the recommended version of Scilab is 2026.0.1. This page might be outdated.
See the recommended documentation of this function
plot3d
esboço 3d de uma superfície
Seqüência de Chamamento
plot3d(x,y,z,[theta,alpha,leg,flag,ebox]) plot3d(x,y,z,<opt_args>) plot3d(xf,yf,zf,[theta,alpha,leg,flag,ebox]) plot3d(xf,yf,zf,<opt_args>) plot3d(xf,yf,list(zf,colors),[theta,alpha,leg,flag,ebox]) plot3d(xf,yf,list(zf,colors),<opt_args>)
Parâmetros
- x,y
vetores linhas de tamanhos n1 e n2 (coordenadas dos eixos x e y). Estas coordenadas devem ser monótonas.
- z
matriz de tamanho (n1,n2).
z(i,j)é o valor da superfície no ponto (x(i),y(j)).- xf,yf,zf
matrizes de tamanho (nf,n). Elas definem as facetas usadas para desenhar a superfície. Há
nfacetas. Cada facetaié definida por um polígono comnfpontos. As coordenadas dos eixos x, y e z dos pontos da i-ésima faceta são dados respectivamente porxf(:,i),yf(:,i)ezf(:,i).- colors
um vetor de tamanho n fornecendo as cores de cada faceta ou uma matriz de tamanho (nf,n) fornecendo a cor próxima a cada borda da faceta (a cor da faceta é interpolada).
- <opt_args>
representa uma seqüência de sentenças
key1=value1, key2=value2,... ondekey1,key2,...pode ser um dos seguintes: theta, alpha , leg, flag, ebox (ver definições abaixo).- theta, alpha
valores reais de dados em graus, as coordenadas esféricas de observação do ponto.
- leg
string definindo os rótulos para cada eixo com @ como um separador de campos, por exemplo "X@Y@Z".
- flag
um vetor real de tamanho três.
flag=[mode,type,box].- mode
um inteiro (cor da superfície).
- mode>0
a superfície é pintada com a cor
"mode"; a borda da faceta é desenhada com o estilo e linha e cor correntes.- mode=0:
uma malha da superfície é desenhada.
- mode<0:
a superfície é pintada com a cor
"-mode"; a borda da faceta não é desenhada.Note que o tratamento de cor da superfície pode ser feito utilizando-se as opções
color_modeecolor_flagatravés das propriedades da entidade superfície (ver surface_properties).
- type
um inteiro (tipo de escala).
- type=0:
o esboço é feito utilizando-se a escala 3d corrente (definida por uma chamada anterior a
param3d,plot3d,contourouplot3d1).- type=1:
re-escala automaticamente caixas 3d com relção de aspecto extrema, as fronteiras são especificadas pelo valor do argumento opcional
ebox.- type=2:
re-escala automaticamente caixas 3d com relção de aspecto extrema, as fronteiras são computadas utilizando-se dados fornecidos.
- type=3:
fronteiras 3d isométricas com fronteiras da caixa dadas por
ebox, de modo semelhante atype=1.- type=4:
fronteiras 3d isométricas derivadas dos dados, de modo semelhante a
type=2.- type=5:
fronteiras 3d isométricas expandidas com fronteiras fornecidas por
ebox, de modo semelhante atype=1.- type=6:
fronteiras 3d isométricas expandidas derivadas dos dados, de modo semelhante a
type=2.Note que as fronteiras dos eixos podem ser customizadas através das propriedades da entidade de eixos (ver axes_properties).
- box
um inteiro (moldura ao redor do esboço).
- box=0:
nada é desenhado ao redor do esboço.
- box=1:
não implementado (é como box=0).
- box=2:
apenas os eixos atrás da superfície são desenhados.
- box=3:
uma caixa cercando a superfície é desenhada e legendas são adicionadas.
- box=4:
uma caixa cercando a superfície é desenhada e legendas e eixos são adicionados.
Note que o aspecto dos eixos pode ser customizado através das propriedades da entidade de eixos (ver axes_properties).
- ebox
especifica as fronteiras do esboço através do vetor
[xmin,xmax,ymin,ymax,zmin,zmax]. Este argumento é utilizado junto comtypeemflag, se este for ajustado para1,3ou5(volte acima para ver o comportamento correspondente). Seflagestiver faltando,eboxnão é levado em conta.Note que, quando especificado, o argumento
eboxage no campodata_boundsque também pode ser ajustado através das propriedades da entidade de eixos (ver axes_properties).
Descrição
plot3d(x,y,z,[theta,alpha,leg,flag,ebox]) desenha
a superfície parametrizada z=f(x,y).
plot3d(xf,yf,zf,[theta,alpha,leg ,flag,ebox])
desenha uma superfície definida por um conjunto de facetas. Você pode
desenhar esboços multiplos substituindo xf,
yf e zf por múltiplas matrizes
montadas por linhas como [xf1 xf2 ...], [yf1
yf2 ...] e [zf1 zf2 ...]. Note que os dados
também podem ser ajustados ou recebidos através das propriedades da
entidade superfície (ver surface_properties).
Você pode fornecer uma cor específica para cada faceta utilizando
list(zf,colors) ao invés de zf, onde
colors é um vetor de tamanho n. Se
colors(i) for positivo, fornece a cor da faceta
i e a borda da faceta é desenhada utilizando-se o
estilo de linha e cor correntes. Se colors(i) for
negativo, o identificador de cor -colors(i) é utilizado
e a borda da faceta não é desenhada.
Também é possível obter cores interpoladas para as facetas. Para
este tipo de cor, o argumento deve ser uma matriz nf x n fornecendo as
cores próximas a cada borda da faceta de cada faceta. Neste caso, valores
positivos para cores significam que as bordas não seram desenhadas. Note
que as cores também podem ser ajustadas através das propriedades da
entidade Surface (superfície) (via tlist affectations)
e editadas utilizando-se a opção color_flag (ver surface_properties).
Os arugumentos opcionais theta, alpha, leg ,flag,
ebox, podem ser passados por uma seqüência de argumentos
key1=value1, key2=value2, ... Neste caso, a ordem não
tem significado especial. Note que todos estes argumentos, exceto
flag podem ser customizados através de propriedades da
entidade de eixos (ver axes_properties). Como descrito
anteriormente, a opção flag lida com as propriedades da
entidade superfície para mode (ver surface_properties) e as propriedades
de eixos (Axes) para type e box (ver
axes_properties).
Você pode utilizar a função genfac3d para
computar facetas de quatro lados da superfície
z=f(x,y). eval3dp também pode ser
utilizado.
Entre com o comando plot3d() para visualizar uma
demonstração.
Exemplos
// esboço simples utilizando z=f(x,y) t=[0:0.3:2*%pi]'; z=sin(t)*cos(t'); plot3d(t,t,z) // o mesmo esboço utilizando facetas computadas por genfac3d [xx,yy,zz]=genfac3d(t,t,z); clf() plot3d(xx,yy,zz) // esboços múltiplos clf() plot3d([xx xx],[yy yy],[zz 4+zz]) // esboços múltiplos utilizando-se cores clf() plot3d([xx xx],[yy yy],list([zz zz+4],[4*ones(1,400) 5*ones(1,400)])) // esboço simples utilizando ponto de observação e legendas clf() plot3d(1:10,1:20,10*rand(10,20),alpha=35,theta=45,flag=[2,2,3]) // esboço de uma esfera utilizando utilizando facetas computadas por eval3dp deff("[x,y,z]=sph(alp,tet)",["x=r*cos(alp).*cos(tet)+orig(1)*ones(tet)";.. "y=r*cos(alp).*sin(tet)+orig(2)*ones(tet)";.. "z=r*sin(alp)+orig(3)*ones(tet)"]); r=1; orig=[0 0 0]; [xx,yy,zz]=eval3dp(sph,linspace(-%pi/2,%pi/2,40),linspace(0,%pi*2,20)); clf();plot3d(xx,yy,zz) clf(); f=gcf(); f.color_map = hotcolormap(128); r=0.3;orig=[1.5 0 0]; [xx1,yy1,zz1]=eval3dp(sph,linspace(-%pi/2,%pi/2,40),linspace(0,%pi*2,20)); cc=(xx+zz+2)*32;cc1=(xx1-orig(1)+zz1/r+2)*32; clf();plot3d1([xx xx1],[yy yy1],list([zz,zz1],[cc cc1]),theta=70,alpha=80,flag=[5,6,3]) //operações disponíveis apenas no novo modo de gráficos delete(gcf()); t=[0:0.3:2*%pi]'; z=sin(t)*cos(t'); [xx,yy,zz]=genfac3d(t,t,z); plot3d([xx xx],[yy yy],list([zz zz+4],[4*ones(1,400) 5*ones(1,400)])) e=gce(); f=e.data; TL = tlist(["3d" "x" "y" "z" "color"],f.x,f.y,f.z,6*rand(f.z)); // matriz de cores aleatória e.data = TL; TL2 = tlist(["3d" "x" "y" "z" "color"],f.x,f.y,f.z,4*rand(1,800)); // vetor de cores aleatório e.data = TL2; TL3 = tlist(["3d" "x" "y" "z" "color"],f.x,f.y,f.z,[20*ones(1,400) 6*ones(1,400)]); e.data = TL3; TL4 = tlist(["3d" "x" "y" "z"],f.x,f.y,f.z); // nenhuma cor e.data = TL4; e.color_flag=1 // índice de cor proporcional à altitude (coordenada z) e.color_flag=2; // de volta ao modo padrão e.color_flag= 3; // modo de gradação interpolada (baseada na cor azul padrão) clf() plot3d([xx xx],[yy yy],list([zz zz+4],[4*ones(1,400) 5*ones(1,400)])) h=gce(); //obtendo manipulador da entidade corrente (aqui é a superfície) a=gca(); //obtendo eixos correntes a.rotation_angles=[40,70]; a.grid=[1 1 1]; //criando grides a.data_bounds=[-6,0,-1;6,6,5]; a.axes_visible="off"; //os eixo estão escondidos a.axes_bounds=[.2 0 1 1]; h.color_flag=1; //colorindo de acordo com z h.color_mode=-2; //removendo as bordas das facetas ajustando color_mode para a cor branca h.color_flag=2; //colorindo de acordo com as cores fornecidas h.color_mode = -1; // colocando de volta as bordas das facetas ajustando color_mode de volta para preto f=gcf();//obtendo o manipulador da figura raiz f.color_map=hotcolormap(512); c=[1:400,1:400]; TL.color = [c;c+1;c+2;c+3]; h.data = TL; h.color_flag=3; // modo de gradação interpolada
We can use the plot3d function to plot a set of patches (triangular, quadrangular, etc).
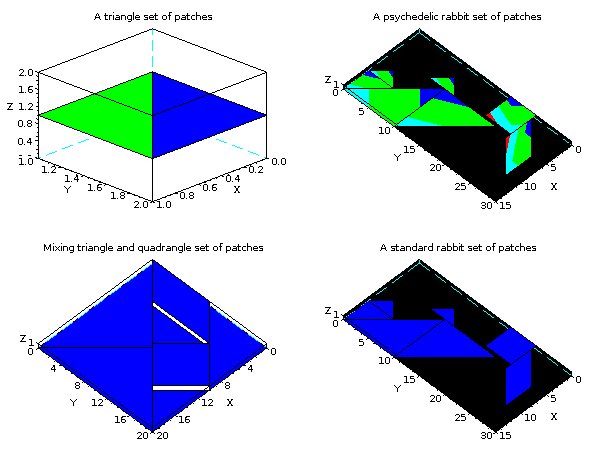
// The plot3d function to draw patches: // patch(x,y,[z]) // patch(x,y,[list(z,c)]) // The size of x : number of points in the patches x number of patches // y and z have the same sizes as x // c: // - a vector of size number of patches: the color of the patches // - a matrix of size number of points in the patches x number of // patches: the color of each points of each patches // Example 1: a set of triangular patches x = [0 0; 0 1; 1 1]; y = [1 1; 2 2; 2 1]; z = [1 1; 1 1; 1 1]; tcolor = [2 3]'; subplot(2,2,1); plot3d(x,y,list(z,tcolor)); xtitle('A triangle set of patches'); // Example 2: a mixture of triangular and quadrangular patches xquad = [5, 0; 10,0; 15,5; 10,5]; yquad = [15,0; 20,10; 15,15; 10,5]; zquad = ones(4,2); xtri = [ 0,10,10, 5, 0; 10,20,20, 5, 0; 20,20,15,10,10]; ytri = [ 0,10,20, 5,10; 10,20,20,15,20; 0, 0,15,10,20]; ztri = zeros(3,5); subplot(2,2,3); plot3d(xquad,yquad,zquad); plot3d(xtri,ytri,ztri); xtitle('Mixing triangle and quadrangle set of patches'); // Example 3: some rabbits rabxtri = [ 5, 5, 2.5, 7.5, 10; 5, 15, 5, 10, 10; 15, 15, 5, 10, 15]; rabytri = [10, 10, 9.5, 2.5, 0; 20, 10, 12, 5, 5; 10 0 7 0 0]; rabztri = [0,0,0,0,0; 0,0,0,0,0; 0,0,0,0,0]; rabtricolor_byface = [2 2 2 2 2]; rabtricolor = [2,2,2,2,2; 3,3,3,3,3; 4,4,4,4,4]; rabxquad = [0, 1; 0, 6; 5,11; 5, 6]; rabyquad = [18,23; 23,28; 23,28; 18,23]; rabzquad = [1,1; 1,1; 1,1; 1,1]; rabquadcolor_byface = [2 2]; rabquadcolor = [2,2; 3,3; 4,4; 5,5]; subplot(2,2,2); plot3d(rabxtri, rabytri, list(rabztri,rabtricolor)); plot3d(rabxquad,rabyquad,list(rabzquad,rabquadcolor)); h = gcf(); h.children(1).background = 1; xtitle('A psychedelic rabbit set of patches'); subplot(2,2,4); plot3d(rabxtri, rabytri, list(rabztri,rabtricolor_byface)); plot3d(rabxquad,rabyquad,list(rabzquad,rabquadcolor_byface)); h = gcf(); h.children(1).background = 1; xtitle('A standard rabbit set of patches');
The result of the preceding example:
We can also use the plot3d function to plot a set of patches using vertex and faces.
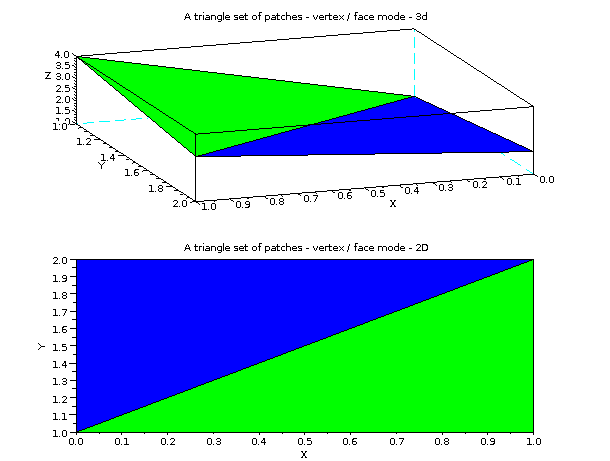
// Vertex / Faces example: 3D example // The vertex list contains the list of unique points composing each patch // The points common to 2 patches are not repeated in the vertex list vertex = [0 1 1; 0 2 2; 1 2 3; 1 1 4]; // The face list indicates which points are composing the patch. face = [1 2 3; 1 3 4]; tcolor = [2 3]'; // The formula used to translate the vertex / face representation into x, y, z lists xvf = matrix(vertex(face,1),size(face,1),length(vertex(face,1))/size(face,1))'; yvf = matrix(vertex(face,2),size(face,1),length(vertex(face,1))/size(face,1))'; zvf = matrix(vertex(face,3),size(face,1),length(vertex(face,1))/size(face,1))'; scf(); subplot(2,1,1); plot3d(xvf,yvf,list(zvf,tcolor)); xtitle('A triangle set of patches - vertex / face mode - 3d'); // 2D test // We use the 3D representation with a 0 Z values and then switch to 2D representation // Vertex / Faces example: 3D example // The vertex list contains the list of unique points composing each patch // The points common to 2 patches are not repeated in the vertex list vertex = [0 1; 0 2; 1 2; 1 1]; // The face list indicates which points are composing the patch. face = [1 2 3; 1 3 4]; // The formula used to translate the vertex / face representation into x, y, z lists xvf = matrix(vertex(face,1),size(face,1),length(vertex(face,1))/size(face,1))'; yvf = matrix(vertex(face,2),size(face,1),length(vertex(face,1))/size(face,1))'; zvf = matrix(zeros(vertex(face,2)),size(face,1),length(vertex(face,1))/size(face,1))'; subplot(2,1,2); plot3d(xvf,yvf,list(zvf,tcolor)); xtitle('A triangle set of patches - vertex / face mode - 2D'); a = gca(); a.view = '2d';
The result of the preceding example:
How to set manually some ticks
plot3d(); h = gca(); h.x_ticks = tlist(['ticks','locations','labels'],[-2,-1,0,1,2],['-2','-1','0','1','2']); h.y_ticks = tlist(['ticks','locations','labels'],[-4,-3-2,-1,0,1,2,3,4],['-4','-3','-2','-1','0','1','2','3','4']); h.z_ticks = tlist(['ticks','locations','labels'],[-1,0,1],['Point 1','Point 2','Point 3']);
Ver Também
- eval3dp — computa facetas 3d de uma superfície parametrizada
- genfac3d — computa facetas de uma superfície 3d
- geom3d — projeção 3d para 2d após um esboço 3d
- param3d — esboço 3d de uma curva parametrizada
- plot3d1 — Esboço 3d em níveis de cinza ou de cores de uma superfície
- clf — Limpa ou reajusta a (janela da) figura gráfica corrente para valores padrões
- gca — Retorna o manipulador da entidade Axes corrente
- gcf — Retorna o manipulador da janela GUI ou de gráficos corrente.
- xdel — deleta uma janela de gráficos
- delete — Deleta uma entidade gráfica e seus galhos
- axes_properties — descrição das propriedades de entidades Axes (de eixos)
Autor
J.Ph.C.
| << param3d_properties | 3d_plot | plot3d1 >> |