Recherche de racines

Description

Certains problèmes requièrent la détection de passage de zéro de fonctions continues (par exemple, les systèmes de régulation). Tous les solveurs assurent cette foncionnalité, et est réalisée en suivant le même procédé.

Chaque Zero-crossing Block définit une de ces fonctions, notées g(t).

En général, cette fonctionnalité ne trouve que les racines à multiplicité impaire, correspondant à un changement de signe de g(t). Si une de ces fonctions a une racine à multiplicité impaire (pas de changement de signe), elle ne sera probablement pas détectée. Si une telle racine est désirée, l'utilisateur doit reformuler la fonction pour qu'elle change de signe à l'endroit de la racine.

Le schéma utilisé est de vérifier les traversées de zéro de g(t) sur chaque pas de temps, puis (changement de signe détecté) de zoomer sur cette traversée (ou racine) grâce à une méthode des sécantes modifiée.

Après des vérifications et ajustements corrects, les racines sont recherchées dans [t_lo, t_hi] . On entre dans une boucle pour localiser la racine suivant une tolérance acceptable, donnée par l'arrondi de la machine, le temps actuel et le pas de temps.

On détermine alors quelle fonction racine a le plus de chances de voir sa racine arriver en première en comparant les valeurs de la méthode des sécantes, et on donne une nouvelle valeur t_mid et on restreint l'intervalle de recherche à [t_lo, t_mid] ou [t_mid, t_hi] , suivant dans lequel le changement de signe se produit.

Puisque la tolérance dépend du pas de temps, plus ce dernier est faible, plus la précision sera grande.

Exemples et Analyse du temps de calcul

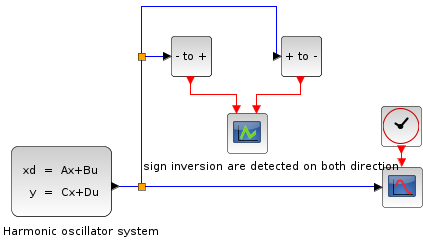
Exemple simple d'une fonction Sinus traversant zéro plusieurs fois :

// Import du diagramme et réglage du temps final
loadScicos();
loadXcosLibs();
importXcosDiagram("SCI/modules/xcos/demos/Threshold_ZeroCrossing.zcos");

// Lancement du chronomètre, de la simulation et affichage du temps
tic();
try xcos_simulate(scs_m, 4); catch disp(lasterror()); end
t = toc();
disp("Temps pour LSodar :", t);

Les barres bleues représentent les traversées "positif vers négatif", et les rouges "négatif vers positif".

Dans les scripts suivants, on test le surplus de calcul de la détection de racines avec LSodar :

D'abord, un Sinus traversant zéro toutes les π périodes : Ouverture du script

Temps avec recherche de racine :
 15.021

Temps sans recherche de racine :
 10.573
            

Ensuite, une simple ligne droite traversant zéro une seule fois, au milieu de l'intervalle : Ouverture du script

Temps avec recherche de racine :
 0.114

Temps sans recherche de racine :
 0.09
            

Suivant le nombre de racines, l'aspect de la fonction à l'approche de ces racines, les tolérances, ..., le surplus de temps de calcul va de 25% à 45%.

Voir Aussi

• LSodar — LSodar (abréviation de "Livermore Solver for Ordinary Differential equations, with Automatic method switching for stiff and nonstiff problems, and with Root-finding") est un solveur numérique fournissant une méthode efficace et stable pour résoudre des Problèmes à Valeur Initiale d'Equations Différentielles Ordinaires (EDOs).
• CVode — CVode (abréviation de "C-language Variable-coefficients ODE solver") est un solveur numérique fournissant une méthode efficace et stable pour résoudre des Problèmes à Valeur Initiale d'Equations Différentielles Ordinarires (EDOs). Il utilise BDF ou Adams comme méthode d'intégration, et des itérations fonctionnelles ou de Newton.
• IDA — "Implicit Differential Algebraic equations system solver" est un solveur numérique fournissant une méthode efficace et stable pour résoudre des Problèmes à Valeur Initiale d'Equations Différentielles Algebriques (EDAs).
• Runge-Kutta 4(5) — Runge-Kutta est un solveur numérique fournissant une méthode explicite efficace pour résoudre des Problèmes à Valeur Initiale d'Equations Différentielles Ordinarires (EDOs).
• Dormand-Prince 4(5) — Dormand-Prince est un solveur numérique fournissant une méthode explicite efficace pour résoudre des Problèmes à Valeur Initiale d'Equations Différentielles Ordinarires (EDOs).
• Runge-Kutta Implicite 4(5) — Solveur numérique fournissant une méthode implicite efficace et stable pour résoudre des Problèmes à Valeur Initiale d'Equations Différentielles Ordinarires (EDOs)
• Crank-Nicolson 2(3) — Crank-Nicolson est un solveur numérique basé sur le schéma Runge-Kutta fournissant une méthode implicite efficace et stable pour résoudre des Problèmes à Valeur Initiale d'Equations Différentielles Ordinaires (EDOs). Appelé par xcos.
• DDaskr — "Double-precision Differential Algebraic equations system Solver with Krylov method and Rootfinding" : solveur numérique fournissant une méthode efficace et stable pour résoudre des Problèmes à Valeur Initiale d'Equations Différentielles Algebriques (EDAs).
• Comparaisons — Cette page compare les solveurs pour déterminer lequel est le mieux adapté au le problème étudié.
• ode — solveur d'équations différentielles ordinaires
• ode_discrete — ordinary differential equation solver, discrete time simulation
• ode_root — ordinary differential equation solver with roots finding
• odedc — discrete/continuous ode solver
• dae — Solveur de système d'Equations Différentielles Algébriques

Bibliographie

Documentation Sundials