DDaskr

"Double-precision Differential Algebraic equations system Solver with Krylov method and Rootfinding" : solveur numérique fournissant une méthode efficace et stable pour résoudre des Problèmes à Valeur Initiale d'Equations Différentielles Algebriques (EDAs).

Description

Appelé par xcos, DDaskr (abréviation de "Double-precision Differential Algebraic equations system Solver with Krylov method and Rootfinding") est un solveur numérique fournissant une méthode efficace et stable pour résoudre des Problèmes à Valeur Initiale de la forme :

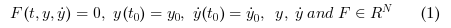
$\begin{eqnarray} F(t,y,\dot{y}) = 0, \hspace{2 mm} y(t_0)=y_0, \hspace{2 mm} \dot{y}(t_0)=\dot{y}_0, \hspace{3 mm} y, \hspace{1.5 mm} \dot{y} \hspace{1.5 mm} and \hspace{1.5 mm} F \in R^N \hspace{10 mm} (1) \end{eqnarray}$

Avant de résoudre le problème, DDaskr lance une routine interne pour trouver des valeurs consistantes à y₀ et yPrime₀ .

Partant alors de ces y₀ et yPrime₀ , DDaskr approxime y_n+1 grâce à la formule BDF :

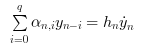
$\begin{eqnarray} \sum_{i=0}^{q} \alpha_{n,i} y_{n-i} = h_n\dot{y}_{n} \end{eqnarray}$

avec, comme dans CVode, y_n l'approximation de y(t_n) , h_n = t_n - t_n-1 la taille du pas, et les coefficients fixés, déterminés uniformément par le type de méthode, son ordre q allant de 1 à 5 et l'histoire des pas de temps.

Injecter cette formule dans (1) fournit le système :

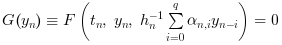
$G(y_n) \equiv F \left( t_n, \hspace{1.5mm} y_n, \hspace{1.5mm} h_n^{-1}\sum_{i=0}^{q} \alpha_{n,i} y_{n-i} \right) = 0$

Sa résolution s'effectue par la méthode de Newton, mais les itérations sont soit directes soit de Krylov (GMRes préconditionnées).

Itération Directe : on commence par réécrire le système :

$J \left[y_{n(m+1)}-y_{n(m)} \right] = -G(y_{n(m)})$

avec J une approximation du Jacobien :

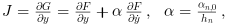
$J = \frac{\partial{G}}{\partial{y}} = \frac{\partial{F}}{\partial{y}}+\alpha\frac{\partial{F}}{\partial{\dot{y}}}, \hspace{4 mm} \alpha = \frac{\alpha_{n,0}}{h_n},$

α change quand le pas ou l'ordre de la méthode varient.

Un solveur direct dense est alors utilisé et on poursuit sur le prochain pas de temps.
Méthode de GMRes Krylov : d'abord, on préconditionne le système en appliquant le Jacobien mentionné au-dessus.

Ensuite, on déterminela base le l'espace de Krylov suivant et on recalcule la matrice de Hessenberg.

Premier test de convergence. S'il ne passe pas, on calcule le résidu, qui conduit à une potentielle nouvelle solution, et on itère jusuq'à ce que le résidu converge.

DDaskr se sert des valeurs passées pour contrôler l'erreur locale y_n(m) - y_n(0) et recalcule h_n si cette erreur n'est pas satisfaisante.

Cette fonction est appelée entre les activations, parce-que'une acrtivation discrète peut modifier le système.

Suivant la criticalité de l'événement (son effet sur le problème continu), soit le solveur poursuit avec temps initial et final différents comme si rien ne s'était passé, soit, si le système a été modifié, il faut "réinitialiser à froid" le solveur et le relancer.

En moyenne, DDaskr accepte des tolérances juqu'à 10^-11. Au-delà, il retourne l'erreur Trop de précision demandée.

Pour l'instant, DDaskr ne peut être appliqué qu'à des systèmes où les fonctions dont on cherche à détecter les traversées de zéro sont poncutellement nulles, et non nulles sur un segment.

Exemple

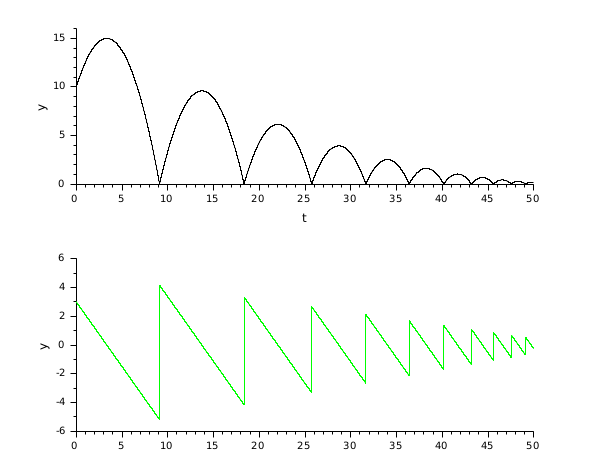
Le bloc 'Modelica Generic' retourne ses états continus, on peut les évaluer avec DDaskr en lançant l'exemple:

Voir Aussi

LSodar — LSodar (abréviation de "Livermore Solver for Ordinary Differential equations, with Automatic method switching for stiff and nonstiff problems, and with Root-finding") est un solveur numérique fournissant une méthode efficace et stable pour résoudre des Problèmes à Valeur Initiale d'Equations Différentielles Ordinaires (EDOs).
CVode — CVode (abréviation de "C-language Variable-coefficients ODE solver") est un solveur numérique fournissant une méthode efficace et stable pour résoudre des Problèmes à Valeur Initiale d'Equations Différentielles Ordinarires (EDOs). Il utilise BDF ou Adams comme méthode d'intégration, et des itérations fonctionnelles ou de Newton.
IDA — "Implicit Differential Algebraic equations system solver" est un solveur numérique fournissant une méthode efficace et stable pour résoudre des Problèmes à Valeur Initiale d'Equations Différentielles Algebriques (EDAs).
Runge-Kutta 4(5) — Runge-Kutta est un solveur numérique fournissant une méthode explicite efficace pour résoudre des Problèmes à Valeur Initiale d'Equations Différentielles Ordinarires (EDOs).
Dormand-Prince 4(5) — Dormand-Prince est un solveur numérique fournissant une méthode explicite efficace pour résoudre des Problèmes à Valeur Initiale d'Equations Différentielles Ordinarires (EDOs).
Runge-Kutta Implicite 4(5) — Solveur numérique fournissant une méthode implicite efficace et stable pour résoudre des Problèmes à Valeur Initiale d'Equations Différentielles Ordinarires (EDOs)
Crank-Nicolson 2(3) — Crank-Nicolson est un solveur numérique basé sur le schéma Runge-Kutta fournissant une méthode implicite efficace et stable pour résoudre des Problèmes à Valeur Initiale d'Equations Différentielles Ordinaires (EDOs). Appelé par xcos.
Comparaisons — Cette page compare les solveurs pour déterminer lequel est le mieux adapté au le problème étudié.
dae — Solveur de système d'Equations Différentielles Algébriques
ode — solveur d'équations différentielles ordinaires
ode_discrete — ordinary differential equation solver, discrete time simulation
ode_root — ordinary differential equation solver with roots finding
odedc — discrete/continuous ode solver

Bibliographie

Netlib, documentation à l'intérieur du code.

Documentation Sundials

Histoire

Version	Description
5.5.0	DDaskr ajouté

Report an issue
<< IDA	Solveurs	Recherche de racines >>

Copyright (c) 2022-2024 (Dassault Systèmes)
Copyright (c) 2017-2022 (ESI Group)
Copyright (c) 2011-2017 (Scilab Enterprises)
Copyright (c) 1989-2012 (INRIA)
Copyright (c) 1989-2007 (ENPC)
with contributors

Last updated:
Thu Oct 24 11:16:04 CEST 2024