ndgrid
строит матрицы или N-мерные массивы путем репликации данных векторов
Синтаксис
[X, Y] = ndgrid(x) [X, Y] = ndgrid(x,y) [X, Y, Z] = ndgrid(x,y,z) [X, Y, Z, T] = ndgrid(x,y,z,t) [X1, X2, ..., Xm] = ndgrid(x1,x2,...,xm)
Аргументы
- x, y, z, ...
векторы любых типов данных. Они могут иметь различные типы данных. По умолчанию
y=x.- X, Y, Z, ...
В случае двух входных аргументов это матрицы, в противном случае это гиперматрицы. Все они имеют одинаковые размеры:
size(x,"*")строк,size(y,"*")столбцов,size(z,"*")слоёв и так далее.Они имеют одинаковые типы данных соответствющих входных векторов:
typeof(X)==typeof(x),typeof(Y)==typeof(y), и т.д.
Описание
Первое применение функции ndgrid заключается в построении сетки
узлов, формирующих двумерное, трёхмерное или N-мерное пространство в соответствии с
2, 3 и более наборами x, y и т.д. координат
"шаблона" продискретизированных вдоль каждого направления/размерности пространства,
которое вы желаете сформировать.
Следовательно, матрица или гиперматрица X сделана через копирование
вектора x по столбцам; матрица или гиперматрица Y
сделана через копирование вектора y по строкам; матрица Z
сделана через копирование вектора z по всем слоям (третье измерение);
и т.д
--> [X, Y] = ndgrid([1 3 4], [0 2 4 6]) X = 1. 1. 1. 1. 3. 3. 3. 3. 4. 4. 4. 4. Y = 0. 2. 4. 6. 0. 2. 4. 6. 0. 2. 4. 6.
Эта схема копирования может быть обобщена к любому числу измерений, а также к любому типу универсальных данных. Давайте, например, возьмём 2 атрибута:
- Первый - это число, которое нужно выбрать из вектора, скажем
n = [ 3 7 ] - Второй - это буква, которую нужно выбрать из вектора, скажем
c = ["a" "e" "i" "o" "u" "y"]
{n,c} возможных пар.
Это будет просто двумерная сетка:
--> [N, C] = ndgrid([3 7],["a" "e" "i" "o" "u" "y"]) C = !a e i o u y ! !a e i o u y ! N = 3. 3. 3. 3. 3. 3. 7. 7. 7. 7. 7. 7.
Тогда object(i,j) будет иметь свойства {n(i) c(j)},
которые темер могут быть адресованы как {N(i,j) C(i,j)}.
Такой вид сетки может быть полезен для инициализации массива структур.
Следующие примеры показывают как использовать X, Y, Z в
наиболее распространёных приложениях
Примеры
Пример #1:
// создание простой двухмерной координатной сетки x = linspace(-10,2,40); y = linspace(-5,5,40); [X,Y] = ndgrid(x,y); // Compute ordinates Z(X,Y) on the {X, Y} grid and plot Z(X,Y) Z = X - 3*X.*sin(X).*cos(Y-4) ; clf() plot3d(x,y,Z, flag=[color("green") 2 4], alpha=7, theta=60); show_window()
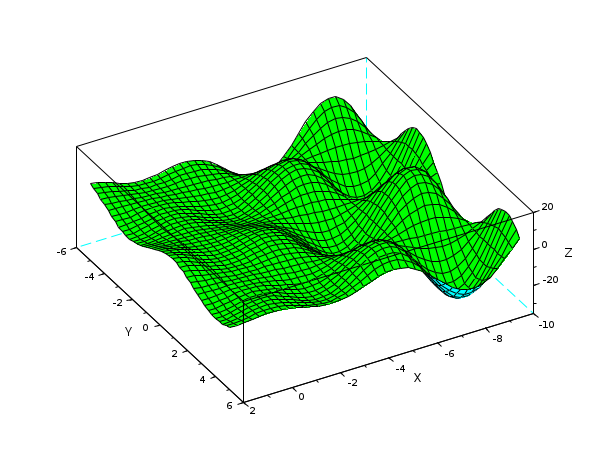
Пример #2:
// создание простой трёхмерной координатной сетки nx = 10; ny = 6; nz = 4; x = linspace(0,2,nx); y = linspace(0,1,ny); z = linspace(0,0.5,nz); [X,Y,Z] = ndgrid(x,y,z); // попытаемся отобразить эту трёхмерную координатную сетку ... XF=[]; YF=[]; ZF=[]; for k=1:nz [xf,yf,zf] = nf3d(X(:,:,k), Y(:,:,k), Z(:,:,k)); XF = [XF xf]; YF = [YF yf]; ZF = [ZF zf]; end for j=1:ny [xf,yf,zf] = nf3d(matrix(X(:,j,:),[nx,nz]),.. matrix(Y(:,j,:),[nx,nz]),.. matrix(Z(:,j,:),[nx,nz])); XF = [XF xf]; YF = [YF yf]; ZF = [ZF zf]; end clf() plot3d(XF,YF,ZF, flag=[0 6 3], 66, 61, leg="X@Y@Z") xtitle("Трёхмерная сетка!"); show_window()

Пример #3: Создание таблицы пар символов:
[c1, c2] = ndgrid(["a" "b" "c"], ["a" "b" "c" "d" "e" "f" "g" "h"]) c1+c2
--> [c1, c2] = ndgrid(["a" "b" "c"], ["a" "b" "c" "d" "e" "f" "g" "h"]) c2 = !a b c d e f g h ! !a b c d e f g h ! !a b c d e f g h ! c1 = !a a a a a a a a ! !b b b b b b b b ! !c c c c c c c c ! --> c1+c2 ans = !aa ab ac ad ae af ag ah ! !ba bb bc bd be bf bg bh ! !ca cb cc cd ce cf cg ch !
Смотрите также
История
| Версия | Описание |
| 6.0.0 | Расширение до всех однородных типов данных ([], логические, закодированные целые числа, многочлены, дроби, строковые значения). Пересмотр этой странички справки. |
| 6.0.1 | ndgrid(x) теперь принимает по умолчанию y=x. |
| Report an issue | ||
| << meshgrid | Элементарные матрицы | ones >> |