fft
прямое или обратное Быстрое Преобразование Фурье вектора, матрицы или гиперматрицы
ifft
обратное быстрое преобразование Фурье
Синтаксис
X = fft(A) X = fft(A, sign) X = fft(A, sign, directions) X = fft(A, sign, dims, incr) X = fft(.., symmetry)
Аргументы
- A, X
- векторы, матрицы или многомерные массивы вещественных или комплексных чисел одинаковых размеров.
- sign
- -1 или 1 : знак множителя
±2iπв экспоненциальном члене формулы преобразования, устанавливающий прямое или обратное преобразование. По умолчанию значение равно-1, соответствующее прямому преобразованию. - directions
- вектор, содержащий индексы размерности
A(в[1, ndims(A)]) вдоль которой необходимо вычислить БПФ (многомерный). По умолчанию направленияdirectionsсоответствуют1:ndims(A): "кумулятивный" БПФ вычисляется для всех направлений. См. раздел "Описание". - symmetry
- необязательная символьная строка, помогающая функции
fft()выбрать наилучший алгоритм:- "symmetric": заставляет
рассматривать
Aили все её "слои" как симметрично сопряжённую. Это полезно, когда точная симметрияAили её "слоёв" возможно чередуется только из-за ошибок округления. Многомерный массивBразмерами[s1,s2,..,sN]сопряжённо симметричный для БПФ, если и только еслиB==conj(B([1 s1:-1:2],[1 s2:-1:2],...,[1 sN:-1:2])). В этом случае результатXявляется вещественным и может использоваться эффективный специфический алгоритм для его вычисления. - "nonsymmetric": Тогда
fft()не обращает внимание ни на какую симметрию. - не указано: тогда выполняется автоматическое определение симметрии.
- "symmetric": заставляет
рассматривать
- dims
- вектор положительных целых чисел. Старый синтаксис.
Каждый элемент должен быть делителем
length(A). Произведение элементов должно быть строго меньшеlength(A). См. подробности в разделе "Описание". - incr
- вектор положительных строго возрастающих целых чисел, такой же
длины, что и
dims. Старый синтаксис. Каждый элемент должен быть делителемlength(A). См. подробности в разделе "Описание".
Описание
Эта функция вычисляет прямое или обратное одно-, дву- или многомерное дискретное преобразование Фурье массива или многомерного массива чисел вдоль одного или нескольких направлений внутри этого массива.
Краткий синтаксис
Прямое преобразование:
X = fft(A [,symmetry]) или
X = fft(A, -1 [,symmetry]) выполняет прямое
преобразование.
- одномерное
a=Aявляется вектором: вычисляется одномерное прямое БПФ, так что: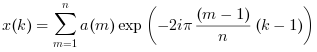
- многомерное
Aявляется матрицей или многомерным массивом: выполняется многомерное прямое БПФ.
Обратное нормированное преобразование:
X = fft(A,+1) или X = ifft(A)
выполняет обратное нормированное преобразование, такое, что
A==ifft(fft(A)).
- одномерное
a=Aявляется вектором:X = fft(a, +1)илиX = ifft(a)выполняют одномерное обратное БПФ, вычисляемое как: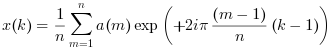
- многомерное
Aявляется матрицей или многомерным массивом: выполняется многомерное обратное БПФ.
Длинный синтаксис: многомерное прямое БПФ
X = fft(A, sign, directions [, symmetry])
выполняет эффективно все прямые или обратные БПФ по всем "слоям"
A вдоль выбранных направлений directions.
Например, если A является трёхмерным массивом, то
X = fft(A,-1,2) эквивалентно:
и X = fft(A,-1,[1 3]) эквивалентно:
for i2 = 1:size(A,2) X(:,i2,:) = fft(A(:,i2,:), -1); end
X = fft(A, sign, dims, incr [, symmetry])
является старым синтаксисом, который также позволяет выполнять все
прямые или обратные БПФ слоёв A вдоль выбранных
направлений directions. С этим синтаксисом
A рассматривается как сериализованная в вектор, и
её фактические размеры игнорируются. Слои выбираются указанием
размеров A и инкрементов сериализованного индекса,
относящегося к размерам.
Например, если A является массивом с
n1*n2*n3 элементов,
X = fft(A,-1, n1, 1) эквивалентно
X = fft(matrix(A,[n1,n2,n3]), -1, 1) ;
а X = fft(A,-1, [n1 n3], [1 n1*n2])
эквивалентно
X = fft(matrix(A,[n1,n2,n3]), -1, [1,3]).
Оптимизация fft
Примечание:
Функция fft() автоматически сохраняет свои последние
внутренние параметры в памяти для повторного их использования во
второй раз. Это значительно улучшает время вычисления, когда
выполняются последовательные вызовы (с одинаковыми параметрами).
Можно пойти дальше в оптимизации fft(), используя
функции
get_fftw_wisdom и
set_fftw_wisdom.
Алгоритмы:
fft() использует библиотеку
fftw3.
Библиография: Matteo Frigo and Steven G. Johnson, "FFTW Documentation" http://www.fftw.org/#documentation
Примеры
Одномерное БПФ (вектора):
// Частотные составляющие сигнала //------------------------------- // построение зашумлённого сигнала оцифрованного с частотой 1000 Гц, содержащего чистые // гармоники на 50 и 70 Гц sample_rate = 1000; t = 0:1/sample_rate:0.6; N = size(t,'*'); //количество отсчётов s = sin(2*%pi*50*t) + sin(2*%pi*70*t+%pi/4) + grand(1,N,'nor',0,1); y=fft(s); // s является вещественным и результат БПФ является сопряжённо симметричным и мы // оставляем только первые N/2 точек f = sample_rate*(0:(N/2))/N; //вектор связанных частот n = size(f,'*') clf() plot(f, abs(y(1:n)))
2D FFT (of a matrix):
A = zeros(256,256); A(5:24,13:17) = 1; X = fftshift(fft(A)); set(gcf(), "color_map",jet(128)); clf; grayplot(0:255, 0:255, abs(X)')
N-мерный БПФ (многомерного массива):
// простой случай, 3 одномерных БПФ во времени N = 2048; t = linspace(0,10,2048); A = [2*sin(2*%pi*3*t) + sin(2*%pi*3.5*t) 10*sin(2*%pi*8*t) sin(2*%pi*0.5*t) + 4*sin(2*%pi*0.8*t)]; X = fft(A,-1,2); fs = 1/(t(2)-t(1)); f = fs*(0:(N/2))/N; // вектор связанных частот clf; plot(f(1:100)',abs(X(:,1:100))') legend(["3 и 3,5 Гц","8 Гц","0,5 и 0,8 Гц"],"in_upper_left") // 45 трёхмерных БПФ во времени Dims = [5 4 9 5 6]; A = matrix(rand(1, prod(Dims)), Dims); y = fft(A,-1,[2 4 5]); // эквивалентный (но менее эффективный) код y1 = zeros(A); for i1 = 1:Dims(1) for i3 = 1:Dims(3) ind = list(i1,:,i3,:,:); y1(ind(:)) = fft(A(ind(:)),-1); end end
// Использование явной формулы одномерного дискретного преобразования Фурье // ------------------------------------------------------------------------ function xf=DFT(x, Sign); n = size(x,'*'); // вычисление матрицы Фурье размером n на n am = exp(Sign * 2*%pi*%i * (0:n-1)'*(0:n-1)/n); xf = am * matrix(x,n,1); // ДПФ xf = matrix(xf,size(x)); // изменение размерности if Sign == 1 then xf = xf/n; end endfunction // Сравнение с алгоритмом БПФ a = rand(1,1000); norm(DFT(a,1) - fft(a,1)) norm(DFT(a,-1) - fft(a,-1)) tic(); DFT(a,-1); toc() tic(); fft(a,-1); toc()
Смотрите также
- corr — корреляция, ковариация
- fftw_flags — устанавливают метод вычисления быстрого преобразования Фурье функции fftw
- get_fftw_wisdom — возврат опыта fftw
- set_fftw_wisdom — Устанавливает опыт fftw
- fftw_forget_wisdom — Сброс опыта fftw
| Report an issue | ||
| << dst | transforms | fft2 >> |