Scilab Website | Contribute with GitLab | Mailing list archives | ATOMS toolboxes
Scilab Online Help
2023.1.0 - Português


CLSS

Continuous state-space system

Block Screenshot

Contents

Description

This block realizes a continuous-time linear state-space system.

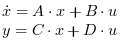
\begin{matrix} \dot{x} = A \cdot x + B \cdot u \\ y = C \cdot x + D \cdot u \end{matrix}

where x is the vector of state variables, u is the vector of input functions and y is the vector of output variables.

The system is defined by the (A, B, C, D) matrices and the initial state X0. The dimensions must be compatible.

Parameters

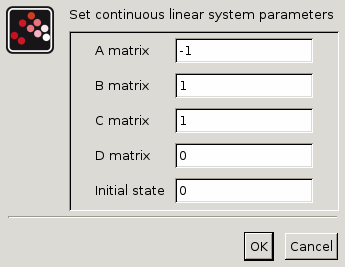
  • A matrix

    A square matrix.

    Properties : Type 'mat' of size [-1,-1].

  • B matrix

    The B matrix, [] if system has no input.

    Properties : Type 'mat' of size ["size(%1,2)","-1"].

  • C matrix

    The C matrix , [] if system has no output.

    Properties : Type 'mat' of size ["-1","size(%1,2)"].

  • D matrix

    The D matrix, [] if system has no D term.

    Properties : Type 'mat' of size [-1,-1].

  • Initial state

    A vector/scalar initial state of the system.

    Properties : Type 'vec' of size "size(%1,2)".

Default properties

  • always active: yes

  • direct-feedthrough: no

  • zero-crossing: no

  • mode: no

  • regular inputs:

    - port 1 : size [1,1] / type 1

  • regular outputs:

    - port 1 : size [1,1] / type 1

  • number/sizes of activation inputs: 0

  • number/sizes of activation outputs: 0

  • continuous-time state: yes

  • discrete-time state: no

  • object discrete-time state: no

  • name of computational function: csslti4

Interfacing function

  • SCI/modules/scicos_blocks/macros/Linear/CLSS.sci

Computational function

  • SCI/modules/scicos_blocks/src/c/csslti4.c (Type 4)

Example

This sample example illustrates how to use CLSS block to simulate and display the output waveform y(t)=Vc(t) of the RLC circuit shown below.

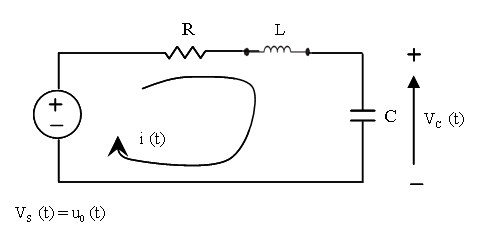
The equations for an RLC circuit are the following. They result from Kirchhoff's voltage law and Newton's law.

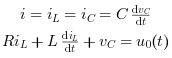
\begin{matrix} i = i_L = i_C = C \frac{\mathrm{d} v_C }{\mathrm{d} t} \\ Ri_L + L \frac{\mathrm{d} i_L }{\mathrm{d} t} + v_C = u_0(t) \end{matrix}

The R, L and C are the system's resistance, inductance and capacitor.

We define the capacitor voltage Vc and the inductance current iL as the state variables X1 and X2.

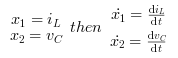
\begin{array}{c} \mbox{$x_1 = i_L$}\\ \mbox{$x_2 = v_C$}\\ \end{array} then \begin{array}{c} \mbox{$\dot{x_1} = \frac{\mathrm{d} i_L }{\mathrm{d} t}$}\\ \mbox{$\dot{x_2} = \frac{\mathrm{d} v_C }{\mathrm{d} t}$} \end{array}

thus

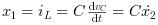
x_1 = i_L = C\frac{\mathrm{d} v_C }{\mathrm{d} t} = C\dot{x_2}

Rearranging these equations we get:

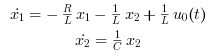
\begin{array}{c} \dot{x_1} = -\frac{R}{L} x_1 - \frac{1}{L} x_2 + \frac{1}{L} u_0(t) \\ \dot{x_2} = \frac{1}{C} x_2 \end{array}

These equations can be put into matrix form as follows,

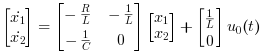
\begin{bmatrix}\dot{x_1}\\\dot{x_2}\end{bmatrix} = \begin{bmatrix} -\frac{R}{L} & -\frac{1}{L}\\ -\frac{1}{C} & 0 \end{bmatrix} \begin{bmatrix}x_1\\x_2\end{bmatrix} + \begin{bmatrix}\frac{1}{L}\\0\end{bmatrix} u_0(t)

The required output equation is

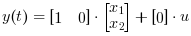
y(t) = \begin{bmatrix} 1 & 0 \end{bmatrix} \cdot \begin{bmatrix} x_{1} \\ x_{2} \end{bmatrix} + \begin{bmatrix} 0 \end{bmatrix} \cdot u

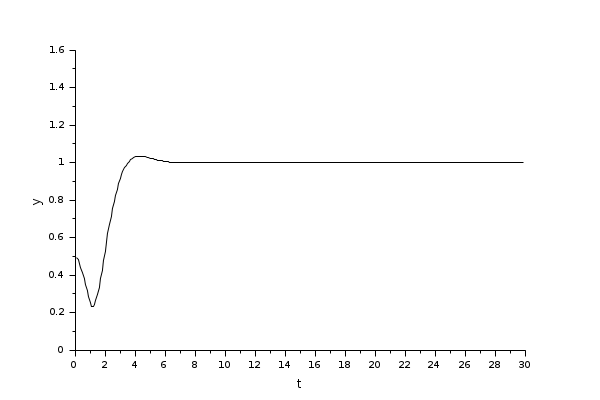
The following diagram shows these equations modeled in Xcos where R= 10 Ω, L= 5 mΗ and C= 0.1 µF; the initial states are x1=0 and x2=0.5.

To obtain the output Vc(t) we use CLSS block from Continuous time systems Palette.

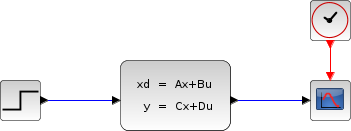
Report an issue
<< CLR Continuous_pal DERIV >>
Copyright (c) 2022-2024 (Dassault Systèmes)
Copyright (c) 2017-2022 (ESI Group)
Copyright (c) 2011-2017 (Scilab Enterprises)
Copyright (c) 1989-2012 (INRIA)
Copyright (c) 1989-2007 (ENPC)
with contributors 		Last updated:
Mon May 22 12:42:15 CEST 2023