ordmmd
複数の最小次元順序付けを計算する
呼び出し手順
[perm,invp,nofsub]=ordmmd(xadj,iadj,n)
引数
- n
double、整数値の1行1列の行列,方程式の数
- xadj
double、整数値の(n+1)行1列の行列,Aの行へのポインタ
- iadj
double、整数値のnnz行1列の行列,Aの行添字
- perm
double、整数値のn行1列の行列,最小次元規則配列
- invp
double、整数値のn行1列の行列,permの逆行列
- nofsub
double、整数値の1行1列の行列,圧縮記憶方式における非ゼロ要素の数の上限
説明
コレスキー分解を適用する前に対称疎行列の行および列を交換する際に 最小次元アルゴリズムが使用されます. このアルゴリズムはコレスキー分解の非ゼロ要素の数を減らします.
n行n列の実対称疎行列Aを指定すると,
このコレスキー分解 U は,通常,
Aの上三角要素よりも非ゼロ要素が多くなる
"塗りつぶし(fill in)"に苦しめられます.
行列P'*A*Pが同じく対称で,
そのコレスキー分解の非ゼロ要素の数が最小となる
交換行列 Pを探します.
例
以下の例では,対称疎行列の順序付けを計算します.
隣接構造体を計算する際にsp2adj を使用します.
A = [ 4. 1. 2. 0.5 2. 1. 0.5 0. 0. 0. 2. 0. 3. 0. 0. 0.5 0. 0. 5./8. 0. 2. 0. 0. 0. 16. ]; A = sparse(A); [xadj,iadj,val]=sp2adj(A); n = size(A,"r"); [perm,invp,nofsub]=ordmmd(xadj,iadj,n)
以下の例では,対称疎行列の順序付けを計算します.
invpがpermの
逆行列であることを確認します.
A = [ 0., 0., 0., 2., 0., 0., 2., 0., 2., 0., 0. ; 0., 0., 4., 0., 0., 0., 0., 0., 0., 0., 0. ; 0., 4., 0., 0., 0., 0., 0., 0., 0., 0., 0. ; 2., 0., 0., 0., 0., 0., 2., 0., 2., 0., 0. ; 0., 0., 0., 0. , 0., 0., 0., 0., 0., 0., 4. ; 0., 0., 0., 0., 0., 0., 0., 3., 0., 3., 0. ; 2., 0., 0., 2., 0., 0., 0., 0., 2., 0., 0. ; 0., 0., 0., 0., 0., 3., 0., 0., 0., 3., 0. ; 2., 0., 0., 2., 0., 0., 2., 0., 0., 0., 0. ; 0., 0., 0., 0., 0., 3., 0., 3., 0., 0., 0. ; 0., 0., 0., 0., 4., 0., 0., 0., 0., 0., 0.]; n=size(A,1); A=sparse(A); [xadj,adjncy,anz]=sp2adj(A); [perm,invp,nofsub]=ordmmd(xadj,adjncy,n); perm(invp)
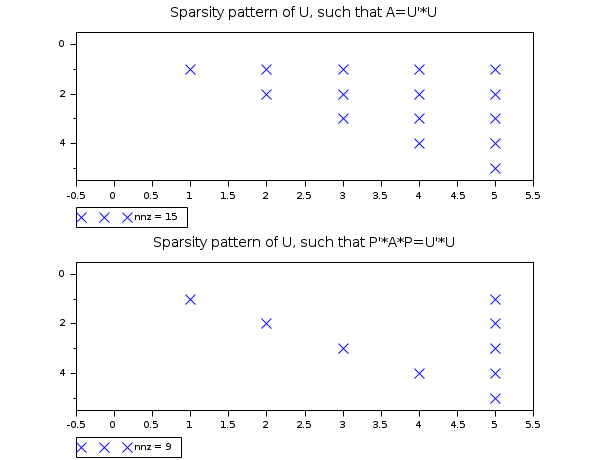
以下の例では, 行列Aと行列P'*A*P
のコレスキー分解の疎パターンを計算します.
"Computer Solution of Large Sparse Positive Definite Systems"のp.3 "Chapter 1: Introduction"を参照.
コレスキー分解の非ゼロ要素の数は15,一方,行列P'*A*Pのコレスキー分解は
9個の非ゼロ要素を有することがわかります.
A = [ 4. 1. 2. 0.5 2. 1. 0.5 0. 0. 0. 2. 0. 3. 0. 0. 0.5 0. 0. 5./8. 0. 2. 0. 0. 0. 16. ]; A = sparse(A); // Aのコレスキー分解の疎パターンを調べる U = sparse(chol(full(A))); scf(); subplot(2,1,1); PlotSparse(U,"x"); xtitle("Sparsity pattern of U, such that A=U''*U"); // 隣接構造体を取得 [xadj,iadj,val]=sp2adj(A); // 複数の最小次元規則配列を計算 n = size(A,"r"); [perm,invp,nofsub]=ordmmd(xadj,iadj,n); // 交換ベクトルを行列に変換 P=spzeros(n,n); for i=1:n P(perm(i),i)=1; end // P'*A*Pのコレスキー分解の疎パターンを調べる U = sparse(chol(full(P'*A*P))); subplot(2,1,2); PlotSparse(U,"x"); xtitle("Sparsity pattern of U, such that P''*A*P=U''*U");
実装に関する注記
この関数はMathematical Sciences Section, Oak Ridge National Laboratoryの Esmond G. Ng および Barry W. Peytonによる ソースコード "ordmmd.f",に基づいています. アルゴリズムはSPARSPAKライブラリのJoseph W.H. Liuによる genmmdルーチンに基づいています.
参考文献
"Minimum degree algorithm", Wikipedia contributors, Wikipedia, The Free Encyclopedia. http://en.wikipedia.org/wiki/Minimum_degree_algorithm
"A new release of SPARSPAK: the Waterloo sparse matrix package", Alan George and Esmond Ng. 1984. SIGNUM Newsl. 19, 4 (October 1984), 9-13.
"Computer Solution of Large Sparse Positive Definite Systems" by Alan George and Joseph Liu, Prentice-Hall, Inc. Englewood Cliffs, New Jersey, 1981
"Implementation of Lipsol in Scilab", Rubio Scola, 1997, INRIA, No 0215
| Report an issue | ||
| << chsolve | Sparses Matrix | UMFPACK Interface >> |