flts
time response (discrete time, sampled system)
Syntax
y = flts(u, sl) y = flts(u, sl, past) y = flts(u, sl, x0) [y,x] = flts(u, sl, x0)
Arguments
- u
matrix (input vector)
- sl
A linear dynamical system, in state space, transfer function or zpk representations, in discrete time.
- x0
vector (initial state ; default value=
0)- past
matrix (of the past ; default value=
0)- x,y
matrices (state and output)
Description
State-space form:
sl is a discrete linear system given by its state
space representation (see syslin ):
sl=syslin('d',A,B,C,D) :
x[t+1] = A x[t] + B u[t] y[t] = C x[t] + D u[t]
or, more generally, if D is a polynomial matrix
(p = degree(D(z))) :
D(z) = D_0 + z D_1 + z^2 D_2 +..+ z^p D_p y[t] = C x[t] + D_0 u[t] + D_1 u[t+1] +..+ D_[p] u[t+p]
Transfer form:
y=flts(u,sl[,past]). Here sl
is a linear system in transfer matrix representation i.e
sl=syslin('d',transfer_matrix) (see
syslin
).
past = [u ,..., u ]
[ -nd -1]
[y ,..., y ]
[ -nd -1]
is the matrix of past values of u and y.
nd is the maximum of degrees of lcm's of each row
of the denominator matrix of sl.
u = [u0 u1 ... un] (input) y = [y0 y1 ... yn] (output)
p is the difference between maximum degree of numerator and maximum degree of denominator
Examples
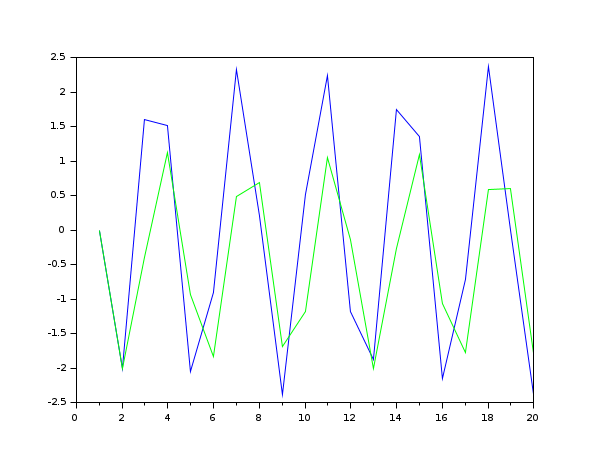
sl=syslin('d',1,1,1);u=1:10; y=flts(u,sl); plot2d(y) [y1,x1]=flts(u(1:5),sl);y2=flts(u(6:10),sl,x1); y-[y1,y2] //With polynomial D: z=poly(0,'z'); D=1+z+z^2; p =degree(D); sl=syslin('d',1,1,1,D); y=flts(u,sl);[y1,x1]=flts(u(1:5),sl); y2=flts(u(5-p+1:10),sl,x1); // (update) y-[y1,y2] //Delay (transfer form): flts(u,1/z) // Usual responses z=poly(0,'z'); h=syslin(0.1,(1-2*z)/(z^2+0.3*z+1)) imprep=flts(eye(1,20),tf2ss(h)); //Impulse response clf(); plot(imprep,'b') u=ones(1,20); stprep=flts(ones(1,20),tf2ss(h)); //Step response plot(stprep,'g')
// Other examples A=[1 2 3;0 2 4;0 0 1]; B=[1 0;0 0;0 1]; C=eye(3,3); Sys=syslin('d',A,B,C); H=ss2tf(Sys); u=[1;-1]*(1:10); // yh=flts(u,H); ys=flts(u,Sys); norm(yh-ys,1) //hot restart [ys1,x]=flts(u(:,1:4),Sys);ys2=flts(u(:,5:10),Sys,x); norm([ys1,ys2]-ys,1) // yh1=flts(u(:,1:4),H);yh2=flts(u(:,5:10),H,[u(:,2:4);yh(:,2:4)]); norm([yh1,yh2]-yh,1) //with D<>0 D=[-3 8;4 -0.5;2.2 0.9]; Sys=syslin('d',A,B,C,D); H=ss2tf(Sys); u=[1;-1]*(1:10); rh=flts(u,H); rs=flts(u,Sys); norm(rh-rs,1) //hot restart [ys1,x]=flts(u(:,1:4),Sys);ys2=flts(u(:,5:10),Sys,x); norm([ys1,ys2]-rs,1) //With H: yh1=flts(u(:,1:4),H);yh2=flts(u(:,5:10),H,[u(:,2:4); yh1(:,2:4)]); norm([yh1,yh2]-rh)
See also
History
| Version | Description |
| 6.0 | handling zpk representation |
| Report an issue | ||
| << dsimul | Domaine Temporel | ltitr >> |