grand

Arguments

m, n, o

integers, size of the wanted matrix / hypermatrix Y.

X

a matrix or hypermatrix whom only the dimensions (say m-by-n) are used.

Y

depending on the input, a matrix or hypermatrix, with random entries.

S

output of the action (a string or a real column vector).

Description

This function generates random numbers from various distributions.

The syntaxes:

Y = grand(m, n, "bet", A, B)
Y = grand(m, n, "bin", N, p)
Y = grand(m, n, "nbn", N, p)
Y = grand(m, n, "chi", Df)
Y = grand(m, n, "nch", Df, Xnon)
Y = grand(m, n, "exp", Av)
Y = grand(m, n, "f", Dfn, Dfd)
Y = grand(m, n, "nf", Dfn, Dfd, Xnon)
Y = grand(m, n, "gam", shape, rate)
Y = grand(m, n, "nor", Av, Sd)
Y = grand(m, n, "geom", p)
Y = grand(m, n, "poi", mu)
Y = grand(m, n, "def")
Y = grand(m, n, "unf", Low, High)
Y = grand(m, n, "uin", Low, High)
Y = grand(m, n, "lgi")

produce a m-by-n matrix with random entries. All these syntaxes can be extended to create a random hypermatrix with more than 2 dimensions specified as integers listed before the type of statistical distribution:

Y = grand(m, n, o, ..., "..", ...)

The sizes of the expected random vector, matrix or hypermatrix can alternatively be specified with

Y = grand(X, ...)

where X of sizes m-by-n... is a matrix or an hypermatrix only used as template.

The syntaxes:

Y = grand(n, "mn", Mean, Cov)
Y = grand(n, "markov", P, x0)
Y = grand(n, "mul", nb, P)
Y = grand(n, "prm", vect)

produce a m-by-n matrix with random entries, where m is the size of the argument Mean, Cov, P or vect depending on the case (see below for details).

The syntaxes:

S = grand("getgen")
grand("setgen", gen)

S = grand("getsd")
grand("setsd", S)

grand("setcgn", G)
S = grand("getcgn")

grand("initgn", I)

grand("setall", s1, s2, s3, s4)

grand("advnst", K)

configure or query the state of the underlying random number generators.

Getting random numbers from a given distribution

beta

Y = grand(m, n, "bet", A, B) generates random variates from the beta distribution with parameters A and B. The density of the beta distribution is (0 < x < 1):

A and B must be reals >10^-37. Related function: cdfbet.

binomial

Y = grand(m, n, "bin", N, p) generates random variates from the binomial distribution with parameters N (positive integer) and p (real in [0,1]): number of successes in N independent Bernouilli trials with probability p of success. Related functions: binomial, cdfbin.

negative binomial

Y = grand(m, n, "nbn", N, p) generates random variates from the negative binomial distribution with parameters N (positive integer) and p (real in (0,1)) : number of failures occurring before N successes in independent Bernoulli trials with probability p of success. Related function: cdfnbn.

chi-square

Y = grand(m, n, "chi", Df) generates random variates from the chi-square distribution with Df (real > 0.0) degrees of freedom. Related function: cdfchi.

non-central chi-square

Y = grand(m, n, "nch", Df, Xnonc) generates random variates from the non-central chisquare distribution with Df degrees of freedom (real >= 1.0) and noncentrality parameter Xnonc (real >= 0.0). Related function: cdfchn.

exponential

Y = grand(m, n, "exp", Av) generates random variates from the exponential distribution with mean Av (real > 0.0).

F variance ratio

Y = grand(m, n, "f", Dfn, Dfd) generates random variates from the F (variance ratio) distribution with Dfn (real > 0.0) degrees of freedom in the numerator and Dfd (real > 0.0) degrees of freedom in the denominator. Related function : cdff.

non-central F variance ratio

Y = grand(m, n, "nf", Dfn, Dfd, Xnonc) generates random variates from the noncentral F (variance ratio) distribution with Dfn (real >= 1) degrees of freedom in the numerator, and Dfd (real > 0) degrees of freedom in the denominator, and noncentrality parameter Xnonc (real >= 0). Related function : cdffnc.

gamma

Y = grand(m, n, "gam", shape, rate) generates random variates from the gamma distribution with parameters shape (real > 0) and rate (real > 0). The density of the gamma distribution is :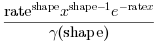

Related functions : gamma, cdfgam.

Gauss Laplace (normal)

Y = grand(m, n, "nor", Av, Sd) generates random variates from the normal distribution with mean Av (real) and standard deviation Sd (real >= 0). Related function : cdfnor.

multivariate gaussian (multivariate normal)

Y = grand(n, "mn", Mean, Cov) generates multivariate normal random variates; Mean must be a m x 1 column vector and Cov a m-by-m symmetric positive definite matrix (Y is then a m-by-n matrix).

geometric

Y = grand(m, n, "geom", p) generates random variates from the geometric distribution with parameter p : number of Bernouilli trials (with probability success of p) until a success is met. p must be in [1.3e-307, 1]).

Y contains positive real numbers with integer values, whiсh are the "number of trials to get a success".

markov

Y = grand(n, "markov", P, x0) generate n successive states of a Markov chain described by the transition matrix P. A sum of each the rows in P is 1. Initial state is given by x0. If x0 is a matrix of size m=size(x0,"*") then Y is a matrix of size m-by-n. Y(i,:) code the sample path obtained from initial state x0(i).

multinomial

Y = grand(n, "mul", nb, P) generates n observations from the Multinomial distribution : class nb events in m categories (put nb "balls" in m "boxes"). P(i) is the probability that an event will be classified into category i. The column vector of probabilities P is of size m-1 (the probability of category m is 1-sum(P)). Y is of size m-by-n. Each column Y(:,j) is an observation from multinomial distribution and Y(i,j) is the number of events falling in category i (for the j-th observation) (sum(Y(:,j)) = nb).

Poisson

Y = grand(m, n, "poi", mu) generates random variates from the Poisson distribution with mean mu (real >= 0.0). Related function: cdfpoi.

random permutations

Y = grand(n, "prm", vect) generates n random permutations of vect. vect can be a column vector of reals, or a vector, matrix or hypermatrix of complexes, integers, booleans, polynomials or strings; full or sparse. Due to the stack structure, vect should not and cannot be a row vector. This feature covers Matlab's randperm() function, because randperm(n) is equivalent to grand(1,'prm',(1:n)') and randperm(n, k) can be obtained through grand(1,'prm',(1:n)'); ans(1:k).

uniform (def)

Y = grand(m, n, "def") generates random variates from the uniform distribution over [0,1) (1 is never returned).

uniform (unf)

Y = grand(m, n, "unf", Low, High) generates random reals uniformly distributed in [Low, High) (High is never returned).

uniform (uin)

Y = grand(m, n, "uin", Low, High) generates random integers uniformly distributed between Low and High (included). High and Low must be integers such that (High-Low+1) < 2,147,483,561.

uniform (lgi)

Y = grand(m, n, "lgi") returns the basic output of the current generator : random integers following a uniform distribution over :

• [0, 2^32 - 1] for mt and kiss;

• [0, 2^31 - 87] for clcg2;

• [0, 2^31 - 2] for clcg4;

• [0, 2^31 - 1] for urand.

Set/get the current generator and its state

The user has the possibility to choose between different base generators (which give random integers following the "lgi" distribution, the others being gotten from it).

mt

The Mersenne-Twister of M. Matsumoto and T. Nishimura, period about 2^19937, state given by an array of 624 integers (plus an index onto this array); this is the default generator.

kiss

The "Keep It Simple Stupid" of G. Marsaglia, period about 2^123, state given by four integers.

clcg2

A Combined 2 Linear Congruential Generator of P. L'Ecuyer, period about 2^61, state given by 2 integers.

clcg4

A Combined 4 Linear Congruential Generator of P. L'Ecuyer, period about 2^121, state given by 4 integers ; this one is split in 101 different virtual (non-overlapping) generators which may be useful for different tasks (see "Options specific to clcg4" and "Test example for clcg4").

urand

The generator used by the scilab function rand, state given by 1 integer, period of 2^31. This generator is based on "Urand, A Universal Random Number Generator" By, Michael A. Malcolm, Cleve B. Moler, Stan-Cs-73-334, January 1973, Computer Science Department, School Of Humanities And Sciences, Stanford University. This is the faster of this list but its statistical qualities are less satisfactory than the other generators.

The different actions common to all the generators, are:

action = "getgen"

S = grand("getgen") returns the current base generator. In this case S is a string among "mt", "kiss", "clcg2", "clcg4", "urand".

action = "setgen"

grand("setgen",gen) sets the current base generator to be gen a string among "mt", "kiss", "clcg2", "clcg4", "urand". Notice that this call returns the new current generator, i.e. gen.

action = "getsd"

S = grand("getsd") gets the current state (the current seeds) of the current base generator ; S is given as a column vector (of integers) of dimension 625 for mt (the first being an index in [1,624]), 4 for kiss, 2 for clcg2, 4 for clcg4 (for this last one you get the current state of the current virtual generator) and 1 for urand.

action = "setsd"

grand("setsd", S) and grand("setsd", s1[, s2, s3, s4]) set the state of the current base generator (the new seeds) :

for mt

S is a vector of integers of dim 625 (the first component is an index and must be in [1,624], the 624 last ones must be in [0,2^32[) (but must not be all zeros) ; a simpler initialization may be done with only one integer s1 (s1 must be in [0,2^32[) ;

for kiss

four integers s1, s2, s3, s4 in [0,2^32[ must be provided ;

for clcg2

two integers s1 in [1,2^31-86] and s2 in [1,2^31-250] must be given ;

for clcg4

four integers s1 in [1,2^31-2], s2 in [1,2^31-106], s3 in [1,2^31-226], s4 in [1,2^31-326] are required ;

With clcg4 you set the seeds of the current virtual generator but you may lost the synchronization between this one and the others virtual generators (i.e. the sequence generated is not warranty to be non-overlapping with a sequence generated by another virtual generator) => use instead the "setall" option.

for urand

1 integer s1 in [0,2^31[ must be given.

action = "phr2sd"

Sd = grand("phr2sd", phrase) given a phrase (character string) generates a 1 x 2 vector Sd which may be used as seeds to change the state of a base generator (initially suited for clcg2).

Options specific to clcg4

The clcg4 generator may be used as the others generators but it offers the advantage to be split in several (101) virtual generators with non-overlapping sequences (when you use a classic generator you may change the initial state (seeds) in order to get another sequence but you are not warranty to get a complete different one). Each virtual generator corresponds to a sequence of 2^72 values which is further split into V=2^31 segments (or blocks) of length W=2^41. For a given virtual generator you have the possibility to return at the beginning of the sequence or at the beginning of the current segment or to go directly at the next segment. You may also change the initial state (seed) of the generator 0 with the "setall" option which then change also the initial state of the other virtual generators so as to get synchronization, i.e. in function of the new initial state of gen 0 the initial state of gen 1..100 are recomputed so as to get 101 non-overlapping sequences.

action = "setcgn"

grand("setcgn",G) sets the current virtual generator for clcg4 (when clcg4 is set, this is the virtual (clcg4) generator number G which is used); the virtual clcg4 generators are numbered from 0,1,...,100 (and so G must be an integer in [0,100]) ; by default the current virtual generator is 0.

action = "getcgn"

S = grand("getcgn") returns the number of the current virtual clcg4 generator.

action = "initgn"

grand("initgn", I) reinitializes the state of the current virtual generator

I = -1

sets the state to its initial seed

I = 0

sets the state to its last (previous) seed (i.e. to the beginning of the current segment)

I = 1

sets the state to a new seed W values from its last seed (i.e. to the beginning of the next segment) and resets the current segment parameters.

action = "setall"

grand("setall", s1, s2, s3, s4) sets the initial state of generator 0 to s1, s2, s3, s4. The initial seeds of the other generators are set accordingly to have synchronization. For constraints on s1, s2, s3, s4 see the "setsd" action.

action = "advnst"

grand("advnst", K) advances the state of the current generator by 2^K values and resets the initial seed to that value.

Examples

In the following example, we generate random numbers from various distributions and plot the associated histograms.

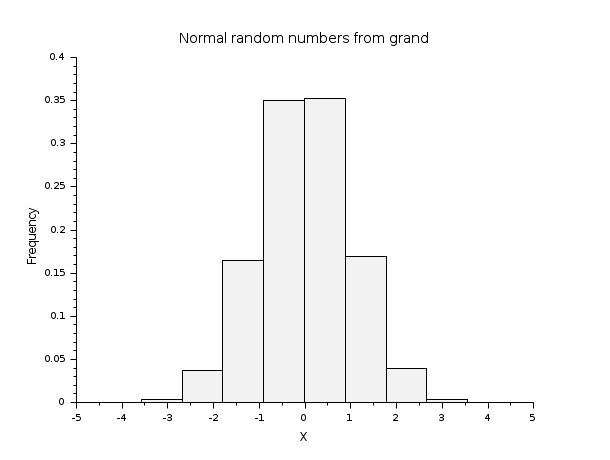
// Returns a 400-by-800 matrix of random doubles,
// with normal distribution and average 0 and standard deviation 1.
R = grand(400,800,"nor",0,1);
scf();
histplot(10,R);
xtitle("Normal random numbers from grand","X","Frequency");

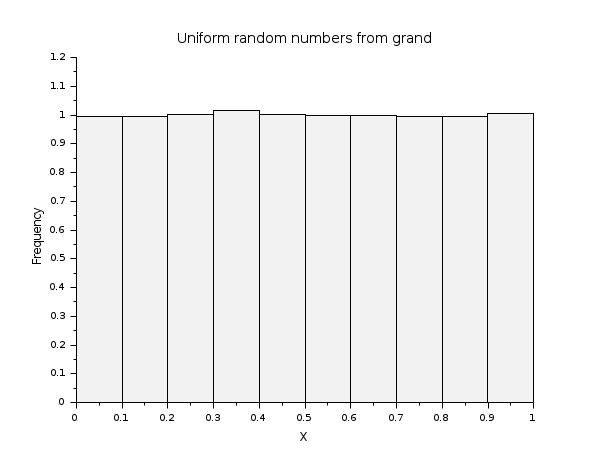
// Returns a 400-by-800 matrix of random doubles,
// uniform in [0,1).
R = grand(400,800,"def");
scf();
histplot(10,R);
xtitle("Uniform random numbers from grand","X","Frequency");

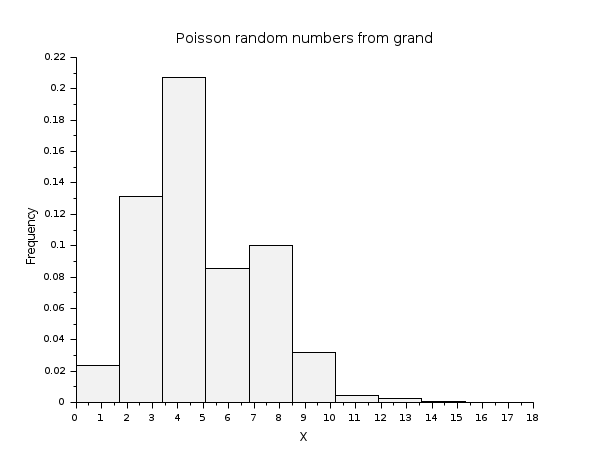
// Returns a 400-by-800 matrix of random doubles,
// with Poisson distribution and average equal to 5.
R = grand(400,800,"poi",5);
scf();
histplot(10,R);
xtitle("Poisson random numbers from grand","X","Frequency");

In the following example, we generate random numbers from the exponential distribution and then compare the empirical with the theoretical distribution.

lambda=1.6;
N=100000;
X = grand(1,N,"exp",lambda);
scf();
classes = linspace(0,12,25);
histplot(classes,X);
x=linspace(0,12,25);
y = (1/lambda)*exp(-(1/lambda)*x);
plot(x,y,"ro-");
legend(["Empirical" "Theory"]);
xtitle("Exponential random numbers from grand","X","Frequency");

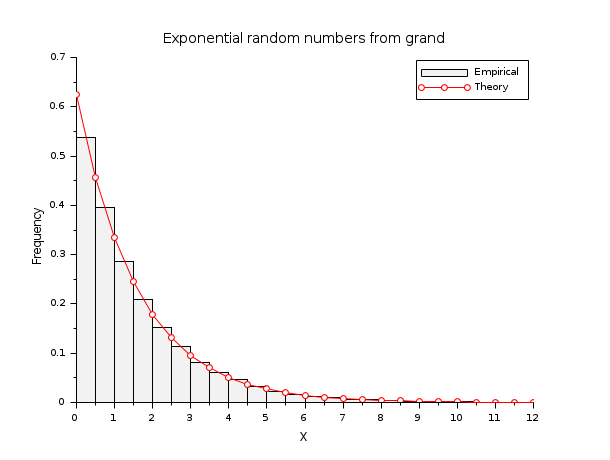
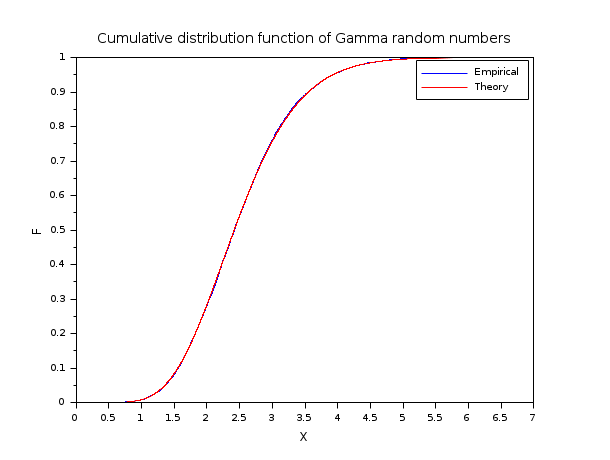
In the following example, we generate random numbers from the gamma distribution and then compare the empirical with the theoretical distribution.

N=10000;
A=10;
B=4;
R=grand(1,N,"gam",A,B);
XS=gsort(R,"g","i")';
PS=(1:N)'/N;
P=cdfgam("PQ",XS,A*ones(XS),B*ones(XS));
scf();
plot(XS,PS,"b-"); // Empirical distribution
plot(XS,P,"r-"); // Theoretical distribution
legend(["Empirical" "Theory"]);
xtitle("Cumulative distribution function of Gamma random numbers","X","F");

In the following example, we generate 10 random integers in the [1,365] interval.

grand(10,1,"uin",1,365)

In the following example, we generate 12 permutations of the [1,2,...,7] set. The 12 permutations are stored column-by-column.

grand(12,"prm",(1:7)')

In the following example, we generate a 10-by-10-by-10 hypermatrix of random numbers from the "normal" distribution and plot the associated histograms. Showing the first and last layers.

// Returns a 10-by-10-by-10 hypermatrix of random doubles,
// with normal distribution, average 0 and standard deviation 1.
// Showing the first and last layers.
R = grand(10,10,10,"nor",0,1);
subplot(1,2,1)
bar3d(R(:,:,1));
xtitle("Layer 1");
subplot(1,2,2)
bar3d(R(:,:,10));
xtitle("Layer 10");

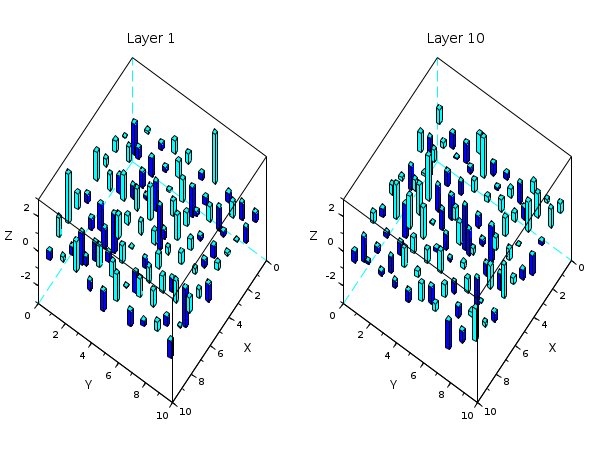
Get predictable or less predictable numbers

The pseudo random number generators are based on deterministic sequences. In order to get reproducible simulations, the initial seed of the generator is constant, such that the sequence will remain the same from a session to the other. Hence, by default, the first numbers produced by grand are always the same.

In some situations, we may want to initialize the seed of the generator in order to produce less predictable numbers. In this case, we may initialize the seed with the output of the getdate function:

n=getdate("s");
grand("setsd",n)

Test example for clcg4

An example of the need of the splitting capabilities of clcg4 is as follows. Two statistical techniques are being compared on data of different sizes. The first technique uses bootstrapping and is thought to be as accurate using less data than the second method which employs only brute force. For the first method, a data set of size uniformly distributed between 25 and 50 will be generated. Then the data set of the specified size will be generated and analyzed. The second method will choose a data set size between 100 and 200, generate the data and analyze it. This process will be repeated 1000 times. For variance reduction, we want the random numbers used in the two methods to be the same for each of the 1000 comparisons. But method two will use more random numbers than method one and without this package, synchronization might be difficult. With clcg4, it is a snap. Use generator 0 to obtain the sample size for method one and generator 1 to obtain the data. Then reset the state to the beginning of the current block and do the same for the second method. This assures that the initial data for method two is that used by method one. When both have concluded, advance the block for both generators.

See also

• rand — gerador de números randômico
• sprand — matriz esparsa randômica
• ssrand — gerador de sistema randômico
• randpencil — feixe aleatório
• genmarkov — gera uma matriz de Markov aleatória com classes recorrentes e transientes