arl2
L2伝達関数近似による SISO モデル実現
呼び出し手順
h=arl2(y,den0,n [,imp]) h=arl2(y,den0,n [,imp],'all') [den,num,err]=arl2(y,den0,n [,imp]) [den,num,err]=arl2(y,den0,n [,imp],'all')
引数
- y
z^-1の実数ベクトルまたは多項式で, 有理数システムの(インパルス応答の)フーリエ級数近似の係数を有します.- den0
解の初期推定値を指定する多項式で,
poly(1,'z','c')とすることができます.- n
整数, 伝達関数近似の次数 (分母denの次数)
- imp
整数で値は
(0,1,2)のどれか (冗長モード)- h
伝達関数
num/denまたは'all'フラグが指定された場合は伝達行列 (列ベクトル)'all'.- den
多項式または多項式ベクトル,解の分母
- num
多項式または多項式ベクトル, 解の分子
- err
実数の定数またはベクトル , 各解のL2誤差
説明
[den,num,err]=arl2(y,den0,n [,imp]) は,
伝達関数num/denが安定で,そのインパルス応答が
無数のゼロ点で完結すると仮定したベクトル y を
(最小L2ノルムで)近似する
多項式対num および denを探します.
y(z) = y(1)(1/z)+y(2)(1/z^2)+ ...+ y(ny)(1/z^ny)の場合,
num/den - y(z)のL2ノルムは,errとなります.
n は多項式 denの次数です.
伝達関数num/denは,有理システムのフーリエ級数のL2近似です.
impの設定により様々な中間結果が出力されるようになります.
[den,num,err]=arl2(y,den0,n [,imp],'all') は,
多項式のベクトルnum および denに
問題のローカル最適解の集合を返します.
解は誤差について昇順にソートされます.
この場合, den0はすでに
poly(1,'z','c')であると仮定されます.
例
v = ones(1,20); clf(); plot2d([], [v';zeros(80,1)], 2, '051',' ',[1,-0.5,100,1.5]) [d,n,e] = arl2(v, poly(1,'z','c'),1) plot2d([], ldiv(n,d,100), 2, '000') [d,n,e] = arl2(v,d,3) plot2d([], ldiv(n,d,100), 3, '000') [d,n,e] = arl2(v,d,8) plot2d([], ldiv(n,d,100), 5, '000') [d,n,e] = arl2(v,poly(1,'z','c'),4,'all') plot2d([], ldiv(n(1),d(1),100), 10, '000')
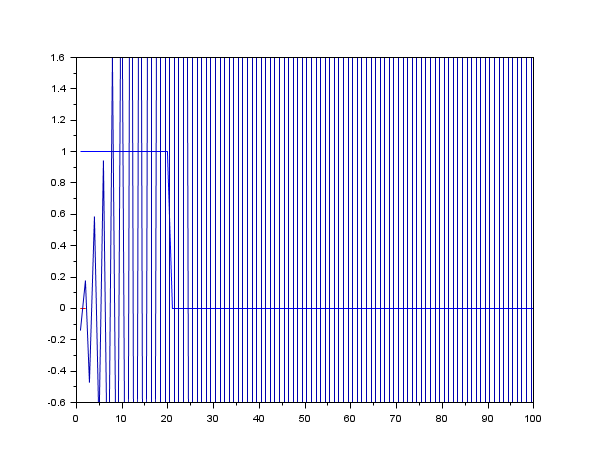
参照
| Report an issue | ||
| << Identification | Identification | armax >> |