bvode

Arguments

zu

a column vector of size M. The solution of the ode evaluated on the mesh given by points. It contains z(u(x)) for each requested points.

xpoints

an array which gives the points for which we want to observe the solution.

N

a scalar with integer value, number of differential equations (N <= 20).

m

a vector of size N with integer elements. It is the vector of order of each differential equation: m(i) gives the order of the i-th differential equation. In the following, M will represent the sum of the elements of m.

x_low

a scalar: left end of interval

x_up

a scalar: right end of interval

zeta

a vector of size M, zeta(j) gives j-th side condition point (boundary point). One must have x_low<=zeta(j) <=zeta(j+1)<=x_up

All side condition points must be mesh points in all meshes used, see description of ipar(11) and fixpnt below.

ipar

an array with 11 integer elements:

[nonlin, collpnt, subint, ntol, ndimf, ndimi, iprint, iread, iguess, rstart,nfxpnt]

nonlin: ipar(1)

0 if the problem is linear, 1 if the problem is nonlinear

collpnt: ipar(2)

Gives the number of collocation points per subinterval where max(m(j)) <= collpnt <= 7.

If ipar(2)=0 then collpnt is set to max( max(m(j))+1, 5-max(m(j)) ).

subint: ipar(3)

Gives the number of subintervals in the initial mesh. If ipar(3) = 0 then bvode arbitrarily sets subint = 5.

ntol: ipar(4)

Gives the number of solution and derivative tolerances. We require 0 < ntol <= M. ipar(4) must be set to the dimension of the tol argument or to 0. In the latter case the actual value will automatically be set to size(tol,'*').

ndimf: ipar(5)

Gives the dimension of fspace (a real work array). Its value provides a constraint on nmax the maximum number of subintervals.

The ipar(5) value must respect the constraint ipar(5)>=nmax*nsizef where nsizef=4 + 3*M + (5+collpnt*N)*(collpnt*N+M) + (2*M-nrec)*2*M (nrec is the number of right end boundary conditions).

ndimi: ipar(6)

Gives the dimension of ispace (an integer work array). Its value provides a constraint on nmax, the maximum number of subintervals.

The ipar(6) value must respect the constraint ipar(6)>=nmax*nsizei where nsizei= 3 + collpnt*N + M.

iprint: ipar(7)

output control, may take the following values:

-1: for full diagnostic printout
0: for selected printout
1: for no printout

iread: ipar(8)

= 0

causes bvode to generate a uniform initial mesh.

= xx

Other values are not implemented yet in Scilab

= 1: if the initial mesh is provided by the user it is defined in fspace as follows: the mesh will occupy fspace(1), ..., fspace(n+1). The user needs to supply only the interior mesh points fspace(j) = x(j),j = 2, ..., n.
= 2: if the initial mesh is supplied by the user as with ipar(8)=1, and in addition no adaptive mesh selection is to be done.

iguess: ipar(9)

= 0: if no initial guess for the solution is provided.
= 1: if an initial guess is provided by the user through the argument guess.
= 2: if an initial mesh and approximate solution coefficients are provided by the user in fspace (the former and new mesh are the same).
= 3: if a former mesh and approximate solution coefficients are provided by the user in fspace, and the new mesh is to be taken twice as coarse; i.e. every second point from the former mesh.
= 4: if in addition to a former initial mesh and approximate solution coefficients, a new mesh is provided in fspace as well (see description of output for further details on iguess = 2, 3 and 4).

ireg: ipar(10)

= 0: if the problem is regular
= 1: if the first relaxation factor is equal to ireg, and the nonlinear iteration does not rely on past convergence (use for an extra-sensitive nonlinear problem only)
= 2: if we are to return immediately upon (a) two successive nonconvergences, or (b) after obtaining an error estimate for the first time.

nfxpnt: ipar(11)

Gives the number of fixed points in the mesh other than x_low and x_up (the dimension of fixpnt). ipar(11) must be set to the dimension of the fixpnt argument or to 0. In the latter case the actual value will automatically be set to size(fixpnt,'*').

ltol

an array of dimension ntol=ipar(4). ltol(j) = l specifies that the j-th tolerance in the tol array controls the error in the l-th component of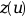 . It is also required that:

1 <= ltol(1) < ltol(2) < ... < ltol(ntol) <= M

tol

an array of dimension ntol=ipar(4).

tol(j) is the error tolerance on the ltol(j)-th component of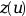 . Thus, the code attempts to satisfy 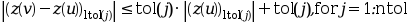on each subinterval

where is the approximate solution vector and 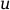is the exact solution (unknown).

fixpnt

an array of dimension nfxpnt=ipar(11). It contains the points, other than x_low and x_up, which are to be included in every mesh. The code requires that all side condition points other than x_low and x_up (see description of zeta) be included as fixed points in fixpnt.

fsub

an external used to evaluate the column vector f=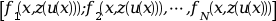 for any x such as x_low <= x <= x_up and for any z=z(u(x)) (see description below).

The external must have the headings:

In Fortran the calling sequence must be:

subroutine fsub(x,zu,f)
double precision zu(*), f(*),x

In C the function prototype must be:

void fsub(double *x, double *zu, double *f)

And in Scilab:
```
function f = fsub(x,zu,parameters)
```

dfsub

an external used to evaluate the Jacobian of f(x,z(u)) at a point x. Where z(u(x)) is defined as for fsub and the N by M array df should be filled by the partial derivatives of f: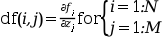

The external must have the headings:

In Fortran the calling sequence must be:

subroutine dfsub(x,zu,df)
double precision zu(*), df(*),x

In C the function prototype must be:

void dfsub(double *x, double *zu, double *df)

And in Scilab:
```
function df = dfsub(x,zu,parameters)
```

gsub

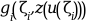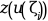
an external used to evaluate given z= z = zeta(i) for 1<=i<=M.

The external must have the headings:

In Fortran the calling sequence must be:

subroutine gsub(i,zu,g)
double precision zu(*), g(*)
integer i

In C the function prototype must be:

void gsub(int *i, double *zu, double *g)

And in Scilab:
```
function g = gsub(i,zu,parameters)
```
Note that in contrast to f in fsub, here only one value per call is returned in g.

dgsub

an external used to evaluate the i-th row of the Jacobian of g(x,u(x)). Where z(u) is as for fsub, i as for gsub and the M-vector dg should be filled with the partial derivatives of g, viz, for a particular call one calculates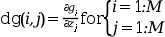

The external must have the headings:

In Fortran the calling sequence must be:

subroutine dgsub(i,zu,dg)
double precision zu(*), dg(*)

In C the function prototype must be

void dgsub(int *i, double *zu, double *dg)

And in Scilab
```
function dg = dgsub(i,zu,parameters)
```

guess

An external used to evaluate the initial approximation for z(u(x)) and dmval(u(x)) the vector of the mj-th derivatives of u(x). Note that this subroutine is used only if ipar(9) = 1, and then all M components of zu and N components of dmval should be computed for any x such as x_low <= x <= x_up.

The external must have the headings:

In Fortran the calling sequence must be:

subroutine guess(x,zu,dmval)
double precision x,z(*), dmval(*)

In C the function prototype must be

void fsub(double *x, double *zu, double *dmval)

And in Scilab

function [dmval,zu] = fsub(x,parameters)

<optional_args>

It should be either:

any left part of the ordered sequence of values: guess, dfsub, dgsub, fixpnt, ndimf, ndimi, ltol, tol, ntol,nonlin, collpnt, subint, iprint, ireg, ifail
or any sequence of arg_name=argvalue with arg_name in: guess, dfsub, dgsub, fixpnt, ndimf, ndimi, ltol, tol, ntol, nonlin, collpnt, subint, iprint, ireg, ifail

where all these arguments excepted ifail are described above. ifail can be used to display the bvode call corresponding to the selected optional arguments. If guess is given iguess is set to 1

Description

These functions solve a multi-point boundary value problem for a mixed order system of ode-s given by

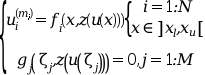
where

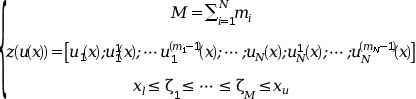
The argument zu used by the external functions and returned by bvode is the column vector formed by the components of z(u(x)) for a given x.

The method used to approximate the solution u is collocation at gaussian points, requiring m(i)-1 continuous derivatives in the i-th component, i = 1:N. here, k is the number of collocation points (stages) per subinterval and is chosen such that k ≥ max(m(i)). A runge-kutta-monomial solution representation is utilized.

Examples

The first two problems below are taken from the paper [1] of the Bibliography.

The problem 1 describes a uniformly loaded beam of variable stiffness, simply supported at both end.

It may be defined as follow :

Solve the fourth order differential equation:

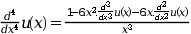
Subjected to the boundary conditions:

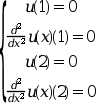
The exact solution of this problem is known to be:

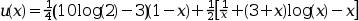
N = 1; // just one differential equation
m = 4; // a fourth order  differential equation
M = sum(m);

x_low = 1;
x_up = 2; // the x limits
zeta = [x_low,x_low,x_up,x_up]; // two constraints (on the value of u and its second derivative) on each bound.

// The external functions
// These functions are called by the solver with zu=[u(x);u'(x);u''(x);u'''(x)]

// - The function which computes the right hand side of the differential equation
function f=fsub(x, zu)
    f = (1-6*x^2*zu(4)-6*x*zu(3))/x^3
endfunction

// - The function which computes the derivative of fsub with respect to zu
function df=dfsub(x, zu)
    df = [0,0,-6/x^2,-6/x]
endfunction

// - The function which computes the ith constraint for a given i
function g=gsub(i, zu),
  select i
  case 1 then  // x = zeta(1) = 1
    g = zu(1)  // u(1) = 0
  case 2 then  // x = zeta(2) = 1
    g = zu(3)  // u''(1) = 0
  case 3 then  // x = zeta(3) = 2
    g = zu(1)  // u(2) = 0
  case 4 then  // x = zeta(4) = 2
    g = zu(3)  // u''(2) = 0
  end
endfunction

// - The function which computes the derivative of gsub with respect to z
function dg=dgsub(i, z)
  select i
  case 1 then  // x = zeta(1) = 1
    dg = [1,0,0,0]
  case 2 then  // x = zeta(2) = 1
    dg = [0,0,1,0]
  case 3 then  // x = zeta(3) = 2
    dg = [1,0,0,0]
  case 4 then  // x = zeta(4) = 2
    dg = [0,0,1,0]
  end
endfunction

// - The function which computes the initial guess, unused here
function [zu, mpar]=guess(x)
    zu = 0;
    mpar = 0;
endfunction

// define the function which computes the exact value of u for a given x ( for testing purposes)
function zu=trusol(x)
  zu = 0*ones(4,1)
  zu(1) =  0.25*(10*log(2)-3)*(1-x) + 0.5 *( 1/x   + (3+x)*log(x) - x)
  zu(2) = -0.25*(10*log(2)-3)       + 0.5 *(-1/x^2 + (3+x)/x      + log(x) - 1)
  zu(3) = 0.5*( 2/x^3 + 1/x   - 3/x^2)
  zu(4) = 0.5*(-6/x^4 - 1/x/x + 6/x^3)
endfunction

fixpnt = []; // All boundary conditions are located at x_low and x_up

//      nonlin  collpnt n ntol ndimf  ndimi iprint iread iguess rstart nfxpnt
ipar = [0       0       1 2    2000   200   1      0     0      0      0   ]

ltol = [1,3];          // set tolerance control on zu(1) and zu(3)
tol = [1.e-11,1.e-11]; // set tolerance values for these two controls
xpoints = x_low:0.01:x_up;

zu = bvode(xpoints,N,m,x_low,x_up,zeta,ipar,ltol,tol,fixpnt,...
           fsub,dfsub,gsub,dgsub,guess)
// check the constraints
zu([1,3],[1 $]) // should be zero
plot(xpoints,zu(1,:)) // the evolution of the solution u
zu1 = [];
for x = xpoints
    zu1 = [zu1,trusol(x)];
end
norm(zu-zu1)

Same problem using bvodeS and an initial guess.

function [z, lhS]=zstart(x)
    z = zeros(5,1); z(5) = 1;
    lhS = [0;1];
endfunction
zu = bvode(xpoints, N, m, x_low,x_up, zeta, ltol=ltol,tol=tol, guess=zstart)

The problem 2 describes the small finite deformation of a thin shallow spherical cap of constant thickness subject to a quadratically varying axisymmetric external pressure distribution. Here φ is the meridian angle change of the deformed shell and ψ is a stress function. For ε = μ = 10^-3, two different solutions may found depending on the starting point

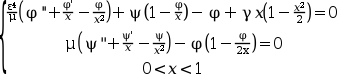
Subject to the boundary conditions

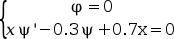
for x=0 and x=1

N = 2;     // two differential equations
m = [2 2]; // each differential equation is of second  order
M = sum(m);

x_low = 0;x_up=1; // the x limits
zeta = [x_low,x_low, x_up x_up]; // two  constraints on each bound.

// The external functions
// These functions are called by the solver with zu=[u1(x);u1'(x);u2(x);u2'(x)]

// - The function which computes the right hand side of the differential equation
function f=fsub2(x, zu, eps, dmu, eps4mu, gam, xt),
   f = [zu(1)/x^2-zu(2)/x+(zu(1)-zu(3)*(1-zu(1)/x)-gam*x*(1-x^2/2))/eps4mu //phi''
        zu(3)/x^2-zu(4)/x+zu(1)*(1-zu(1)/(2*x))/dmu];//psi''
endfunction

// - The function which computes the derivative of fsub with respect to zu
function df=dfsub2(x, zu, eps, dmu, eps4mu, gam, xt),
    df = [1/x^2+(1+zu(3)/x)/eps4mu, -1/x, -(1-zu(1)/x)/eps4mu, 0
         (1-zu(1)/x)/dmu             0    1/x^2              -1/x];
endfunction

// - The function which computes the ith constraint for a given i
function g=gsub2(i, zu),
  select i
  case 1 then  // x = zeta(1) = 0
    g = zu(1)  // u(0) = 0
  case 2 then  // x = zeta(2) = 0
    g = -0.3*zu(3) // x*psi'-0.3*psi+0.7x = 0
  case 3 then  // x = zeta(3) = 1
    g = zu(1)  // u(1) = 0
  case 4 then  // x = zeta(4) = 1
    g = 1*zu(4)-0.3*zu(3)+0.7*1 // x*psi'-0.3*psi+0.7x = 0
  end
endfunction

// - The function which computes the derivative of gsub with respect to z
function dg=dgsub2(i, z)
  select i
  case 1 then  // x = zeta(1) = 1
    dg = [1,0,0,0]
  case 2 then  // x = zeta(2) = 1
    dg = [0,0,-0.3,0]
  case 3 then  // x = zeta(3) = 2
    dg = [1,0,0,0]
  case 4 then  // x = zeta(4) = 2
    dg = [0,0,-0.3,1]
  end
endfunction

[gam, eps, dmu] = (1.1, 1d-3, 1d-3);
eps4mu = eps^4/dmu
xt = sqrt(2*(gam-1)/gam)

fixpnt = []; // All boundary conditions are located at x_low and x_up
collpnt = 4;
nsizef = 4 + 3*M + (5+collpnt*N)*(collpnt*N+M)+(2*M-2)*2*M ;
nsizei = 3 + collpnt*N+M;
nmax = 200;
//      nonlin  collpnt n  ntol  ndimf        ndimi       iprint iread iguess rstart nfxpnt
ipar = [1       collpnt 10  4   nmax*nsizef  nmax*nsizei   -1      0     0      0      0   ];

ltol = 1:4; // set tolerance control on zu(1), zu(2), zu(3) and zu(4)
tol = [1.e-5,1.e-5,1.e-5,1.e-5]; // set tolreance values for these four controls
xpoints = x_low:0.01:x_up;

// - The function which computes the initial guess, unused here
function [zu, dmval]=guess2(x, gam),
   cons = gam*x*(1-x^2/2)
   dcons = gam*(1-3*x^2/2)
   d2cons = -3*gam*x
   dmval = zeros(2,1)
   if x>xt then
     zu = [0 0 -cons -dcons]
     dmval(2) = -d2cons
   else
     zu = [2*x;2; -2*x+cons; -2*dcons]
     dmval(2) = d2cons
   end
endfunction

zu = bvode(xpoints,N,m,x_low,x_up,zeta,ipar,ltol,tol,fixpnt,...
           fsub2,dfsub2,gsub2,dgsub2,guess2);
scf(1); clf(); plot(xpoints,zu([1 3],:)) // the evolution of the solution phi and psi

// using an initial guess
ipar(9) = 1; // iguess

zu2 = bvode(xpoints,N,m,x_low,x_up,zeta,ipar,ltol,tol,fixpnt,...
            fsub2,dfsub2,gsub2,dgsub2,guess2);
scf(2); clf(); plot(xpoints,zu2([1 3],:)) // the evolution of the solution phi and psi

An eigenvalue problem:

// y''(x)=-la*y(x)
// BV: y(0)=y'(0); y(1)=0
// Eigenfunctions and eigenvalues are y(x,n)=sin(s(n)*(1-x)), la(n)=s(n)^2,
// where s(n) are the zeros of f(s,n)=s+atan(s)-(n+1)*pi, n=0,1,2,...
// To get a third boundary condition, we choose y(0)=1
// (With y(x) also c*y(x) is a solution for each constant c.)
// We solve the following ode system:
// y''=-la*y
// la'=0
// BV: y(0)=y'(0), y(0)=1; y(1)=0
// z=[y(x) ; y'(x) ; la]

function rhs=fsub(x, z)
  rhs = [-z(3)*z(1);0]
endfunction

function g=gsub(i, z)
  g = [z(1)-z(2) z(1)-1 z(1)]
  g = g(i)
endfunction

// The following start function is good for the first 8 eigenfunctions.
function [z, lhs]=ystart(x, z, la0)
  z = [1;0;la0]
  lhs = [0;0]
endfunction

[a, b, m, n] =(0, 1, [2;1], 2);
zeta = [a a b];
N = 101;
x = linspace(a,b,N)';

// We have s(n)-(n+1/2)*pi -> 0 for n to infinity.
la0 = evstr(x_dialog('n-th eigenvalue: n= ?','10'));
la0 = (%pi/2+la0*%pi)^2;

z = bvodeS(x,m,n,a,b,fsub,gsub,zeta,ystart=list(ystart,la0));
// The same call without any display
z = bvodeS(x,m,n,a,b,fsub,gsub,zeta,ystart=list(ystart,la0),iprint=1);
// The same with a lot of display
z = bvodeS(x,m,n,a,b,fsub,gsub,zeta,ystart=list(ystart,la0),iprint=-1);

clf()
plot(x,[z(1,:)' z(2,:)'])
xtitle(['Startvalue =  '+string(la0);'Eigenvalue = '+string(z(3,1))],'x',' ')
legend(['y(x)';'y''(x)']);

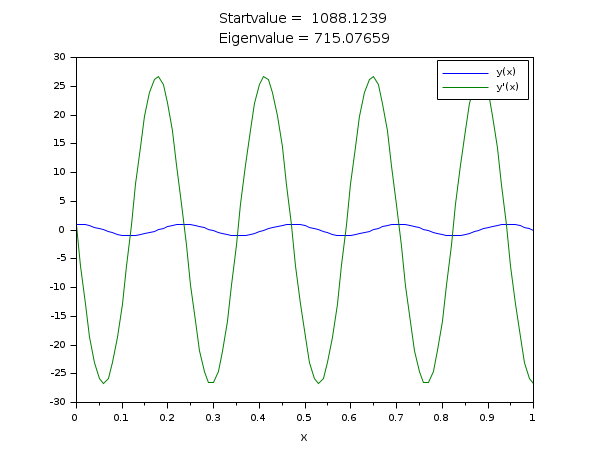
A boundary value problem with more than one solution.

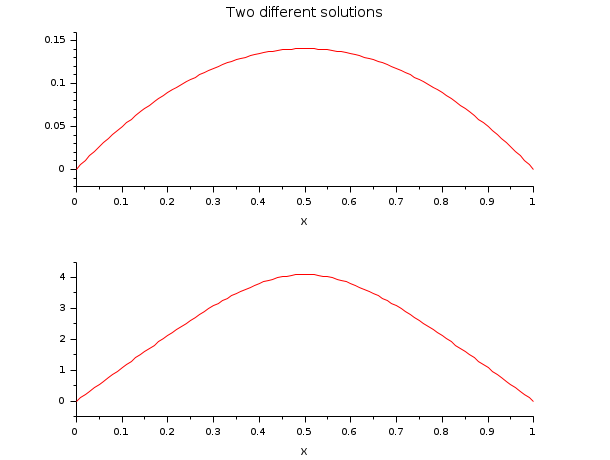
// DE: y''(x) = -exp(y(x))
// BV: y(0)=0; y(1)=0
// This boundary value problem has more than one solution.
// It is demonstrated how to find two of them with the help of
// some preinformation of the solutions y(x) to build the function ystart.
// z = [y(x);y'(x)]

[a, b, m, n] = (0, 1, 2, 1);
zeta = [a b];
N = 101;
tol = 1e-8*[1 1];
x = linspace(a,b,N);

function rhs=fsub(x, z)
  rhs = -exp(z(1))
endfunction

function g=gsub(i, z)
  g = [z(1) z(1)]
  g = g(i)
endfunction

function [z, lhs]=ystart(x, z, M)
  // z = [4*x*(1-x)*M ; 4*(1-2*x)*M]
  z = [M;0]
  //lhs = [-exp(4*x*(1-x)*M)]
  lhs = 0
endfunction

for M = [1 4]
   if M==1
      z = bvodeS(x,m,n,a,b,fsub,gsub,zeta,ystart=list(ystart,M),tol=tol);
   else
      z1 = bvodeS(x,m,n,a,b,fsub,gsub,zeta,ystart=list(ystart,M),tol=tol);
   end
end

// Integrating the ode yield e.g. the two solutions yex and yex1.

function y=f(c)
  y = c.*(1-tanh(sqrt(c)/4).^2)-2;
endfunction
c = fsolve(2,f);

function y=yex(x, c)
  y = log(c/2*(1-tanh(sqrt(c)*(1/4-x/2)).^2))
endfunction

function y=f1(c1), y=2*c1^2+tanh(1/4/c1)^2-1; endfunction
c1 = fsolve(0.1,f1);

function y=yex1(x, c1)
  y = log((1-tanh((2*x-1)/4/c1).^2)/2/c1/c1)
endfunction

disp('norm(yex(x)-z(1,:))= ', norm(z(1,:)-yex(x)))
disp('norm(yex1(x)-z1(1,:))= ', norm(z1(1,:)-yex1(x)))
clf();
subplot(2,1,1)
plot2d(x,z(1,:),style=[5])
xtitle('Two different solutions','x',' ')
subplot(2,1,2)
plot2d(x,z1(1,:),style=[5])
xtitle(' ','x',' ')

A multi-point boundary value problem.

// DE y'''(x)=1
// z = [y(x);y'(x);y''(x)]
// BV: y(-1)=2 y(1)=2
// Side condition: y(0)=1

a = -1; b = 1; c = 0;
// The side condition point c must be included in the array fixpnt.
n = 1;
m = 3;

function rhs=fsub(x, z)
  rhs = 1
endfunction

function g=gsub(i, z)
  g = [z(1)-2 z(1)-1 z(1)-2]
  g = g(i)
endfunction

N = 10;
zeta = [a c b];
x = linspace(a,b,N);

z = bvodeS(x,m,n,a,b,fsub,gsub,zeta,fixpnt=c);

function y=yex(x)
    y = x.^3/6 + x.^2 - x/6 + 1
endfunction

disp(norm(yex(x)-z(1,:)),'norm(yex(x)-z(1,:))= ')

Quantum Neumann equation, with 2 "eigenvalues" (c_1 and c2). Continuation being used.

// Quantum Neumann equation, with 2 "eigenvalues" c_1 and c_2
// (c_1=v-c_2-c_3, v is a parameter, used in continuation)
//
// diff(f,x,2) + (1/2)*(1/x + 1/(x-1) + 1/(x-y))*diff(f,x)
//      - (c_1/x + c_2/(x-1) + c_3/(x-y))* f(x) = 0
// diff(c_2,x)=0,  diff(c_3,x) = 0
//
// and 4 "boundary" conditions: diff(f,x)(a_k)=2*c_k*f(a_k) for
// k=1,2,3, a_k=(0, 1 , y)  and normalization f(1) = 1
//
// The z-vector is z_1=f, z_2=diff(f,x), z_3=c_2 and z_4=c_3
// The guess is chosen to have one node in [0,1],  f(x)=2*x-1
// such that f(1)=1, c_2 and c_3 are chosen to cancel poles in
// the differential equation at 1.0 and y, z_3=1, z_4=1/(2*y-1)
// Ref: http://arxiv.org/pdf/hep-th/0407005

y = 1.9d0;
eigens = zeros(3,40); // To store the results

// General setup for bvode

// Number of differential equations
ncomp = 3;

// Orders of equations
m = [2, 1, 1];

// Non-linear problem
ipar(1) = 1;

// Number of collocation points
ipar(2) = 3;

// Initial uniform mesh of 4 subintervals
ipar(3) = 4;
ipar(8) = 0;

// Size of fspace, ispace, see colnew.f to choose size
ipar(5) =  30000;
ipar(6) =  2000;

// Medium output
ipar(7) = 0;

// Initial approx is provided
ipar(9) = 1;

// fixpnt is an array containing all fixed points in the mesh, in
// particular "boundary" points, except aleft and aright, ipar[11] its
// size, here only one interior "boundary point"
ipar(11) = 1;
fixpnt = [1.0d0];

// Tolerances on all components z_1, z_2, z_3, z_4
ipar(4) = 4;

// Tolerance check on f and diff(f,x) and on c_2 and c_3
ltol = [1, 2, 3, 4];
tol = [1d-5, 1d-5, 1d-5, 1d-5];

// Define the differential equations

function [f]=fsub(x, z)
    f = [ -.5*(1/x+1/(x-1)+1/(x-y))*z(2) +...
     z(1) * ((v-z(3)-z(4))/x + z(3)/(x-1) + z(4)/(x-y)),...
    0,0];
endfunction
function [df]=dfsub(x, z)
    df = [(v-z(3)-z(4))/x + z(3)/(x-1) + z(4)/(x-y),...
    -.5*(1/x+1/(x-1)+1/(x-y)),z(1)/(x*(x-1)),z(1)*y/(x*(x-y));...
    0,0,0,0;0,0,0,0];
endfunction

// Boundary conditions

function [g]=gsub(i, z)
    select i
    case 1, g = z(2) - 2*z(1)*(v-z(3)-z(4))
    case 2, g = z(2) - 2*z(1)*z(3)
    case 3, g = z(1)-1.
    case 4, g = z(2) - 2*z(1)*z(4)
    end
endfunction
function [dg]=dgsub(i, z)
        select i
        case 1, dg = [-2*(v-z(3)-z(4)),1.,2*z(1),2*z(1)]
        case 2, dg = [-2*z(3),1.,-2*z(1),0]
        case 3, dg = [1,0,0,0]
        case 4, dg = [-2*z(4),1.,0,-2*z(1)]
        end
endfunction

// Start computation

// Locations of side conditions, sorted
zeta = [0.0d0, 1.0d0, 1.0d0, y];
// Interval ends
aleft = 0.0d0;
aright = y;

// Array of 40 values of v explored by continuation, and array of 202
// points where to evaluate function f.
valv = [linspace(0,.9,10) logspace(0,2,30)];
res = [linspace(0,.99,100) linspace(1,y,101)];

// eigenstates are characterized by number of nodes in [0,1] and in
// [1,y], here guess selects one node (zero) in [0,1] with linear
// f(x)=2*x-1 and constant c_2, c_3, so dmval=0. Notice that the z-vector
// has mstar = 4 components, while dmval has ncomp = 3 components.

function [z, dmval]=guess(x)
     z = [2*x-1, 2., 1., 1/(2*y-1)]
     dmval = [0,0,0]
endfunction

// First execution has ipar(9)=1 and uses the guess
// Subsequent executions have ipar(9)=3 and use continuation. This is
// run in tight closed loop to not disturb the stack

for i = 1:40
    v = valv(i);
    sol = bvode(res,ncomp,m,aleft,aright,zeta,ipar,ltol,tol,fixpnt,...
                fsub,dfsub,gsub,dgsub,guess);
    eigens(:,i) = [v;sol(3,101);sol(4,101)];  // c_2 and c_3 are constant!
    ipar(9) = 3;
end

// To see the evolution of the eigenvalues with v, disp(eigens)
// Note they evolve smoothly.
// To see the solution f for v=40, disp(sol(1,:)). Note that it vanishes
// exactly once in [0,1] at x close to 0.98, and becomes very small
// when x -> 0 and very large when x -> y.
// This is markedly different from the case  at small v.
// The continuation procedure allows to explore these exponential behaviours
// without skipping to other eigenstates.

Used Functions

This function is based on the Fortran routine colnew developed by

U. Ascher, Department of Computer Science, University of British Columbia, Vancouver, B.C. V6T 1W5, Canada

G. Bader, institut f. Angewandte mathematik university of Heidelberg; im Neuenheimer feld 294d-6900 Heidelberg 1

Bibliography

U. Ascher, J. Christiansen and R.D. Russell, collocation software for boundary-value ODEs, acm trans. math software 7 (1981), 209-222. this paper contains EXAMPLES where use of the code is demonstrated.
G. Bader and U. Ascher, a new basis implementation for a mixed order boundary value ode solver, siam j. scient. stat. comput. (1987).
U. Ascher, J. Christiansen and R.D. Russell, a collocation solver for mixed order systems of boundary value problems, math. comp. 33 (1979), 659-679.
U. Ascher, J. Christiansen and R.D. russell, colsys - a collocation code for boundary value problems, lecture notes comp.sc. 76, springer verlag, b. children et. al. (eds.) (1979), 164-185.
C. Deboor and R. Weiss, solveblok: a package for solving almost block diagonal linear systems, acm trans. math. software 6 (1980), 80-87.

Report an issue
<< Differential calculus, Integration	Differential calculus, Integration	dae >>

bvodeS

Syntax

Arguments

Description

Examples

Used Functions

Bibliography

See also