numderivative
approximate derivatives of a function (Jacobian or Hessian)
Syntax
J = numderivative(f, x) J = numderivative(f, x, h) J = numderivative(f, x, h, order) J = numderivative(f, x, h, order, H_form) J = numderivative(f, x, h, order, H_form, Q) [J, H] = numderivative(...)
Arguments
- f
a function or a list, the function to differentiate.
- x
a n-by-1 or 1-by-n vector of doubles, real, the point where to compute the derivatives.
- h
a 1-by-1 or n-by-1 vector of doubles, the step used in the finite difference approximations. If
his not provided, then the default step is computed depending onxand theorder. Ifhis a 1-by-1 matrix, it is expanded to the same size asx.- order
a 1-by-1 matrix of doubles, integer, positive, the order of the finite difference formula (default
order=2). The available values oforderare 1, 2 or 4.- H_form
a string, the form in which the Hessian will be returned (default
H_form="default").The available values are "default", "blockmat" or "hypermat". See the section "The shape of the Hessian" below for details on this option.
- Q
a real matrix of doubles, modifies the directions of differentiation (default is
Q=eye(n,n)). The matrixQis expected to be orthogonal. Q provides the possibility to remove the arbitrariness of using the canonical basis to approximate the derivatives of a function.- J
a m-by-n matrix of doubles, the approximated Jacobian. The row
J(k, :)approximates the gradient offk, fork = 1, 2, ..., m.- H
a matrix of doubles, the approximated Hessian. The elements of
Happroximate the second-order partial derivatives off.
Description
Computes the approximated Jacobian and Hessian matrices of a function with finite differences.
The function f takes as
input argument x, a n-by-1 vector,
and returns y, a m-by-1 vector.
In the following, the k-th component of f
is denoted by fk and the Hessian matrix of
fk is denoted by Hk,
for k = 1, 2, ..., m.
Any optional argument equal to the empty matrix []
is replaced by its default value.
In general, the order=1 formula provides the
largest error (least accurate), the order = 2 formula provides an average
error and the order=4 formula provides the lowest error (most accurate).
However, there are cases for which this is not true: see the section "Accuracy issues" below
for more details on this topic.
The second derivatives are computed by composition of first order derivatives.
The function
The function f must have the following header:
y = f (x)
where
- x
a n-by-1 vector of doubles, the current point
- y
a m-by-1 vector of doubles, the function value
It might happen that the function requires additional arguments to be evaluated.
In this case, we can use the following feature.
The argument f can also be the list (myfun, a1, a2, ...).
In this case, myfun, the first element in the list, must be a function and must
have the header:
y = myfun (x, a1, a2, ...)
a1, a2, ...
are automatically appended as parameters to the call.The shape of the Hessian
The H_form option changes the dimensions of the output argument
H.
This manages the general case where m is different from 1,
that is, when there are several functions to differentiate at the same time.
The possible values of H_form are:
- H_form = "default":
H is a
m-by-(n^2)matrix; in this form, the rowH(k, :)containsHk:H(k, :) == Hk(:)'- H_form = "blockmat":
H is a
(mn)-by-nmatrix: then-by-nHessian matrices of each component offare stacked row-by-row, that is:H == [H1 ; H2 ; ... ; Hm]- H_form = "hypermat":
H is a n-by-n matrix for
m=1, and a n-by-n-by-m hypermatrix otherwise. The matrixH(:, :, k)is the Hessian matrix of the k-th component off, i.e.H(:, :, k) == Hk
Performances
If the problem is correctly scaled, increasing the order of the finite difference formula may reduce
the error of approximation but requires more function evaluations.
The following list presents the number of function evaluations required to
compute the Jacobian depending on the order of the formula and the dimension of x,
denoted by n:
order = 1, the number of function evaluations isn+1,order = 2, the number of function evaluations is2n,order = 4, the number of function evaluations is4n.
Computing the Hessian matrix requires the square of the number of function evaluations, as detailed in the following list.
order = 1, the number of function evaluations is(n+1)^2(total is(n+1)^2+n+1),order = 2, the number of function evaluations is4n^2(total is4n^2+2n),order = 4, the number of function evaluations is16n^2(total is16n^2+4n).
Examples
// The function to differentiate function y=f(x) f1 = sin(x(1)*x(2)) + exp(x(2)*x(3)+x(1)) f2 = sum(x.^3) y = [f1; f2] endfunction // The exact gradient function [g1, g2]=exactg(x) g1(1) = cos(x(1)*x(2))*x(2) + exp(x(2)*x(3)+x(1)) g1(2) = cos(x(1)*x(2))*x(1) + exp(x(2)*x(3)+x(1))*x(3) g1(3) = exp(x(2)*x(3) + x(1))*x(2) g2(1) = 3*x(1)^2 g2(2) = 3*x(2)^2 g2(3) = 3*x(3)^2 endfunction // The exact Hessian function [H1, H2]=exactH(x) H1(1, 1) = -sin(x(1)*x(2))*x(2)^2 + exp(x(2)*x(3)+x(1)) H1(1, 2) = cos(x(1)*x(2)) - sin(x(1)*x(2))*x(2)*x(1) + exp(x(2)*x(3)+x(1))*x(3) H1(1, 3) = exp(x(2)*x(3)+x(1))*x(2) H1(2, 1) = H1(1, 2) H1(2, 2) = -sin(x(1)*x(2))*x(1)^2 + exp(x(2)*x(3)+x(1))*x(3)^2 H1(2, 3) = exp(x(2)*x(3)+x(1)) + exp(x(2)*x(3)+x(1))*x(3)*x(2) H1(3, 1) = H1(1, 3) H1(3, 2) = H1(2, 3) H1(3, 3) = exp(x(2)*x(3)+x(1))*x(2)^2 // H2(1, 1) = 6*x(1) H2(1, 2) = 0 H2(1, 3) = 0 H2(2, 1) = H2(1, 2) H2(2, 2) = 6*x(2) H2(2, 3) = 0 H2(3, 1) = H2(1, 3) H2(3, 2) = H2(2, 3) H2(3, 3) = 6*x(3) endfunction // Compute the approximate Jacobian, the Hessian x = [1; 2; 3]; J = numderivative(f, x) [J, H] = numderivative(f, x) // Compare with exact derivatives [g1, g2] = exactg(x); Jexact = [g1'; g2'] [H1, H2] = exactH(x); Hexact = [H1(:)'; H2(:)'] // Configure the step J = numderivative(f, x, 1.e-1) // Configure the order J = numderivative(f, x, [], 4) // Configure Hessian shapes [J, H] = numderivative(f, x, [], [], "blockmat") [J, H] = numderivative(f, x, [], [], "hypermat") // Configure Q n = 3; Q = qr(rand(n, n)) J = numderivative(f, x, [], [], [], Q) // Test order 1, 2 and 4 formulas. // For the order 4 formula, there are some entries in H // which are computed as nonzero. [g1, g2] = exactg(x); [H1, H2] = exactH(x); Jexact = [g1'; g2']; Hexact = [H1(:)'; H2(:)']; for i = [1, 2, 4] [J, H] = numderivative(f, x, [], i); dJ = floor(min(assert_computedigits(J, Jexact))); dH = floor(min(assert_computedigits(H, Hexact))); mprintf("order = %d, dJ = %d, dH = %d \n", i, dJ, dH); end
Passing extra parameters
In the following example, we use a function which requires the extra-argument
p.
Hence, we use the feature that the argument f
can be a list, where the first argument is the function
G and the remaining elements are automatically passed
to the function.
The Taylor formula
If H is given in its default form, then the Taylor series of
f(x) up to terms of second order is given by:
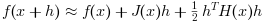
In the following script, we check this formula with numerical differences.
// The function to differentiate function y=f(x) f1 = sin(x(1)*x(2)) + exp(x(2)*x(3)+x(1)) f2 = sum(x.^3) y = [f1; f2] endfunction x = [1; 2; 3]; dx = 1e-3*[1; 1; -1]; [J, H] = numderivative(f, x); f(x+dx) f(x+dx)-f(x) f(x+dx)-f(x)-J*dx f(x+dx)-f(x)-J*dx-1/2*H*(dx .*. dx)
In the following example, we use a function which requires three extra-arguments
A, p and w.
Accuracy issues
When the step h is not provided, the numderivative
function tries to compute a step which provides a sufficient accuracy.
This step depends on the degree of the derivative (Jacobian or Hessian),
the order of the formula and the point x.
More precisely, if x is nonzero,
then the default step h is a vector with the
same size as x, scaled with the absolute value
of x.
In the following example, we compute the derivative of the square root function. The following script plots a graph which represents the relative error of the numerical derivative depending on the step. We can see that there is an optimal step which minimizes the relative error.
// Its exact derivative function y=mydsqrt(x) y = 0.5 * x^(-0.5) endfunction x = 1.0; n = 1000; logharray = linspace (-16, 0, n); for i = 1:n h = 10^(logharray(i)); expected = mydsqrt(x); computed = numderivative (sqrt, x, h); relerr = abs(computed - expected) / abs(expected); logearray (i) = log10 (relerr); end scf(); plot (logharray, logearray); xtitle("Relative error of numderivative (x = 1.0)", .. "log(h)", "log(RE)");
The strategy in numderivative provides a sufficient accuracy in many
cases, but can fail to be accurate in some cases.
In fact, the optimal step also depends on the function value f(x)
and is second derivative, both of which are unknown at the time where the
default step is computed.
See "Practical optimization", by Gill, Murray and Wright, Academic Press, 1981,
for more details on this topic.
The relevant sections are "4.6.1. Finite-difference Approximations to First
Derivatives" and "8.6 Computing finite differences".
History
| Version | Description |
| 5.5.0 | Function numderivative introduced. |
| Report an issue | ||
| << inttrap | Differential calculus, Integration | ode >> |