rpem
Recursive Prediction-Error Minimization estimation
Syntax
[w1,[v]]=rpem(w0,u0,y0,[lambda,[k,[c]]])
Arguments
- w0
list(theta,p,l,phi,psi)where:- theta
[a,b,c] is a real vector of order
3*n- a,b,c
a=[a(1),...,a(n)], b=[b(1),...,b(n)], c=[c(1),...,c(n)]
- p
(3*n x 3*n) real matrix.
- phi,psi,l
real vector of dimension
3*n
Applicable values for the first call:
- u0
real vector of inputs (arbitrary size). (
u0($)is not used by rpem)- y0
vector of outputs (same dimension as
u0). (y0(1)is not used by rpem).If the time domain is
(t0,t0+k-1)theu0vector contains the inputsu(t0),u(t0+1),..,u(t0+k-1)andy0the outputsy(t0),y(t0+1),..,y(t0+k-1)
Optional arguments
- lambda
optional argument (forgetting constant) chosen close to 1 as convergence occur:
lambda=[lambda0,alfa,beta]evolves according to :lambda(t)=alfa*lambda(t-1)+beta
with
lambda(0)=lambda0- k
contraction factor to be chosen close to 1 as convergence occurs.
k=[k0,mu,nu]evolves according to:k(t)=mu*k(t-1)+nu
with
k(0)=k0.- c
Large argument.(
c=1000is the default value).
Outputs:
- w1
Update for
w0.- v
sum of squared prediction errors on
u0, y0.(optional).In particular
w1(1)is the new estimate oftheta. If a new sampleu1, y1is available the update is obtained by:[w2,[v]]=rpem(w1,u1,y1,[lambda,[k,[c]]]). Arbitrary large series can thus be treated.
Description
Recursive estimation of arguments in an ARMAX model. Uses Ljung-Soderstrom recursive prediction error method. Model considered is the following:
y(t)+a(1)*y(t-1)+...+a(n)*y(t-n)= b(1)*u(t-1)+...+b(n)*u(t-n)+e(t)+c(1)*e(t-1)+...+c(n)*e(t-n)
The effect of this command is to update the estimation of
unknown argument theta=[a,b,c] with
a=[a(1),...,a(n)], b=[b(1),...,b(n)], c=[c(1),...,c(n)].
Example
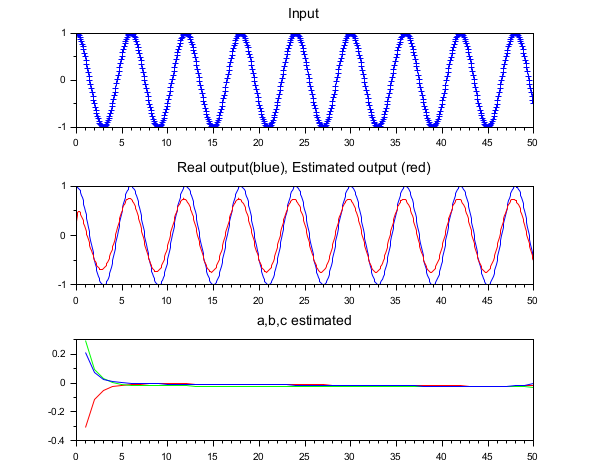
nbPoints = 50; // Number of points computed // Real parameters a,b,c: here, y=u a=cat(2,1,zeros(1,nbPoints - 1)); b=cat(2,1,zeros(1,nbPoints - 1)); c=zeros(1,nbPoints); // Generate input signal t=linspace(0,50,600); w=%pi/3; u=cos(w*t); // Generate output signal Arma=armac(a,b,c,1,1,0); y=arsimul(Arma,u); f1=figure("figure_name","figure1","backgroundColor",[1 1 1]); subplot(3,1,1); plot(t, u, "b+"); xtitle("Input"); subplot(3,1,2); plot(t, y); // Arguments of rpem phi=zeros(1,nbPoints*3); psi=zeros(1,nbPoints*3); l=zeros(1,nbPoints*3); p=1*eye(nbPoints*3,nbPoints*3); theta=[0*a 0*b 0*c]; w0=list(theta,p,l,phi,psi); [w0, v]=rpem(w0,u,y); // Get estimated parameters: a_est=w0(1)(1); b_est=w0(1)(nbPoints + 1); c_est=w0(1)(2 * nbPoints + 1); for i=2:nbPoints a_est=cat(2,a_est,w0(1)(i)); b_est=cat(2,b_est,w0(1)(i+nbPoints)); c_est=cat(2,c_est,w0(1)(i+2*nbPoints)); end // Generate and plot output estimated Arma_est=armac(a_est,b_est,c_est,1,1,0); y_est=arsimul(Arma_est,u); plot(t, y_est,"color","red"); xtitle("Real output(blue), Estimated output (red)"); // Plot estimated parameters subplot(3,1,3); xtitle("a,b,c estimated"); plot(a_est(1,:),"color","red"); plot(b_est(1,:),"color","green"); plot(c_est(1,:),"color","blue");
| Report an issue | ||
| << phc | Identification | Spectral estimation >> |