Please note that the recommended version of Scilab is 2026.0.1. This page might be outdated.
See the recommended documentation of this function
Implicit Runge-Kutta 4(5)
Solveur numérique fournissant une méthode implicite efficace et stable pour résoudre des Problèmes à Valeur Initiale d'Equations Différentielles Ordinarires (EDOs)
Description
Runge-Kutta est un solveur numérique fournissant une méthode explicite efficace pour résoudre des Problèmes à Valeur Initiale de la forme :
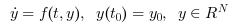
CVode et IDA utilisent un pas variable dans l'intégration.
Le défaut de cela est l'imprévisibilité du temps de calcul. Avec Runge-Kutta, on ne s'adapte pas à la complexité du problème, mais on garantit un temps de calcul stable.
Cette méthode étant implicite, elle peut être utilisée sur des problèmes raides.
C'est une amélioration de la méthode d'Euler implicite, qui approxime yn+1 en calculant f(tn+h, yn+1) et tronquant le développement de Taylor.
Le schéma implémenté est inspiré de "Low-Dispersion Low-Dissipation Implicit Runge-Kutta Scheme" (lien en bas de page).
Par convention, pour utiliser des pas fixes, le programme commence par calculer un pas h qui approche le paramère de simulation max step size.
Une différence notable de Runge-Kutta implicite par rapport à Sundials est qu'il calcule jusqu'à la dérivée quatrième de y, alors que les autres n'utilisent que des combinaisons linéaires de y et y'.
Ici, la valeur suivante yn+1 est déterminée par la valeur actuelle yn plus la moyenne pondérée de trois increments, où chaque incrément est le produit du pas, h, et une estimation de la pente spécifiée par la fonction f(t,y). Ils sont distribués de manière à peu près égale sur l'intervalle.
- k1 est l'incrément basé sur la pente au début de l'intervalle, utilisant yn+ a11*h*k1, ,
- k2 est l'incrément basé sur la pente près du milieu de l'intervalle, utilisant yn + a21*h*k1 + a22*h*k2, ,
- k3 est l'incrément basé sur la pente trois quarts de l'intervalle, utilisant yn + a31*h*k1 + a32*h*k2 + a33*h*k3.
On peut voir que le calcul d'un ki requiert ki, nécéssitant ainsi l'utilisation d'un solveur non linéraire (ici, itérations point-fixes).
D'abord, on initialise k0 = h * f(tn, yn) comme première estimation pour tous les ki, pour obtenir de nouveaux ki et une première valeur pour yn+1 .
Ensuite, on sauve les valeurs et on recalcule yn+1 avec ces nouveaux ki.
Puis on compare les deux yn+1 et on le recalcule jusqu'à ce que son écart avec le dernier soit inférieur au paramètre de simulation reltol.
Ce processus ajoute un temps de calcul significatif à la méthode, mais améliore grandement la stabilité.
On peut voir qu'avec les ki, on progresse dans les dérivées de yn . Donc avec k3, on approxime y(3)n , faisant donc une erreur en O(h4) . Mais un choix judicieux des coefficients du calcul des ki (notamment aij ) nous fait gagner un ordre, produisant ainsi une erreur par pas de temps en O(h5) .
L'erreur totale est donc nombre de pas * O(h5) . Et puisque par définition nombre de pas = taille de l'intervalle / h, l'erreur totale est en O(h4) .
Cette analyse d'erreur a baptisé la méthode Runge-Kutta Implicite 4(5): O(h5) par pas, O(h4) au total.
Bien que le solveur fonctionne bien pour max step size jusqu'à 10-3 , les erreurs d'arrondi surviennent parfois quand l'on approche 4*10-4 . En effet, le scindage de l'intervalle ne peut pas être effectué correctement et l'on obtient des résultats imprévisibles.
Examples
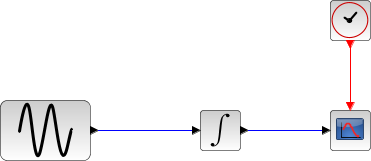
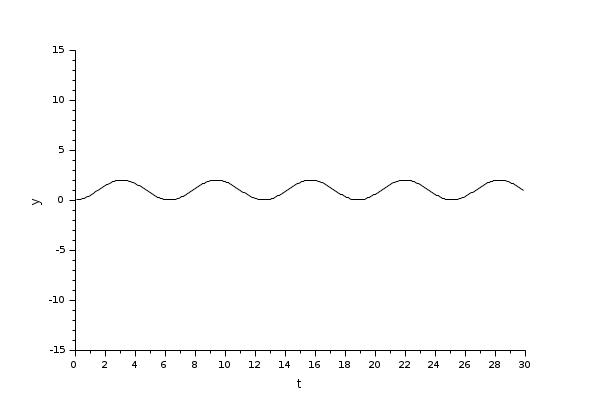
Le bloc intégrale retourne son état continu, on peut l'évaluer avec RK implicite en lançant l'exemple :
// Import du diagramme et réglage du temps final loadScicos(); loadXcosLibs(); importXcosDiagram("SCI/modules/xcos/examples/solvers/ODE_Example.zcos"); scs_m.props.tf = 5000; // Sélection de RK implicite et réglage de la précision scs_m.props.tol(2) = 10^-10; scs_m.props.tol(6) = 7; scs_m.props.tol(7) = 10^-2; // Lancement du chrono, de la simulation et affichage du temps tic(); try xcos_simulate(scs_m, 4); catch disp(lasterror()); end t = toc(); disp("Temps pour Runge-Kutta implicite :", t);
La console Scilab affiche :
Temps pour Runge-Kutta implicite :
8.911
Maintenant, dans le script suivant, on compare la différence de temps entre RK implicite et CVode en lançant l'exemple avec les cinq solveurs tour à tour : Ouverture du script
Temps pour BDF / Newton :
18.894
Temps pour BDF / Functional :
18.382
Temps pour Adams / Newton :
10.368
Temps pour Adams / Functional :
9.815
Temps pour Runge-Kutta implicite :
6.652
Ces résultats montrent que pour un problème non-raide, pour à peu près la même précision demandée et en forçant la même taille de pas, RK implicite est plus rapide.
Voir Aussi
- LSodar — LSodar (abréviation de "Livermore Solver for Ordinary Differential equations, with Automatic method switching for stiff and nonstiff problems, and with Root-finding") est un solveur numérique fournissant une méthode efficace et stable pour résoudre des Problèmes à Valeur Initiale d'Equations Différentielles Ordinaires (EDOs).
- CVode — CVode (abréviation de "C-language Variable-coefficients ODE solver") est un solveur numérique fournissant une méthode efficace et stable pour résoudre des Problèmes à Valeur Initiale d'Equations Différentielles Ordinarires (EDOs). Il utilise BDF ou Adams comme méthode d'intégration, et des itérations fonctionnelles ou de Newton.
- IDA — "Implicit Differential Algebraic equations system solver" est un solveur numérique fournissant une méthode efficace et stable pour résoudre des Problèmes à Valeur Initiale d'Equations Différentielles Algebriques (EDAs).
- Runge-Kutta 4(5) — Runge-Kutta est un solveur numérique fournissant une méthode explicite efficace pour résoudre des Problèmes à Valeur Initiale d'Equations Différentielles Ordinarires (EDOs).
- Dormand-Prince 4(5) — Dormand-Prince est un solveur numérique fournissant une méthode explicite efficace pour résoudre des Problèmes à Valeur Initiale d'Equations Différentielles Ordinarires (EDOs).
- Crank-Nicolson 2(3) — Crank-Nicolson est un solveur numérique basé sur le schéma Runge-Kutta fournissant une méthode implicite efficace et stable pour résoudre des Problèmes à Valeur Initiale d'Equations Différentielles Ordinaires (EDOs). Appelé par xcos.
- DDaskr — "Double-precision Differential Algebraic equations system Solver with Krylov method and Rootfinding" : solveur numérique fournissant une méthode efficace et stable pour résoudre des Problèmes à Valeur Initiale d'Equations Différentielles Algebriques (EDAs).
- Comparaisons — Cette page compare les solveurs pour déterminer lequel est le mieux adapté au le problème étudié.
- ode_discrete — ordinary differential equation solver, discrete time simulation
- ode_root — ordinary differential equation solver with roots finding
- odedc — discrete/continuous ode solver
- impl — differential algebraic equation
Bibliographie
Journal of Computational Physics, Volume 233, Janvier 2013, Pages 315-323 A low-dispersion and low-dissipation implicit Runge-Kutta scheme
Histoire
| Version | Description |
| 5.4.1 | Runge-Kutta Implicite 4(5) ajouté |
| Report an issue | ||
| << Dormand-Prince 4(5) | Solveurs | Crank-Nicolson 2(3) >> |